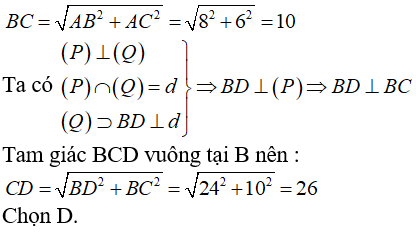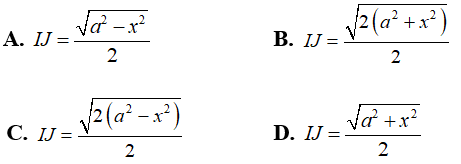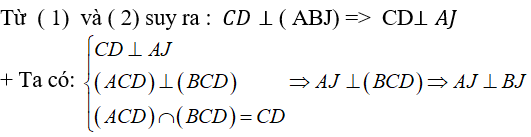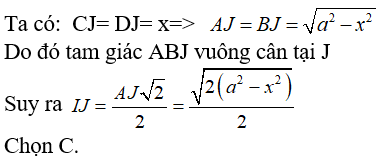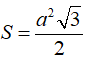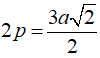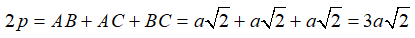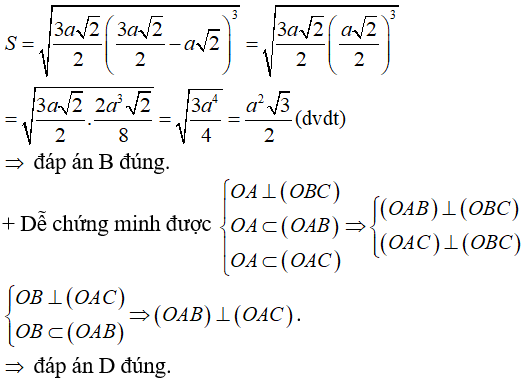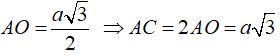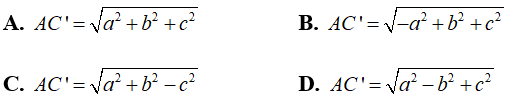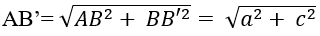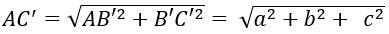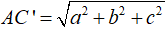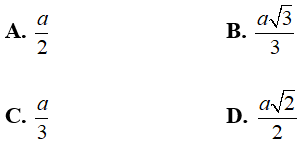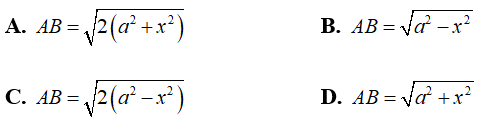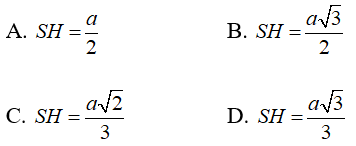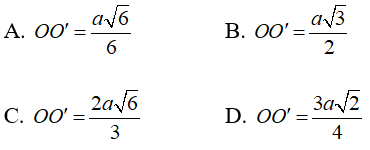Cách tính độ dài đoạn thẳng trong không gian cực hay

B. Ví dụ minh họa

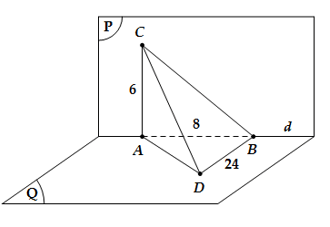
Ví dụ 1: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Người ta lấy trên giao tuyến d của hai mặt phẳng đó hai điểm A và B sao cho AB= 8. Gọi C là một điểm trên (P) , D là một điểm trên (Q) sao cho AC; BD cùng vuông góc với giao tuyến d và AC = 6; BD = 24. Độ dài CD là:

A. 20           B. 22           C. 30           D. 26

Hướng dẫn giải:

Tam giác ABC vuông tại A nên

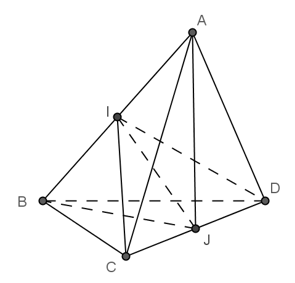
Ví dụ 2: Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a; CD = 2x. Gọi I và J lần lượt là trung điểm của AB và CD. Tính IJ theo a và x?

Hướng dẫn giải:

+ Tam giác ACD cân tại A có AJ đường trung tuyến nên đồng thời là đường cao: AJ ⊥ CD  (1)

Tam giác BCD cân tại B có BJ là đường trung tuyến nên đồng thời là đường cao : BJ ⊥ CD  (2)

Vậy tam giác ABJ vuông tại J

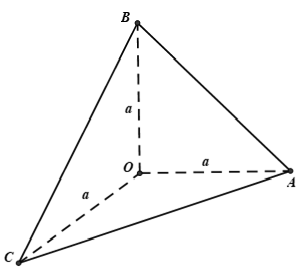
Ví dụ 3: Cho ba tia Ox, Oy, Oz vuông góc nhau từng đôi một. Trên Ox, Oy, Oz lần lượt lấy các điểm A, B, C sao cho OA = OB = OC = a. Khẳng định nào sau đây sai?

A. O.ABC là hình chóp đều

B. Tam giác ABC có diện tích 

C. Tam giác ABC có chu vi 

D. Ba mặt phẳng (OAB), (OBC) và (OAC) vuông góc với nhau từng đôi một.

Hướng dẫn giải:

Chọn C

+ Áp dụng định lý Pytago trong tam giác OAB vuông tại O ta có:

AB² = OA² + OB² = a² + a² = 2a² ⇒ AB = a√2

Hoàn toàn tương tự ta tính được BC = AC = a√2.

⇒ Tam giác ABC là tam giác đều.

Mặt khác theo giả thiết OA = OB = OC = a

⇒ Các mặt bên của hình chóp O. ABC là các tam giác cân tại O còn đáy ABC là tam giác đều

⇒ O.ABC là hình chóp đều ⇒ phương án A đúng.

+ Chu vi tam giác BAC là:

⇒ phương án C sai

+ Nửa chu vi tam giác ABC là: p = 3a(√2)/2 .

Áp dụng công thức Hê - rông, diện tích tam giác ABC là:

Chọn C

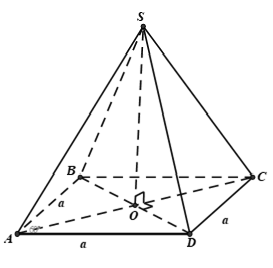
Ví dụ 4: Cho hình thoi ABCD có cạnh bằng a và ∠A = 60° . Trên đường thẳng vuông góc với mặt phẳng (ABDC) tại O (O là tâm của ABCD), lấy điểm S sao cho tam giác SAC là tam giác đều. Khẳng định nào sau đây đúng?

A. S.ABCD là hình chóp đều.

B. Hình chóp S.ABCD có các mặt bên là các tam giác cân.

C. SO = 3a/2

D. SA và SB hợp với mặt phẳng (ABCD) những góc bằng nhau.

Hướng dẫn giải:

Chọn C

+ Xét tam giác ABD có ∠ = 60° và AB = AD = a

⇒ tam giác ABD là tam giác đều cạnh a.

+ Vì O là tâm của ABCD nên suy ra AO là đường trung tuyến trong tam giác ABD đều cạnh a nên tính được

+ Mặt khác theo giả thiết SAC là tam giác đều ⇒ SA = SC = AC = a√3

Áp dụng định lí Py ta go vào tam giác SOA ta có:

SO = √(SA² - AO²) = 3a/2

⇒ C đúng

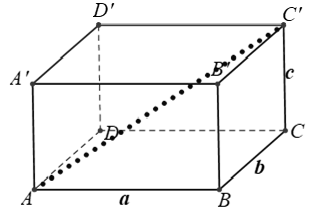
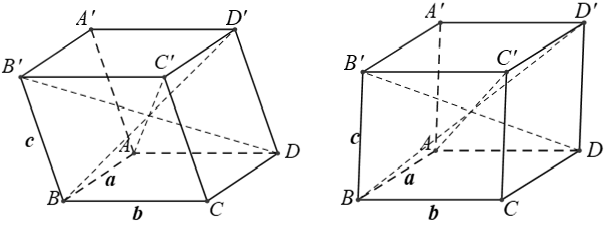
Ví dụ 5: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, CC' = c. Độ dài đường chéo AC' là

Hướng dẫn giải:

Áp dụng định lí Py-ta-go vào tam giác vuông ABB’ ta có :

Do ABCD.A’B’C’D’ là hình lập phương nên:

B’C’ ⊥ (ABB'A') ⇒ B'C ⊥ AB'

Áp dụng định lí Py-ta-go vào tam giác vuông AB’C’ ta có:

Vậy đường chéo hình hộp chữ nhật 

Chọn A

Ví dụ 6: Cho hình hộp ABCD.A'B'C'D' có AB = a, BC = b, CC’ = c. Nếu AC' = BD' = B'D = √(a² + b² + c²) thì hình hộp là

A. Hình lập phương

B. Hình hộp chữ nhật

C. Hình hộp thoi

D. Hình hộp đứng

Hướng dẫn giải:

Nếu AC’= BD’ ⇒ hình bình hành ABC’D’ là hình chữ nhật

Nếu BD’= B’D ⇒ hình bình hành BDD’B’ là hình chữ nhật

Nếu AC’= B’D ⇒ hình bình hành ADC’B’ là hình chữ nhật

⇒ nếu AC’ = BD’ = B’D thì hình hộp là hình hộp chữ nhật.

Chọn B

C. Bài tập vận dụng

Câu 1: Cho hình lăng trụ đứng ABC.A'B'C' có AB = AA’= a, BC = 2a, CA = a√5. Khẳng định nào sau đây sai?

A. Đáy ABC là tam giác vuông

B. Hai mặt (AA’B’B) và (BB’C’) vuông góc nhau.

C. Góc giữa hai mặt phẳng (ABC) và (A’BC) có số đo bằng 45°

D. AC' = 2a√2

Câu 2: Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng a và góc ∠A = 60°, cạnh SC = a√6/2 và SC vuông góc với mặt phẳng (ABCD). Trong tam giác SCA kẻ IK ⊥ SA tại K . Tính độ dài IK được

Câu 3: Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng 2a√3 và cạnh bên bằng 2a. Gọi G và G’ lần lượt là trọng tâm của hai đáy ABC và A’B’C’. Khẳng định nào sau đây đúng khi nói về AGG’A’?

A. AA'G'G là hình chữ nhật có hai kích thước là 2a và 3a.

B. AA'G'G là hình vuông có cạnh bằng 2a.

C. AA'G'G là hình chữ nhật có diện tích bằng 6a².

D. AA'G'G là hình vuông có diện tích bằng 8a².

Câu 4: Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a; CD = 2x. Tính AB theo a và x?

Câu 5: Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa một mặt bên và mặt đáy bằng 60°. Tính độ dài đường cao SH.

Câu 6: Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có ACC’A’ là hình vuông, cạnh bằng a. Cạnh đáy của hình lăng trụ bằng:

Câu 7: Cho hình chóp cụt đều ABC.A'B'C' với đáy lớn ABC có cạnh bằng a. Đáy nhỏ A’B’C’ có cạnh bằng a/2 , chiều cao OO' = a/2. Khẳng định nào sau đây sai?

A. Ba đường cao AA’, BB’, CC’ đồng qui tại S.

B. AA' = BB' = CC' = a/2

C. Góc giữa mặt bên mặt đáy là góc SIO ( I là trung điểm BC).

D. Đáy lớn ABC có diện tích gấp 4 lần diện tích đáy nhỏ A’B’C’.

Câu 8: Cho hình lăng trụ lục giác đều ABCD.A'B'C'D' có cạnh bên bằng a và ADD’A’ là hình vuông. Cạnh đáy của lăng trụ bằng:

A. a           B. a/2           C. a√3/3           D. a√2/2

Câu 9: Cho hình chóp cụt tứ giác đều ABCD.A'B'C'D' cạnh của đáy nhỏ ABCD bằng a/3 và cạnh của đáy lớn A'B'C'D' bằng a. Góc giữa cạnh bên và mặt đáy bằng 60° . Tính chiều cao OO’ của hình chóp cụt đã cho.