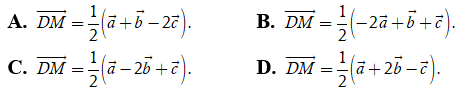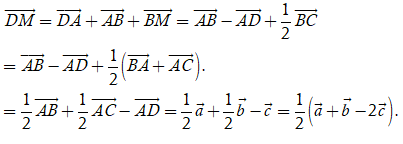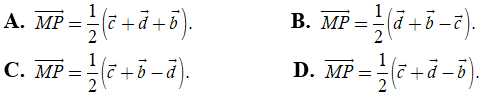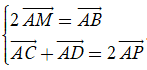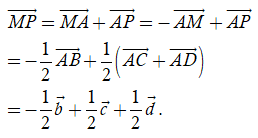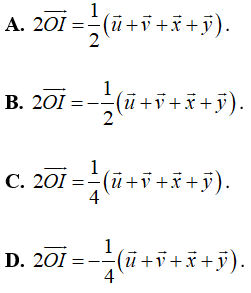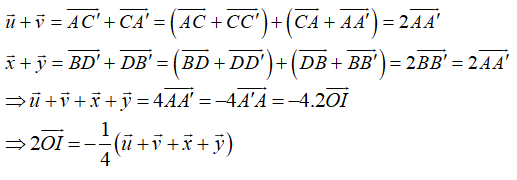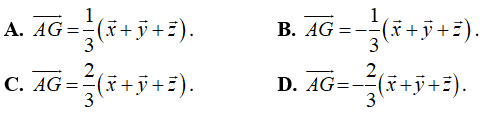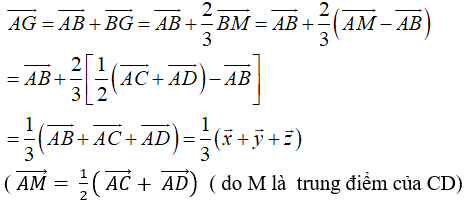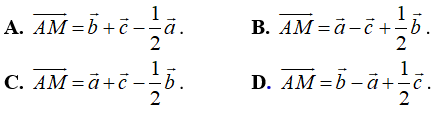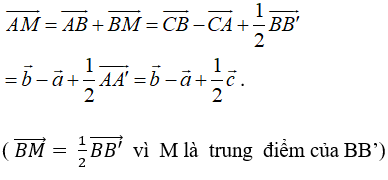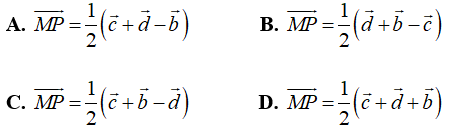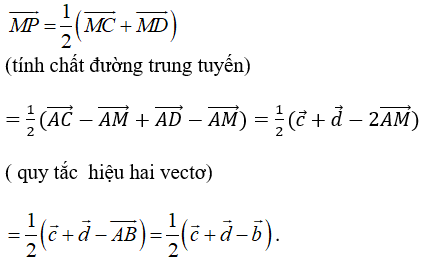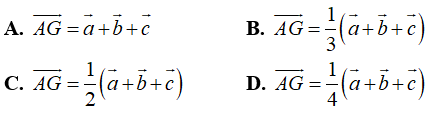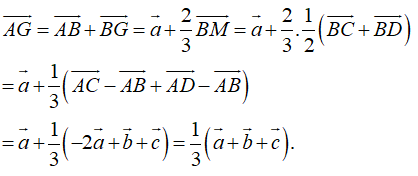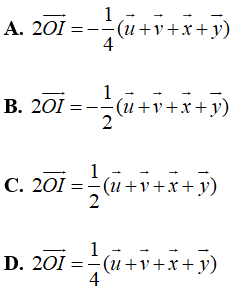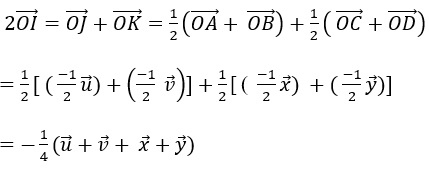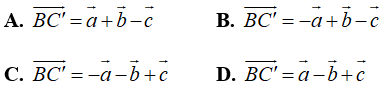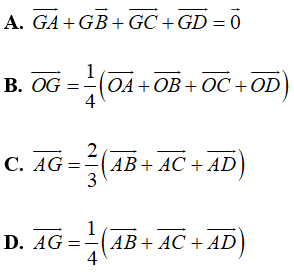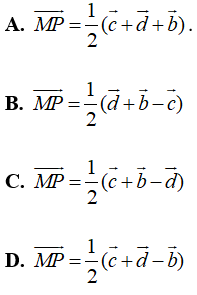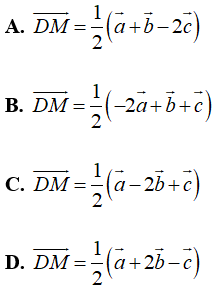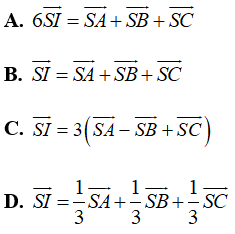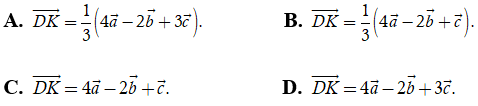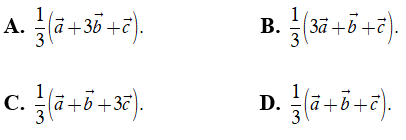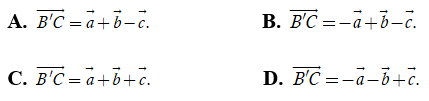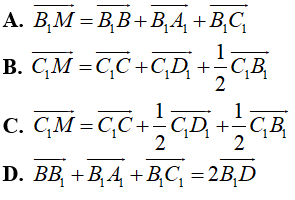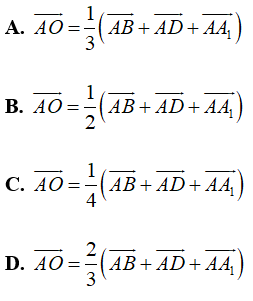Cách phân tích một vectơ theo các vectơ khác hay, chi tiết | Biểu diễn 1 vectơ theo 2, 3 vectơ không cùng phương

A. Phương pháp giải

* Sử dụng các quy tắc ba điểm, quy tắc hình bình hành, quy tắc hình hộp và

trung điểm đoạn thẳng...

B. Ví dụ minh họa

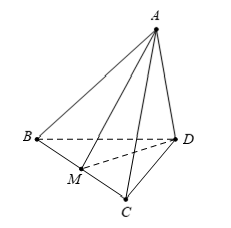
Ví dụ 1: Cho tứ diện ABCD. Đặt . Gọi M là trung điểm của đoạn thẳng BC. Đẳng thức nào dưới đây là đúng?

Hướng dẫn giải:

Vì M là trung điểm của BC suy ra $\overrightarrow{BM}$ = (1/2).$\overrightarrow{BC}$

Ta có

Chọn A

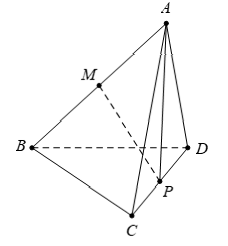
Ví dụ 2: Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt . Khẳng định nào sau đây là đúng?

Hướng dẫn giải:

Vì M; P lần lượt là trung điểm của AB; CD ⇒ 

Ta có:

Chọn D

Ví dụ 3: Cho hình hộp ABCD. A’B’C’D’ có tâm O. Gọi I là tâm hình bình hành ABCD. Đặt . Khẳng định nào sau đây đúng?

Hướng dẫn giải:

Chọn D.

Áp dụng quy tắc 3 điểm : AB→ + BC→ = AC→ ta được :

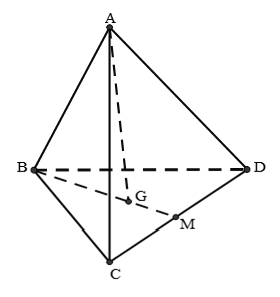
Ví dụ 4: Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Đặt . Khẳng định nào sau đây đúng?

Hướng dẫn giải:

Chọn A

Gọi M là trung điểm CD

Ta có :

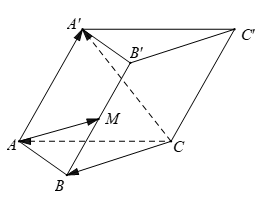
Ví dụ 5: Cho hình lăng trụ ABC.A’B’C’ gọi M là trung điểm của BB’. Đặt  . Khẳng định nào sau đây đúng?

Hướng dẫn giải:

Chọn D

Áp dụng quy tắc 3 điểm và quy tắc hiệu hai vecto ta có :

Ví dụ 6: Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. . Khẳng định nào sau đây đúng?

Hướng dẫn giải:

Chọn A.

Ta phân tích:

Ví dụ 7: Cho tứ diện ABCD. Đặt , gọi G là trọng tâm của tam giác BCD. Trong các đẳng thức sau, đẳng thức nào đúng?

Hướng dẫn giải:

Chọn B.

Gọi M là trung điểm BC. Ta có:

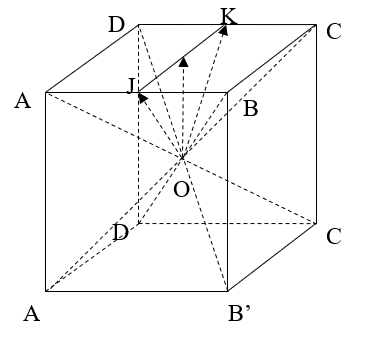
Ví dụ 8: Cho hình hộp ABCD.A’B’C’D’ có tâm O. Gọi I là tâm hình bình hành ABCD. Đặt . Trong các đẳng thức sau, đẳng thức nào đúng?

Hướng dẫn giải:

Chọn A.

+ Gọi J; K lần lượt là trung điểm của AB; CD.

+ Ta có:

C. Bài tập vận dụng

Câu 1: Cho lăng trụ tam giác ABC.A’B’C’ có . Hãy phân tích (biểu thị) vectơ $\overrightarrow{BC\text{'}}$ qua các vectơ .

Câu 2: Cho hình tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây là sai?

Câu 3: Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt . Khẳng định nào sau đây đúng.

Câu 4: Cho tứ diện ABCD. Đặt  gọi M là trung điểm của BC. Trong các khẳng định sau, khẳng định nào đúng?

Câu 5: Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ: 

A. k = (1/2)                    B. k = (1/3)                    C. k = 3                    D. k = 2

Câu 6: Cho tứ diện ABCD và I là trọng tâm tam giác ABC. Đẳng thức đúng là.

Câu 7: Cho hình hộp ABCD.A’B’C’D’ có . Gọi I là trung điểm của B’C’; K là giao điểm của A’I và B’D’. Mệnh đều nào sau đây đúng ?

Câu 8: Cho hình lăng trụ ABC.A’B’C’. Đặt . Gọi G’ là trọng tâm của tam giác A’B’C’. Vectơ $\overrightarrow{AG\text{'}}$ bằng:

Câu 9: Cho hình lăng trụ ABC.A’B’C’. . Hãy biểu diễn vectơ B'C→ theo các vectơ 

Câu 10: Cho hình hộp ABCD.A1B1C1D1. Gọi M là trung điểm AD. Chọn đẳng thức đúng.

Câu 11: Cho hình lập phương ABCD.A1B1C1D1. Gọi O là tâm của hình lập phương. Chọn đẳng thức đúng?