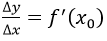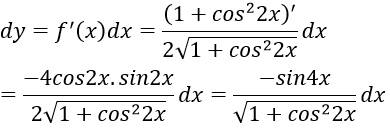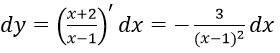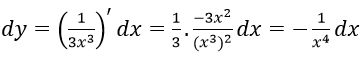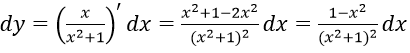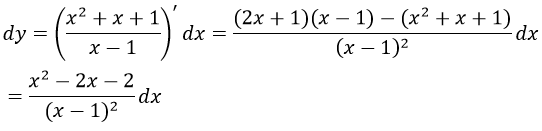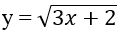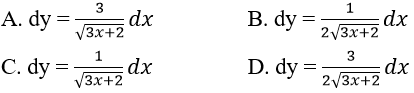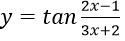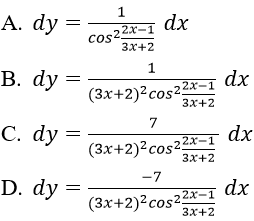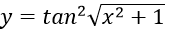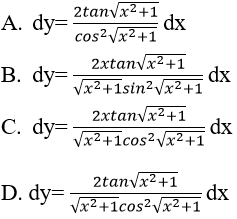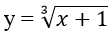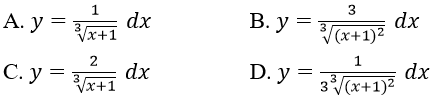Cách tìm vi phân của hàm số hay, chi tiết

A. Phương pháp giải & Ví dụ

Cho hàm có y = f(x) xác định trên (a; b) và có đạo hàm tại x ∈ (a; b). Giả sử Δx là số gia của x sao cho x + Δx ∈ (a; b)

Tích f '(x)Δx(hay y 'Δx) được gọi là vi phân của hàm số f(x) tại x, ứng với số gia Δx, kí hiệu là df(x) hay dy

Chú ý. Vì dx = Δx nên:

      dy = df(x) = f '(x)dx

Ứng dụng vi phân vào phép tính gần đúng

Với |Δx| đủ nhỏ, ta có 

hay Δy = f(x₀ + Δx) - f(x₀) = f '(x₀)Δx

Do đó f(x₀ + Δx) ≈ f(x₀) + f '(x₀)Δx ≈ f(x₀) + df(x₀)

Ví dụ minh họa

Bài 1: Xét hàm số y = 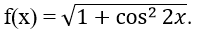Tính vi phân của hàm số đó.

Hướng dẫn:

Ta có :

Bài 2: Cho hàm số 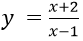.Tính vi phân của hàm số đó.

Hướng dẫn:

Ta có

Bài 3: Cho hàm số y = sinx – 3cosx. Tính vi phân của hàm số.

Hướng dẫn:

Ta có dy = (sinx – 3cosx)’dx = (cosx + 3sinx)dx

Bài 4: Cho hàm số y = x³ - 5x + 6. Tính vi phân của hàm số đó.

Hướng dẫn:

Ta có

dy =(x³-5x+6)'dx = (3x²-5)dx

Bài 5: Cho hàm số y = 1/(3x³). Tính vi phân của hàm số đó

Hướng dẫn:

Ta có

Bài 6: Cho hàm số 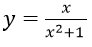. Tính vi phân của hàm số đó.

Hướng dẫn:

Ta có

Bài 7: Cho hàm số 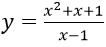. Tính vi phân của hàm số đó

Hướng dẫn:

Ta có

B. Bài tập vận dụng

Bài 1: Cho hàm số f(x) = x² - x + 2. Tính Δf(1) và df(1)nếu Δx = 0,1

A. Δf(1) = 0,11; df(1) = 0,2

B. Δf(1) = 0,11; df(1) = 0,1

C. Δf(1) = 0,2; df(1) = 0,11

D. Δf(1) = 0,2; df(1) = 0,1

Bài 2: Tìm vi phân của hàm số y = (2x+1)⁵

A. dy = 10(2x+1)⁴

B. dy = 5(2x+1)⁴ dx

C. dy = (2x+1)⁴ dx

D. dy = 10(2x+1)⁴ dx

Bài 3: Tìm vi phân của các hàm số y = x³ + 2x²

A. dy = (3x²-4x)dx

B. dy = (3x²+x)dx

C. dy = (3x²+2x)dx

D. dy = (3x²+4x)dx

Bài 4: Tìm vi phân của các hàm số 

Bài 5: Cho hàm số y = x³ - 9x² + 12x - 5. Vi phân của hàm số là:

A. dy = (3x²-18x+12)dx

B. dy = (-3x²-18x+12)dx

C. dy = -(3x²-18x+12)dx

D. dy = (-3x²+18x-12)dx

Bài 6: Tìm vi phân của hàm số 

Bài 7: Tìm vi phân của hàm số y = xsinx + cosx

A. dy = xcosxdx

B. dy = xcosx

C. dy = (2sinx + xcosx)dx

D. dy = (sinx+cosx)dx

Bài 8: Tìm vi phân của hàm số 

Bài 9: Tính vi phân của hàm số y = sin³(2x+1)

A. dy = 3sin²(2x+1)cos⁡(2x+1)dx

B. dy = -6sin²(2x+1)cos⁡(2x+1)dx

C. dy = 6sin²(2x+1)cos⁡(2x+1)dx

D. dy = 3sin²(2x+1)cos⁡(2x+1)dx

Bài 10: Tìm vi phân của hàm số y = cos³(1-x)

A. dy = -sin²(1-x)dx

B. dy = 3cos²(1-x).sin⁡(1-x)dx

C. dy = -3cos²(1-x)sin⁡(1-x)dx

D. dy = 3cos²(1-x)dx

Bài 11: Cho hàm số y = f(x) = (x-1)². Biểu thức nào sau đây chỉ vi phân của hàm số f(x)?

A. dy = 2(x – 1)dx

B. dy = (x-1)² dx

C. dy = 2(x – 1)

D. dy = (2x – 1)dx

Bài 12: Tìm vi phân của các hàm số y = (3x+1)¹⁰

A. dy = 10(3x+1)⁹ dx

B. dy = 30(3x+1)¹⁰ dx

C. dy = 9(3x+1)¹⁰ dx

D. dy = 30(3x+1)⁹ dx

Bài 13: Tìm vi phân của các hàm số 

Bài 14: Tìm vi phân của các hàm số y = sin2x + sin³⁡x

A. dy = (cos2x + 3 sin²⁡x cosx)dx

B. dy = (2cos2x + 3 sin²x cosx)dx

C. dy = (2cos2x + sin²⁡x cosx)dx

D. dy = (cos2x + sin²⁡x cosx)dx

Bài 15: Tìm vi phân của các hàm số y = tan2x.

A. dy = (1 + tan²2x)dx

B. dy = (1 - tan²⁡2x)dx

C. dy = 2(1 - tan²⁡2x)dx

D. dy = 2(1 + tan²⁡2x)dx