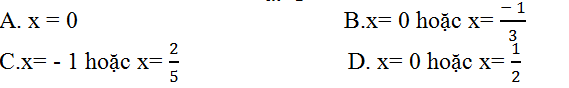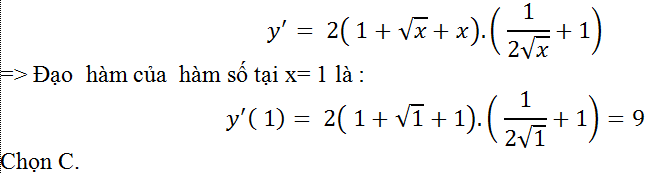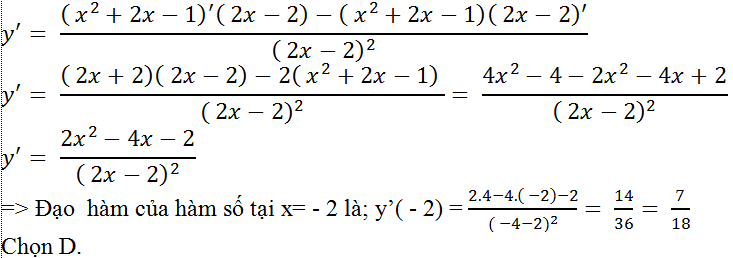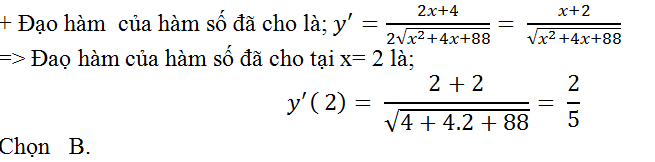Cách tính đạo hàm tại 1 điểm hay, chi tiết

A. Phương pháp giải

Cho hàm số y= f(x). Tính đạo hàm của hàm số tại x= x₀.

+ Bước 1. Tính đạo hàm của hàm số: y’(x)= .....

+ Bước 2. Tính đạo hàm của hàm số tại x₀: thay giá trị x= x₀ vào y’(x); suy ra y’(x₀).

B. Ví dụ minh họa

Ví dụ 1. Cho hàm số y= 16√x+2x- x². Tính đạo hàm của hàm số tại x= 4.

A. – 1        B. – 2        C. 0        D. 2

Hướng dẫn giải

Tại các điểm x > 0 thì hàm số đã cho có đạo hàm và

y'= 8/√x+2-2x

⇒ Đạo hàm của hàm số đã cho tại x= 4 là : y' ( 4)= 8/√4+2-2.4= -2

Chọn B.

Ví dụ 2. Cho hàm số y= (2-2x)/(4x-1). Hỏi tại giá trị x bằng bao nhiêu thì y'= -6?

Hướng dẫn giải

Điều kiện : x≠1/4

Với mọi x thỏa mãn điều kiện; ta có đạo hàm của hàm số là

Ví dụ 3. Cho hàm số y= x³+ mx+ 6. Xác định m biết y' (-2)= 20?

A. m= 8        B. m= - 5        C. m= 6        D. m= - 10

Hướng dẫn giải

Đạo hàm của hàm số đã cho là : y'= 3x²+ m

⇒ y' ( -2 )=12+m

Theo giả thiết ta có: 12+ m= 20 ⇒m= 8

Chọn A.

Ví dụ 4. Cho hàm số y=( 1+ √x+x)². Tính đạo hàm của hàm số tại x= 1?

A. 6        B. 8        C. 9        D. 10

Hướng dẫn giải

+ Với x > 0 thì hàm số đã cho có đạo hàm và

y'=2( 1+√x+x).( 1+ √x+x)'

Ví dụ 5. Cho hàm số y= (x²+2x-1)/(2x-2). Tính đạo hàm của hàm số tại x= - 2

Hướng dẫn giải

Điều kiện : x≠1

Với mọi x≠1 hàm số có đạo hàm là;

Ví dụ 6. Cho hàm số y= √(x²+4x+88). Tính đạo hàm của hàm số đã cho tại x= 2.

A. 1        B. 2/5        C. 1/5        D. 4/5

Hướng dẫn giải

Ta có: x²+ 4x+ 88= ( x+ 2)² + 84 > 0 với mọi x.

⇒ Hàm số đã cho có đạo hàm tại mọi điểm

Ví dụ 7. Cho hàm số y= √(x²-3x+2) + x³- x². Tính đạo hàm của hàm số đã cho tại x= 3/2?

A. 1        B. 2        C. 4        D.không tồn tại

Hướng dẫn giải

+ Điều kiện : x ≤1;x ≥2

+ Tại các điểm x thỏa mãn x2- 3x+ 2 > 0 thì hàm số có đạo hàm .

+ Điểm x= 3/2 không thỏa mãn điều kiện xác định nên hàm số không có đạo hàm tại điểm đó.

Chọn D.

Ví dụ 8. Cho hàm số y= x³+ 2x² – 2x+ 10. Tính đạo hàm của hàm số tại x= 1

A. 5        B. – 2        C. 7        D. 10

Hướng dẫn giải

+ Đạo hàm của hàm số đã cho là : y'= 3x² +4x- 2

⇒ Đạo hàm của hàm số tại điểm x=1 là y' ( 1)= 3. 12+ 4.1- 2= 5

Chọn A.

Ví dụ 9. Cho hàm số y= x²+ 2x- 81. Biết rằng đạo hàm của hàm số tại x= x₀ bằng 4. Tìm x₀?

A. – 2        B. – 1        C. 1        D. 2

Hướng dẫn giải

Đạo hàm của hàm số đã cho là ; y'= 2x+ 2

Theo giả thiết ta có: y' (x₀ )=4 nên 2x₀ + 2= 4

⇔2x₀= 2 ⇔ x₀ = 1

Chọn C.

Ví dụ 10. Cho hàm số y= ( 2x+ x²)². Tính đạo hàm của hàm số tại x= - 1?

A. 0        B. 2        C. – 2        D .4

Hướng dẫn giải

Hàm số đã cho xác định với mọi x.

Đạo hàm của hàm số đã cho là:

y'=2( 2x+ x² )( 2x+ x² )' = 2( 2x+ x² )( 2+2x)

⇒Đạo hàm của hàm số tại x= -1 là y’( - 1) = 0.

Chọn A.

C. Bài tập vận dụng

Câu 1: Cho hàm số y=(2x-6)/(x-8). Hỏi tại giá trị x bằng bao nhiêu thì y'= (- 5)/3?

Câu 2: Cho hàm số y= √(2x²-x-1) + 3x³- 9x. Tính đạo hàm của hàm số đã cho tại x= 0 ?

A. 1        B. 2        C. 0        D.không tồn tại

Câu 3: Cho hàm số y= 2x³+ 3x² + 5x+ 9. Tính đạo hàm của hàm số tại x=- 1

A. 5        B. – 2        C. 7        D. 10

Câu 4: Cho hàm số y= 2x²+ 4x- 1. Biết rằng đạo hàm của hàm số tại x= x₀ bằng 8. Tìm x₀?

A. – 2        B. – 1        C. 1        D. 2

Câu 5: Cho hàm số y= 8√(x+1)+3x- x³. Tính đạo hàm của hàm số tại x= 3.

A. – 12        B. – 18        C. 10        D. - 20

Câu 6: Cho hàm số y= (3+x- 3x²)⁴. Tính đạo hàm của hàm số tại x= 1?

A. -18        B. -20        C. 24        D .4

Câu 7: Cho hàm số y=(x³+ 2√x+x²-1)². Tính đạo hàm của hàm số tại x= 1?

A. 24        B. 18        C. 36        D. 10

Câu 8: Cho hàm số y= 2x³- ( m+ 1)x²+ x+ 1. Xác định m biết y' (2)= 17?

A. m=1        B. m= - 5        C. m= 6        D. m= - 1

Câu 9: Cho hàm số y= (x²+x-6)/(x+3). Tính đạo hàm của hàm số tại x= - 2

A. (- 1)/4        B.1        C. 3/6        D. 2

Câu 10: Cho hàm số y= √(2x²-8x+11). Tính đạo hàm của hàm số đã cho tại x= - 2.