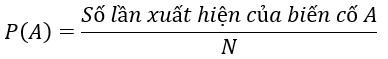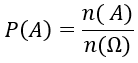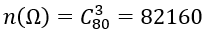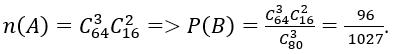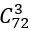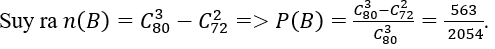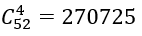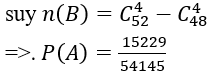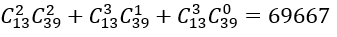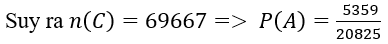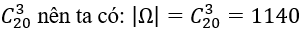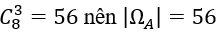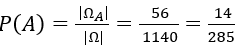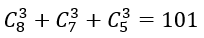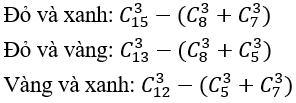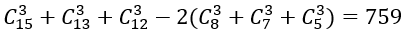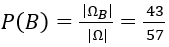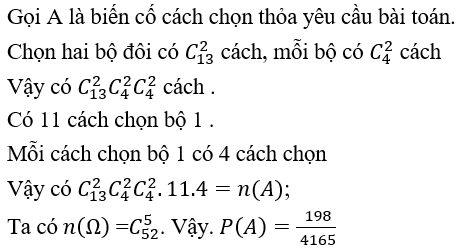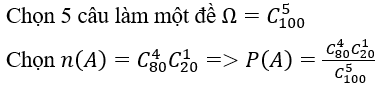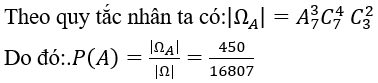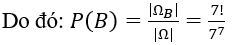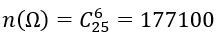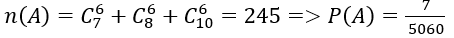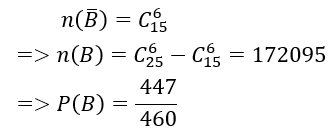Cách tính xác suất theo định nghĩa cổ điển cực hay
Với Cách tính xác suất theo định nghĩa cổ điển cực hay Toán học lớp 11 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách tính xác suất theo định nghĩa cổ điển cực hay.
Cách tính xác suất theo định nghĩa cổ điển cực hay
A. Phương pháp giải & Ví dụ
♦ Tính xác suất theo thống kê ta sử dụng công thức:
♦ Tính xác suất của biến cố theo định nghĩa cổ điển ta sử dụng công thức :
Ví dụ minh họa
Bài 1: Chọn ngẫu nhiên 3 số trong 80 số tự nhiên 1,2,3, . . . ,80
1. Tính xác suất của biến cố A : "trong 3 số đó có và chỉ có 2 số là bội số của 5"
2. Tính xác suất của biến cố B : "trong 3 số đó có ít nhất một số chính phương"
Đáp án và hướng dẫn giải
Số cách chọn 3 số từ 80 số là:
1. Từ 1 đến 80 có số chia hết cho 5 và có số không chia hết cho 5.
Do đó:
2. Từ 1 đến 80 có 8 số chính phương là: 1,4,9,16,25,36,49,64.
Số cách chọn 3 số không có số chính phương nào được chọn là:
Bài 2: Bộ bài tú - lơ khơ có 52 quân bài. Rút ngẫu nhiên ra 4 quân bài. Tìm xác suất của các biến cố:
A: "Rút ra được tứ quý K ‘’
B: "4 quân bài rút ra có ít nhất một con Át"
C: "4 quân bài lấy ra có ít nhất hai quân bích’’
Đáp án và hướng dẫn giải
Ta có số cách chọn ngẫu nhiên 4 quân bài là:
Suy ra n(Ω ) = 270725
Vì bộ bài chỉ có 1 tứ quý K nên ta có n(A)=1
Vậy P(A) = 1 /270725
Vì có 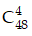
Vì trong bộ bài có 13 quân bích, số cách rút ra bốn quân bài mà trong đó số quân bích không ít hơn 2 là:
Bài 3: Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi. Tìm xác suất để:
1. 3 viên bi lấy ra đều màu đỏ
2. 3 viên bi lấy ra có không quá hai màu.
Đáp án và hướng dẫn giải
Gọi biến cố A :" 3 viên bi lấy ra đều màu đỏ"
B : "3 viên bi lấy ra có không quá hai màu"
Số các lấy 3 viên bi từ 20 viên bi là:
1. Số cách lấy 3 viên bi màu đỏ là:
Do đó:
2. Ta có:
Số cách lấy 3 viên bi chỉ có một màu:
Số các lấy 3 viên bi có đúng hai màu
Nên số cách lấy 3 viên bi có đúng hai màu:
Do đó: |ΩB | = 860. Vậy:

B. Bài tập vận dụng
Bài 1: Chọn ngẫu nhiên 5 quân bài trong cỗ bài tú lơ khơ .Tính xác suất để trong sấp bài chứa hai bộ đôi ( hai con cùng thuộc 1 bộ ,hai con thuộc bộ thứ 2,con thứ 5 thuộc bộ khác )
Lời giải:
Bài 2: Ngân hàng đề thi gồm 100 câu hỏi, mỗi đề thi có 5 câu. Một học sinh học thuộc 80 câu. Tính xác suất để học sinh đó rút ngẫu nhiên được một đề thi có 4 câu học thuộc.
Lời giải:
Bài 3: Một đoàn tàu có 7 toa ở một sân ga. Có 7 hành khách từ sân ga lên tàu, mỗi người độc lập với nhau và chọn một toa một cách ngẫu nhiên. Tìm xác suất của các biến cố sau
A: " Một toa 1 người, một toa 2 người, một toa có 4 người lên và bốn toa không có người nào cả"
B: " Mỗi toa có đúng một người lên".
Lời giải:
Số cách lên toa của 7 người là:.|Ω|=77
1. Tính P(A)=?
Ta tìm số khả năng thuận lợi của A như sau
2. Tính P(B)=?
Mỗi một cách lên toa thỏa yêu cầu bài toán chính là một hoán vị của 7 phần từ nên ta có: |ΩB |=7!
Bài 4: Gieo con súc sắc 100 lần, kết quả thu được ghi ở bảng sau
| Số chấm | Số lần xuất hiện |
| 1 | 14 |
| 2 | 18 |
| 3 | 30 |
| 4 | 12 |
| 5 | 14 |
| 6 | 12 |
Hãy tìm xác suất của các biến cố
A: "mặt sáu chấm xuất hiện"
B: " mặt hai chấm xuất hiện"
C: " một mặt lẻ xuất hiện"
Lời giải:
Xem việc tung con súc sắc là một phép thử ngẫu nhiên
Số lần thực hiện phép thử: N=100
Số lần xuất hiện của biến cố A: 12
Suy ra : P(A)= 12/ 100= 3/ 25
Số lần xuất hiện của biến cố B: 18
Suy ra P(B)= 18/ 100= 9/ 50
Số lần xuất hiện của biến cố C:
Suy ra P(C)= 58/ 100= 29/ 50.
Bài 5: Trong một chiếc hộp có 7 viên bi trắng, 8 viên bi đỏ và 10 viên bi vàng. Lấy ngẫu nhiên ra 6 viên bi
1. Tính số phần tử của không gian mẫu
2. Tính xác suất của các biến cố sau
A: " 6 viên bi lấy ra cùng một màu"
B: " có ít nhất một viên bi màu vàng"
C: " 6 viên bi lấy ra có đủ ba màu"
Lời giải:
1. Ta có:
2. Ta có:
Ta có:
Ta có: Số cách lấy 6 viên bi cùng một màu: 245 cách
Số cách lấy 6 viên bi gồm hai màu:
Suy ra n(C)=177100-35455-245=141400. Vậy P(C)=202/253.