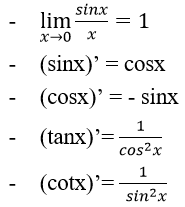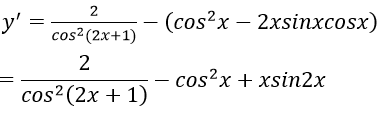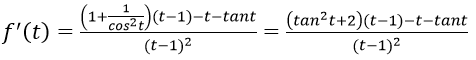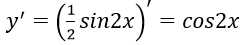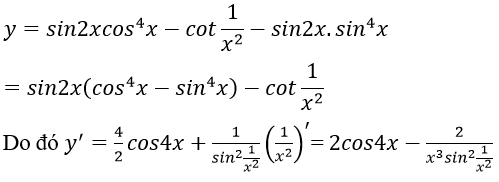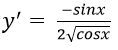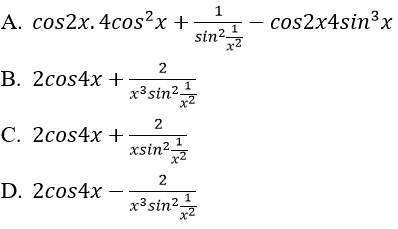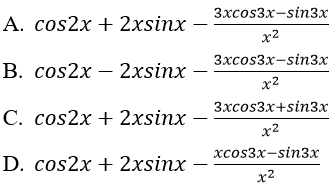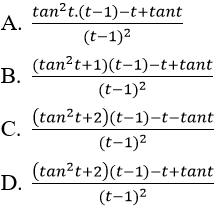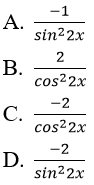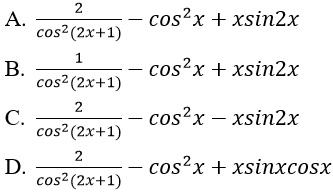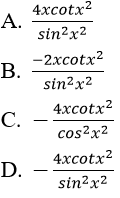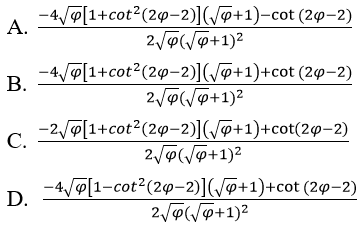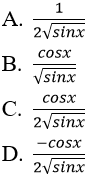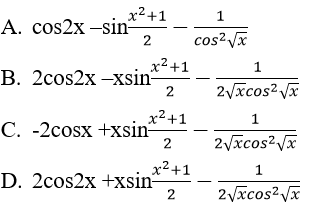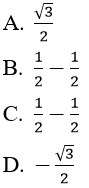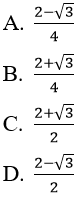Cách tính đạo hàm của hàm số lượng giác cực hay

A. Phương pháp giải & Ví dụ

Ví dụ minh họa

Bài 1: Đạo hàm của hàm số y = tan⁡(2x+1) - xcos²x bằng biểu thức nào?

Hướng dẫn:

Bài 2: Đạo hàm của hàm số 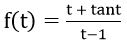bằng biểu thức nào?

Hướng dẫn:

Bài 3: Đạo hàm của hàm số y = 6(sin⁴x + cos⁴x) - 4(sin⁶x + cos⁶x) bằng biểu thức nào?

Hướng dẫn:

y' = 6(sin²x + cos²x)² - 12sin²xcos²x - 4(sin²x + cos²x)² + 12sin²xcos²x(sin²x + cos²x) = 2

Bài 4: Tính đạo hàm của hàm số: y = sinx.cosx

Hướng dẫn:

Bài 5: Đạo hàm của hàm số:

 bằng bao nhiêu?

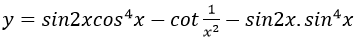
Hướng dẫn:

Bài 6: Tính đạo hàm của hàm số y = cos2x + cos4x + sin5x

Hướng dẫn:

Ta có: y' = -2sin2x - 4sin4x + 5cos5x

Bài 7: Đạo hàm của hàm số y = √cosx bằng biểu thức nào?

Hướng dẫn:

B. Bài tập vận dụng

Bài 1: Đạo hàm của hàm số:

 bằng biểu thức nào sau đây?

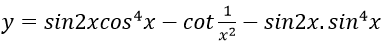
Bài 2: Đạo hàm cuả hàm số:

 bằng biểu thức nào sau đây?

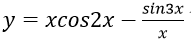
Bài 3: Đạo hàm của hàm số:

 bằng biểu thức nào sau đây?

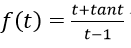
Bài 4: Đạo hàm của hàm số f(x) = cot2x bằng biểu thức nào sau đây?

Bài 5: Đạo hàm cấp hai của hàm số y = cos2x bằng biểu thức nào sau đây?

A. -2sin2x

B. -4cos2x

C. -4sin2x

D. 4cos2x

Bài 6: Đạo hàm của hàm số y = tan⁡(2x+1) - xcos²x bằng biểu thức nào sau đây:

Bài 7: Đạo hàm của hàm số y = cot²x² bằng biểu thức nào sau đây:

Bài 8: Cho hàm số f(x) = sin⁴x + cos⁴x - 2sin²x cos²x. Giá trị của f'(π/24) bằng:

A. -1

B. 1

C. 1/2

D. (-1)/2

Bài 9: Đạo hàm của hàm số:

 bằng biểu thức nào sau đây?

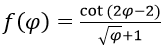
Bài 10: Đạo hàm của hàm số y = 6(sin⁴x + cos⁴x) - 4(sin⁶x + cos⁶x) bằng biểu thức nào sau đây?

A. 24(sin³x + cos³x) - 24(sin⁵x + cos⁵x)

B. 24(sin³x - cos³x) - 24(sin⁵x + cos⁵x)

C. 2

D. 0

Bài 11: Đạo hàm của hàm số y = √sinx bằng biểu thức nào sau đây:

Bài 12: 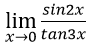 bằng:

A. 1            B. 0            C. 2/3            D. 3/2

Bài 13: Đạo hàm của hàm số:

 bằng biểu thức nào sau đây?

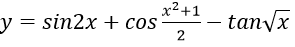
Bài 14: Cho hàm số f(x) = cos²x. Giá trị của f'(π/6) bằng:

Bài 15: Cho hàm số f(x) = sinx.sin2x.sin3x. Giá trị của f'(π/12)bằng: