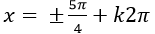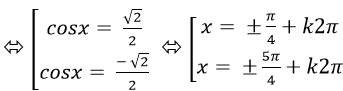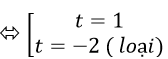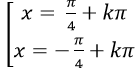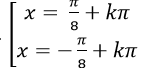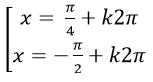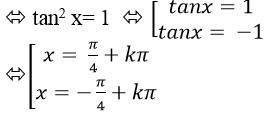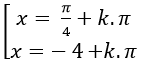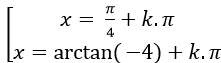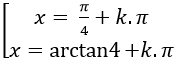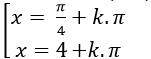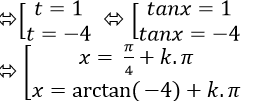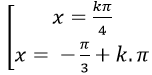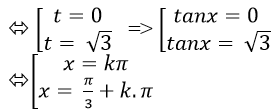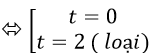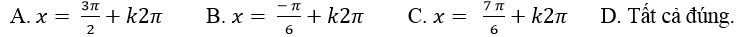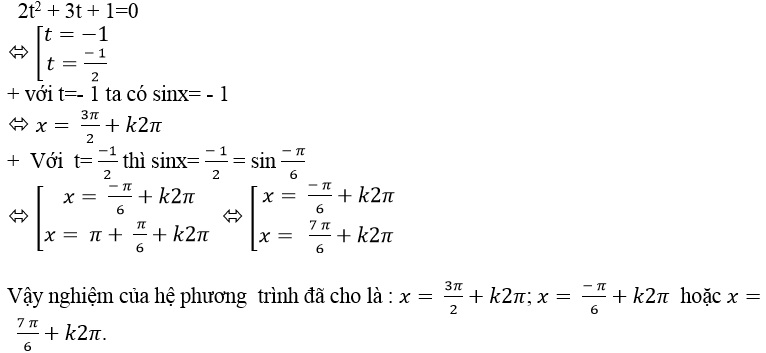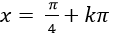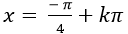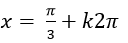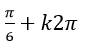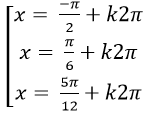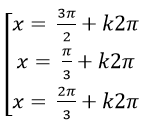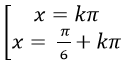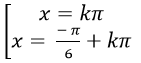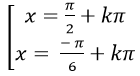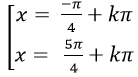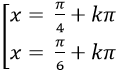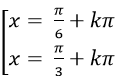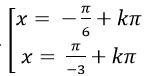Phương trình bậc hai đối với hàm số lượng giác

A. Phương pháp giải

+ Phương trình bậc hai đối với hàm số lượng giác là phương trình có dạng :

a.sin2x + b.sinx + c= 0 (với a ≠ 0)

Tương tự các phương trình a.cos2 x+ b. cosx+ c=0; a. tan2 x + b.tanx + c= 0 và

a.cot2x + b.cotx+ c= 0 ( với a ≠ 0) là các phương trình bậc hai đối với hàm số lượng giác.

+ Xét phương trình: a.sin2 x+ b.sinx+ c= 0 (a ≠ 0) ( các phương trình khác làm tương tự).

• Bước 1: Đặt sinx= t ( - 1 ≤ t ≤ 1). Phương trình đã cho có dạng: at2 + bt+ c= 0 (*)

• Bước 2. Giải phương trình(*) – chú ý chỉ lấy những giá trị của t thỏa mãn -1 ≤ t ≤ 1. Từ đó suy ra: sinx= ....

• Bước 3. Áp dụng cách giải phương trình lượng giác cơ bản

⇒ Nghiệm của phương trình đã cho

B. Ví dụ minh họa

Ví dụ 1. Giải phương trình 2cos² x- 1= 0

A.

B.

C. Cả A và B đúng

D. Đáp án khác

Lời giải

Ta có: 2cos² x – 1= 0 ⇒ cos²x = 1/2

Chọn C.

Ví dụ 2. Giải phương trình : 3cos²x + 3cosx- 6= 0

A.k.π

B.π/2+k.π

C. π/4+k2π

D. π/2+k.2π

Lời giải

Ta có; 3cos²x+ 3cosx- 6= 0 (*).

Đặt cosx= t (-1 ≤ t ≤ 1 ); khi đó phương trình (*) trở thành:

3t² + 3t- 6=0

Với t= 1 ta có; cosx= 1

⇒ x= k.π

Chọn A.

Ví dụ 3. Giải phương trình : tanx.cot(π/2- x) = 1

A.

B.

C.

D.Đáp án khác

Lời giải

Ta có: tanx.cot (90⁰- x) = 1

⇒ tanx. tanx= 1

Chọn C.

Ví dụ 4. Giải phương trình: 4cot² x - 8cotx+ 4= 0

A.arccot⁡2+kπ

B. π/4+kπ

C. π/2+kπ

D. arccot 4+ k.π

Lơì giai

Ta có: 4cot²x- 8cotx + 4= 0 (*)

Đặt t= cotx; khi đó phương trình(*) trở thành:

4t² – 8t + 4= 0

⇒ t= 1 ⇒ cot x= 1

⇒ x= π/4+kπ

Chọn B.

Ví dụ 5. Giải phương trình: tan² x +10tanx+ 35= 0

A. kπ

B. π/4+kπ

C. π/2+kπ

D. phương trình vô nghiệm

Lời giải

Ta có: tan²x+ 10tanx + 35=0 (*)

Đặt t=tanx; khi đó phương trình trên trở thành:

t² + 10t + 35= 0

⇒ Phương trình này vô nghiệm

⇒ Phương trình(*) vô nghiệm

⇒ phương trình đã cho vô nghiệm

Chọn C.

Ví dụ 6. Giải phương trình tan² x+ 3tanx – 4= 0

A.

B.

C.

D.

Lời giải

Ta có: tan² x+ 3tanx – 4= 0 ( *)

Đặt t= tanx; khi đó phương trình (*) trở thành: t² +3t – 4=0

Chọn B.

Ví dụ 7. Giải phương trình: tan² x- √3 tanx=0

A.

B.

C.

D.

Lời giải

Ta có; tan²x- √3 tanx=0 (*)

Đặt tanx= t; khi đó phương trình (*) trở thành:

t²- √3 t=0

Chọn D.

Ví dụ 8. Giải phương trình: sin²x – 2sinx= 0

A . x= k.π

B. x= k2π

C. π/2+kπ

D. Cả A và C đúng

Lời giải

Ta có: sin² x- 2sinx = 0 (*)

Đặt t= sinx (-1 ≤ t ≤ 1); khi đó (*) trở thành:

t² -2t= 0

Với t=0 ta có; sinx= 0

⇒ x= k.π

Chọn A.

Ví dụ 9. Giải phương trình : 2sin²x + 3sinx + 1= 0

Lời giải

Ta có; 2sin2 x+ 3sinx +1= 0 (*)

Đặt t= sinx với - 1 ≤ t ≤ 1; khi đó (*) trở thành:

Chọn D.

C. Bài tập vận dụng

Câu 1:Giải phương trình: √3.sin²x- √6=0

A.

B.

C.

D. Đáp án khác

Câu 2:Biết rằng phương trình : √5cos² x-√5/2=0 có nghiệm là x= aπ/4+kbπ với k∈Z. Tính a+ b?

A. 1

B.2

C. 3

D.4

Câu 3:Giải phương trình : sin² x+ sinx – 6=0?

A.

B.

C.

D.Vô nghiệm

Câu 4: Giải phương trình: 2sin² x + sinx – 1= 0 .

A.

B.

C.

D.

Câu 5:Giải phương trình √2tan² x+ √6 tanx=0

A.

B.

C.

D.

Câu 6:Giải phương trình : 2sin² 2x+ 2√2sin 2x+1= 0 ?

A.

B.

C.

D.

Câu 7:Giải phương trình : √3.tan²x -(√3+1).tanx+1=0

A.

B.

C.

D.

Câu 8:Giải phương trình : cot²x-( √3+ 1/√3)cotx+1=0

A.

B.

C.

D.