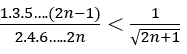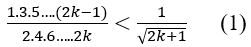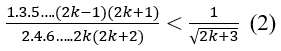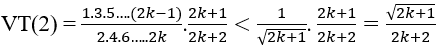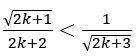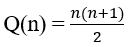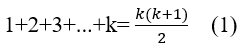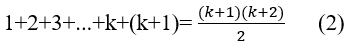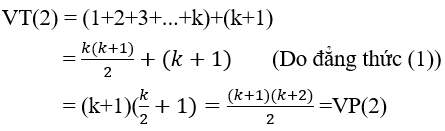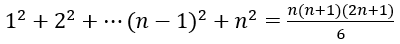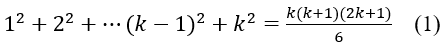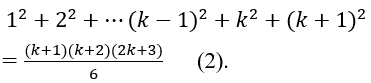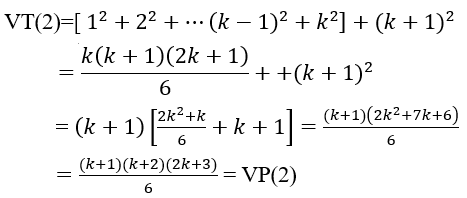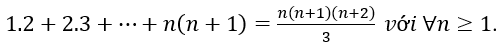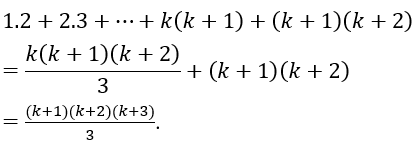Lý thuyết, bài tập Phương pháp quy nạp toán học hay, chi tiết

A. Phương pháp giải & Ví dụ

Giả sử cần chứng minh đẳng thức P(n) = Q(n) (hoặc P(n) > Q(n)) đúng với n ≥ n₀, n₀ ∈ N* ta thực hiện các bước sau:

Bước 1: Tính P(n₀),Q(n₀) rồi chứng minh P(n₀ )= Q(n₀)

Bước 2: Giả sử P(k) = Q(k) ; k ≥ n₀, k ∈ N*, ta cần chứng minh P(k+1) = Q(k+1).

Ví dụ minh họa

Bài 1: Chứng minh rằng vớí ∀n ≥ 1, ta có bất đẳng thức: 

♦ Với n = 1 ta có đẳng thức đã cho trở thành :1/2 < 1/√3 ⇒ 2 > √3 đúng.

⇒ Đẳng thức đã cho đúng với n = 1.

♦ Giả sử đẳng thức đã cho đúng với n = k ≥ 1 , tức là :

Ta phải chứng minh đẳng thức đã cho đúng với n = k+1, tức là :

Thật vậy, ta có :

Ta chứng minh:

⇔ (2k+1)(2k+3) < (2k+2)²

⇒ 3 > 1 (luôn đúng)

Vậy đẳng thức đã cho đúng với mọi số tự nhiên n ≥ 1.

Chú ý: Vậy Phương pháp quy nạp toán học còn được ứng dụng nhiều trong số học và hình học

Bài 2: Chứng mình với mọi số tự nhiên n ≥ 1 ta luôn có: 1+2+3+...+n= (n(n+1))/2

Đặt P(n) = 1+2+3+...+n : tổng n số tự nhiên đầu tiên : 

Ta cần chứng minh P(n) = Q(n) n ≥ 1 ,n ∈ N*.

Bước 1: Với n = 1 ta có P(1) = 1, Q(1) = 1

⇒ P(1) = Q(1) = 1đúng vớí n = 1.

Bước 2: Giả sử P(k0 = Q(k) với k ≥ 1 ,k ∈ N*. tức là:

Ta cần chứng minh P(k+1) = Q(k+1), tức là:

Thật vậy:

Vậy đẳng thức đã cho đúng với mọi n ≥ 1.

Bài 3:Chứng minh với mọi số tự nhiên n ≥ 1 ta luôn có: 1+3+5+⋯+2n-1=n²

♦ Với n = 1 ta có VT =VP = 1

Suy ra đẳng thức đã cho đúng với n = 1.

♦ Giả sử đẳng thức đã cho đúng với n = k với k ≥ 1 ,k ∈ N*. tức là:

1 + 3 + 5 + ... + 2k - 1 = k² (1)

Ta cần chứng minh đẳng thức đã cho đúng với n = k+1, tức là:

1 + 3 + 5 + ... + (2k - 1) + (2k + 1) = (k + 1)² (2)

Thật vậy: VT(2) = 1 + 3 + 5 + ... + (2k - 1) + (2k + 1)

= k² + (2k + 1) = (k + 1)² = VP(2)

Vậy đẳng thức đã cho đúng với mọi n = 1.

B. Bài tập vận dụng

Bài 1: Chứng minh rằng với mọi số tự nhiên n ≥ 1 thì A(n)=7ⁿ+3n-1 luôn chia hết cho 9

Lời giải:

* Với n=1 ⇒ A(1)=7¹+3.1-1=9 ⇒ A(1)chia hết cho 9

* Giả sử A(k)chia hết cho 9 ∀k ≥ 1, ta chứng minh A(k+1)chia hết cho 9

Thật vậy:A(k+1)=7^k+1+3(k+1)1=7.7^k+21k-7-18k+9 ⇒ A(k+1)=7A(k)-9(2k-1)

Vì A(k) chia hết cho 9 và 9(2k-1) chia ết cho 9 nên A(2k+1) chia hết cho 9

Vậy A(n) chia hết cho 9 với mọi số tự nhiên n ≥ 1.

Bài 2: Chứng minh rằng tổng các trong một n – giác lồi (n ≥ 1) bằng (n-2)180º.

Lời giải:

* Với n = 3 ta có tổng ba góc trong tam giác bằng 180º

* Giả sử công thức đúng cho tất cả k-giác, với k < n, ta phải chứng minh mệnh đề cũng đúng cho n-giác. Ta có thể chia n-giác bằng một đường chéo thành ra hai đa giác. Nếu số cạnh của một đa giác là k+1, thì số cạnh của đa giác kia là n – k + 1, hơn nữa cả hai số này đều nhỏ hơn n. Theo giả thiết quy nạp tổng các góc của hai đa giác này lần lượt là. (k-1)180ºvà (n-k-1)180º

Tổng các góc của n-giác bằng tổng các góc của hai đa giác trên, nghĩa là (k-1+n-k-1)180º=(n-2)180º.

Suy ra mệnh đề đúng với mọi n ≥ 3.

Bài 3: Chứng minh rằng với mọi số tự nhiên n ≥ 1 , ta luôn có

Lời giải:

Bước 1: Với n = 1 ta có: VT = 1 ; VP = 1 ⇒ VT=VP

⇒ Đẳng thức đã cho đúng vớí n = 1.

Bước 2: Giả sử đẳng thức đã cho đúng với n = k ≥ 1, tức là

Ta sẽ chứng minh đẳng thức đã cho đúng với n = k+1, tức là cần chứng minh

Thật vậy:

⇒ (1) đúng đẳng thức đã cho đúng với mọi n ≥ 1.

Bài 4: Chứng minh các đẳng thức sau:

Lời giải:

Bài 5: Chứng minh rằng với mọi n ≥ 1 ta có bất đẳng thức:

|sinnx| ≤ k|sinx| ∀x ∈ I

Lời giải:

Làm tương tự câu 1. Với n=1 đẳng thức đã cho đúng

Gợi ý:

* Với n=1 ta có:VT = |sin1.α|=1.|sinα| =VP nên đẳng thức đã cho đúng.

* Giả sử đẳng thức đã cho đúng với n = k+1, tức là :|sinkα| ≤ k|sinα| (1)

Ta phải chứng minh đẳng thức đã cho đúng với n = k+1,tức là :

|sin⁡(k+1)α| ≤ (k+1)|sinα| (2)

Thật vậy:

|sin⁡(k+1)α|=|sinkα.cosα+coskα.sinα| ≤ |sinkα||cosα|+|coskα||sinα| ≤ |sinkα|+|sinα| ≤ k|sinα|+|sinα| ≤ (k+1)|sinα|

Vậy đẳng thức đã cho đúng với n=k+1, nên đẳng thức đã cho cũng đúng với mọi số nguyên dương n.