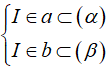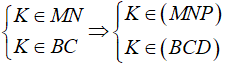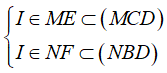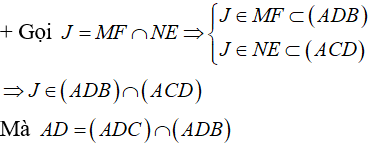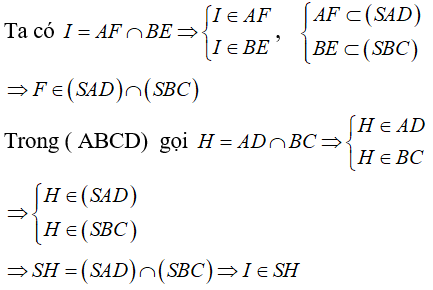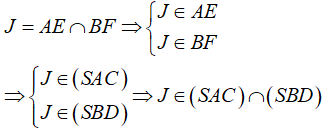Cách tìm quỹ tích giao điểm của hai đường thẳng cực hay

A. Phương pháp giải

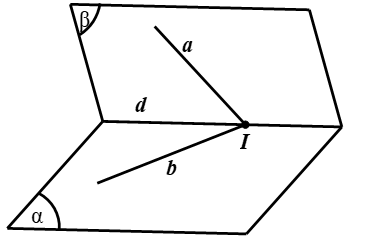
Để tìm tập hợp giao điểm I của hai đường thẳng thay đổi a; b ta chọn hai mặt phẳng cố định

(α) và (β) cắt nhau lần lượt chứa a và b

Khi đó I = a ∩ b ⇒ 

⇒ I ∈ d = (α) ∩ (β)

Vậy điểm I thuộc giao tuyến của hai mặt phẳng (α) và (β)

Để chứng minh đường thẳng d đi qua một điểm cố định ta thực hiện theo các bước sau:

- Chọn một điểm cố định J thuộc hai mặt phẳng (P) và (Q)

- Chứng minh d là giao tuyến của hai mặt phẳng (P) và (Q) , khi đó d đi qua điểm cố định J

B. Ví dụ minh họa

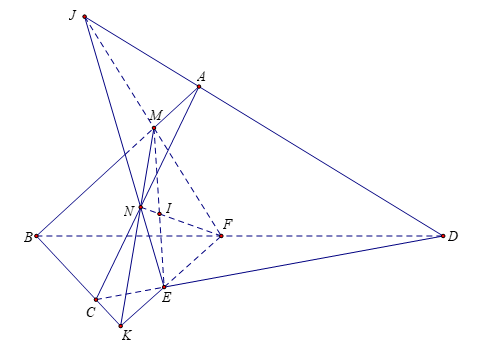
Bài tập 1: Cho tứ diện ABCD. Hai điểm M; N lần lượt nằm trên hai cạnh AB và AC sao cho AM/AB ≠ AN/AC. Một mặt phẳng (P) thay đổi luôn chứa MN, cắt các cạnh CD và BD lần lượt tại E và F .

a) Chứng minh EF luôn đi qua một điểm cố định

b) Tìm tập hợp giao điểm I của ME và NF

c) Tìm tập hợp giao điểm J của MF và NE

Lời giải

a) Trong mp (ABC) gọi K = MN ∩ BC thì K cố định và

Lại có EF = (P) ∩ (BCD) ⇒ K ∈ EF

Vậy EF luôn đi qua điểm K cố định

b) Phần thuận:

Trong (P) gọi I = ME ∩ NF ⇒ 

⇒ I ∈ (MCD) ∩ (NBD)

Gọi O = CM ∩ BN ⇒ OD = (MCD) ∩ (NBD) ⇒ I ∈ OD

Giới hạn:

Khi E chạy đến C thì F chạy đến B và I chạy đến O.

Khi E chạy đến D thì F chạy đến D và I chạy đến D.

Phần đảo:

Gọi I là điểm bất kì trên đoạn OD, trong (MCD) gọi E = MI ∩ CD, trong (NBD) gọi F = NI ∩ BD suy ra (MNEF) là mặt phẳng quay quanh MN cắt các cạnh DB; DC tại các điểm E; F và I = ME ∩ NF

Vậy tập hợp điểm I là đoạn O D.

c)

Khi E chạy đến C thì F chạy đến B và J chạy đến A

Khi E chạy đến D thì F chạy đến D và J chạy đến D

Từ đó ta có tập hợp điểm J là đường thẳng AD trừ các điểm trong của đoạn AD

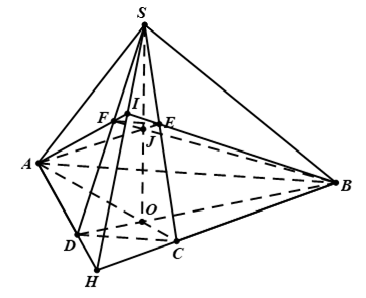
Bài tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn là AB. Một mặt phẳng (P) quay quanh AB cắt các cạnh SC; SD tại các điểm tương ứng E; F

a) Tìm tập hợp giao điểm I của AF và BE

b) Tìm tập hợp giao điểm J của AE và BF

Lời giải

a) Phần thuận:

Giới hạn:

Khi E chạy đến C thì F chạy đến D và I chạy đến H

Khi E chạy đến S thì F chạy đến S và I chạy đến S

Phần đảo:

Lấy điểm I bất kì thuộc đoạn SH , trong (SAH) gọi F = SD ∩ AI, trong (SBH) gọi E là giao điểm của SH và BI. Khi đó (ABEF) là mặt phẳng quay quanh AB cắt các cạnh SC; SD tại E; F và I là giao điểm của AF và BE.

Vậy tập hợp điểm I là đoạn SH

b) Ta có

Nhưng SO = (SAC) ∩ (SBD) nên J ∈ SO

Khi E chạy đến chạy đến C thì F chạy đến D và J chạy đến O

Khi E chạy đến S thì F chạy đến S và J chạy đến S

Lập luận tương tự trên ta có tập hợp điểm J là đoạn SO

C. Bài tập tự luận

Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là trung điểm SB; N là trọng tâm tam giác SCD. Xác định giao điểm của:

a) MN và (ABCD)

b) MN và (SAC)

c) SC và (AMN)

d) SA và (CMN)

Câu 2: Cho tứ diện S.ABCD. Gọi I và J lần lượt là trung điểm của AC và BC. Trên cạnh BD lấy điểm K sao cho BK = 2KD

a) Tìm giao điểm E của CD với mp(IJK). Chứng minh: DE = DC

b) Tìm giao điểm F của AD với mp(IJK). Chứng minh: FA = 2 FD

c) Chứng minh: FK // IJ

d) Gọi M và N là hai điểm bất kì lần lượt nằm trên hai cạnh AB và CD. Tìm giao điểm của MN với mp(IJK)

Câu 3: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi M là trung điểm của SD.

a) Tìm giao điểm I của BM với mp(SAC). Chứng minh: BI = 2IM

b) Tìm giao điểm E của SA với mp(BCM). Chứng minh E là trung điểm của SA

Câu 4: Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB và AB = 2CD. Gọi I, J, K lần lượt là ba điểm trên các cạnh SA; AB; BC

a) Tìm giao điểm của IK và mp (SBD)

b) Tìm giao điểm F của SD và mp (IJK)

Câu 5: Cho tứ diện SABC có D, E lần lượt là trung điểm của AC; BC và G là trọng tâm của tam giác ABC. Mặt phẳng (α) đi qua AC cắt SE; SB lần lượt tại M; N. Một mặt phẳng (β) đi qua BC cắt SD; SA tương ứng tại P và Q.

a) Gọi I = AM ∩ DN, J = BP ∩ EQ. Chứng minh: S; I; J; G thẳng hàng

b) Giả sử K = AN ∩ DM, L = BQ ∩ EP. Chứng minh S; K; L thẳng hàng

Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K là trọng tâm của tam giác SAC và I, J lần lượt là trung điểm của CD và SD

a) Tìm giao điểm H của đường thẳng IK với mặt phẳng (SAB)

b) Xác định thiết diện tạo bởi mặt phẳng (IJK) với hình chóp

Câu 7: Hình chóp S.ABCD có đáy ABCD không là hình thang, điểm P nằm trong tam giác SAB và điểm M thuộc cạnh SD sao cho MD = 2MS

a) Tìm giao tuyến của hai mặt phẳng (SAB) và (PCD)

b) Tìm giao điểm của SC với mặt phẳng (ABM)

c) Gọi N là trung điểm của AD, tìm thiết diện tạo bởi mặt phẳng (MNP) và hình chóp S.ABCD

Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi I,J là trung điểm SA; SB . Lấy điểm M tùy ý trên SD. Tìm giao điểm của:

a) IM và (SBC)     b) JM và (SAC)      c) SC và (IJM)

Câu 9: Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi I, J, K là ba điểm trên SA; AB; BC

a) Tìm giao điểm của IK với (SBD)

b) Tìm các giao điểm của mp (IJK) với SD và SC

Câu 10: Cho hình chóp S.ABCD. Gọi M, N lần lượt là trung điểm của cạnh SA, SD, P là điểm thuộc cạnh SB sao cho: SP = 3PB

a) Tìm giao điểm Q của SC và (MNP)

b) Tìm giao tuyến của (MNP) và (ABCD)

Câu 11: Cho hình chóp S.ABCD. Lấy một điểm M thuộc miền trong tam giác SBC. Lấy một điểm N thuộc miền trong tam giác SCD.

a) Tìm giao điểm của MN với (SAC)

b) Tìm giao điểm của SC với (AMN)

c) Tìm thiết diện của hình chóp S.ABCD với (AMN)

Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N,P lần lượt là trung điểm của SB; SD và OC.

a) Tìm giao tuyến của ( MNP) và (ABCD)

b) Tìm giao điểm của SA và (MNP)

c) Xác định thiết diện của hình chóp với (MNP). Tính tỉ số mà (MNP) chia các cạnh SA, BC và CD