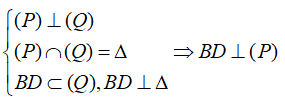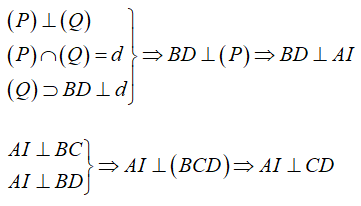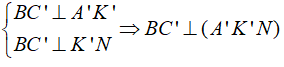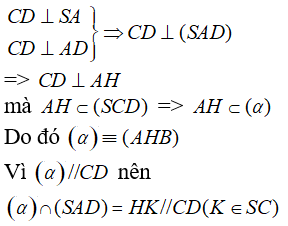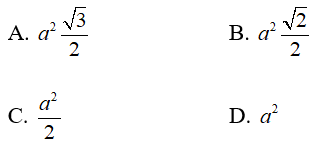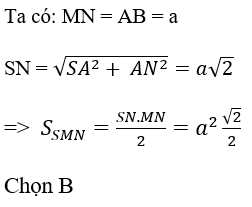Cách xác định thiết diện chứa một đường thẳng và vuông góc với một mặt phẳng

A. Phương pháp giải

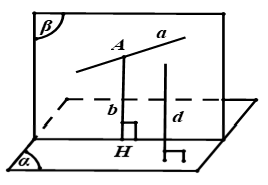
Cho mặt phẳng (α) và đường thẳng a không vuông góc với (α). Xác định mặt phẳng (β) chứa a và vuông góc với (α)

- Để giải bài toán này ta làm theo các bước sau:

+ Chọn một điểm A ∈ a

+ Dựng đường thẳng b đi qua A và vuông góc với (α). Khi đó mp(a; b) chính là mặt phẳng (β).

B. Ví dụ minh họa

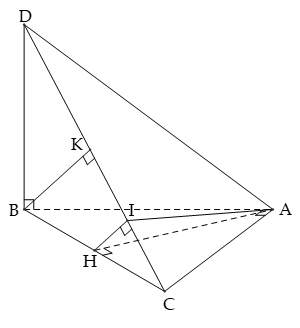
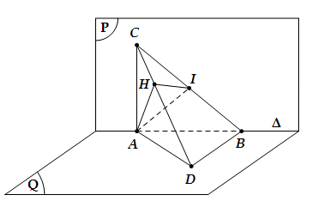
Ví dụ 1: Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến Δ. Lấy A; B cùng thuộc Δ và lấy C trên (P), D trên (Q) sao cho AC ⊥ AB, BD ⊥ AB và AB = AC = BD = a. Diện tích thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) đi qua A và vuông góc với CD là?

Hướng dẫn giải

Chọn C

Ta có:

Gọi H là trung điểm BC, ta có 

Trong mặt phẳng (BCD), kẻ HI ⊥ CD thì ta có CD ⊥ (AHI)

Khi đó mặt phẳng (α) cắt tứ diện ABCD theo thiết diện là tam giác AHI

Mặt khác tam giác ABC vuông cân tại A nên BC = a√2 ⇒ AH = a√2/2

Trong tam giác BCD, kẻ đường cao BK thì BK = a√2/√3 và HI = a/√6

Vậy: thiết diện cần tìm là tam giác AHI vuông tại H và có diện tích S = a²√3/12

Ví dụ 2: Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến Δ. Lấy A; B cùng thuộc Δ và lấy C trên (P), D trên (Q) sao cho AC ⊥ AB, BD ⊥ AB và AB = AC = BD. Thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) đi qua A và vuông góc với CD là hình gì?

A. Tam giác cân.                 B. Hình vuông

C. Tam giác đều.                 D. Tam giác vuông

Hướng dẫn giải

Gọi I là trung điểm của BC

Vì tam giác ABC vuông cân tại A nên AI ⊥ BC

Ta có

Trong (ACD) , dựng đường thẳng đi qua A và vuông góc với CD cắt CD tại H

Thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) là tam giác AHI.

Vì AI ⊥ (BCD) ⇒ AI ⊥ HI nên tam giác AHI là tam giác vuông tại I.

Chọn D

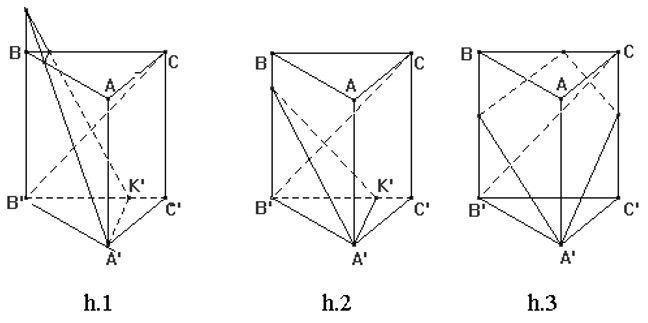
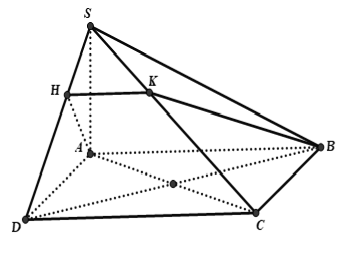
Ví dụ 3: Cho hình lăng trụ đứng AbC.A'B'C' có đáy ABC là tam giác vuông tại A, với AB = c; AC = b , cạnh bên AA’ = h. Mặt phẳng (P) đi qua A’ và vuông góc với B’C. Thiết diện của lăng trụ cắt bởi mặt phẳng (P) có hình:

A. h1 và h2                  B. h2 và h3                 C. h2                 D. h1

Hướng dẫn giải

Gọi (P) là mặt phẳng đi qua A’ và vuông góc với BC.

Từ A’ ta dựng A'K' ⊥ B'C', Vì (ABC) ⊥ (BCC'B') nên A'K' ⊥ B'C' ⇒ A'K' ⊥ (BCC'B') ⇒ A'K' ⊥ BC'   (1)

Mặt khác trong mặt phẳng (BCC'B') dựng K'x ⊥ B'C và cắt BB’ tại 1 điểm N(2) Từ (1) và (2) ta có :

Chọn đáp án A

Ví dụ 4: Cho hình chóp S.ABCD, đáy ABCD là hình vuông, SA ⊥ (ABCD). Gọi (α) là mặt phẳng chứa AB và vuông góc với (SCD), (α) cắt chóp S.ABCD theo thiết diện là hình gì?

A. hình bình hành

B. hình thang vuông

C. hình thang không vuông

D. hình chữ nhật

Hướng dẫn giải

Dựng AH ⊥ CD

Ta có

Từ đó thiết diện là hình thang ABKH

Mặt khác AB ⊥ (SAD) nên AB ⊥ AH

Vậy thiết diện là hình thang vuông tại A và H

Chọn đáp án B

Ví dụ 5: Cho hình chóp S.ABCD với ABCD là hình chữ nhật tâm O có AB = a ; AD = 2a ; SA vuông góc với đáy và SA = a. Gọi (P) là mặt phẳng qua SO và vuông góc với (SAD). Diện tích thiết diện của (P) và hình chóp S.ABCD bằng bao nhiêu?

Hướng dẫn giải

Trong (ABCD) dựng đường thẳng d qua O và d // AB.

Gọi M và N lần lượt là giao điểm của d với BC và AD.

Ta có : AB ⊥ AD và AB ⊥ SA nên AB ⊥ (SAD)

Lại có: MN // AB ⇒ MN ⊥ (SAD).

⇒ ( SMN) ⊥ (SAD)   (1)

Mà SO ⊂ (SMN) nên (P) chính là (SMN).

⇒ Thiết diện của hình chóp cắt bởi mp (P) là tam giác SMN.

Do MN ⊥ (SAD) nên MN ⊥ SN; tam giác SMN vuông tại N.

C. Bài tập vận dụng

Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Cắt hình lập phương bởi mặt phẳng trung trực của AC’. Thiết diện là hình gì?

A. Hình vuông

B. Lục giác đều

C. Ngũ giác đều

D. Tam giác đều