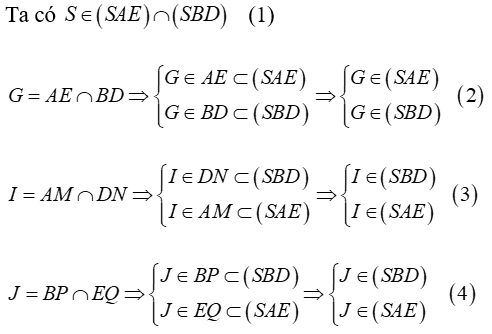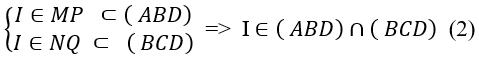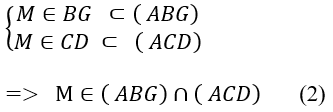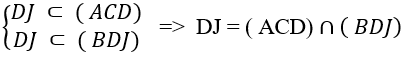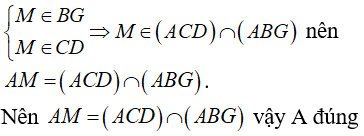Cách chứng minh 3 điểm thẳng hàng, 3 đường thẳng đồng quy

A. Phương pháp giải

- Để chứng minh 3 điểm A; B; C thẳng hàng ta chứng minh 3 điểm đó cùng thuộc 1 đường thẳng hoặc chứng minh 3 điểm đó là điểm chung của hai mặt phẳng (α) và (β) - Khi đó chúng cùng thuộc giao tuyến của 2 mặt phẳng (α) và (β).

- Để chứng minh ba đường thẳng đồng quy ta có thể làm theo những cách sau:

   + Cách 1: chứng minh giao điểm của hai đường này là điểm chung của hai mặt phẳng mà giao tuyến là đường thẳng thứ ba

   + Cách 2: Dựa vào định lí: Ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến khi đó; ba giao tuyến đó đồng quy hoặc đôi một song song

B. Ví dụ minh họa

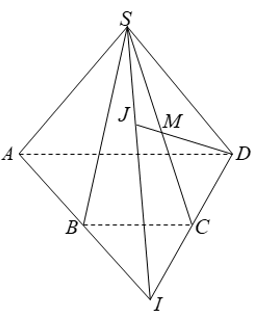
Ví dụ 1: Cho hình chóp S.ABCD có đáy là hình thang ABCD; AD // BC. Gọi I là giao điểm của AB và CD, M là trung điểm SC. DM cắt mặt phẳng (SAB) tại J. Khẳng định nào sau đây sai?

A. S, I; J thẳng hàng

B. DM ⊂ mp (SCI)

C. JM ⊂ mp(SAB)

D. SI = (SAB) ∩ (SCD)

Lời giải

Chọn C

   + Ba điểm S; I và J thẳng hàng vì ba điểm cùng thuộc hai mp

(SAB) và (SCD) nên A đúng

Khi đó: giao tuyến của hai mặt phẳng (SAB) và (SCD) là SI

⇒ D đúng

   + M ∈ SC ⇒ M ∈ (SCI) nên DM ⊂ mp(SCI) vậy B đúng

   + M ∉ (SAB) nên JM ⊄ mp(SAB) vậy C sai

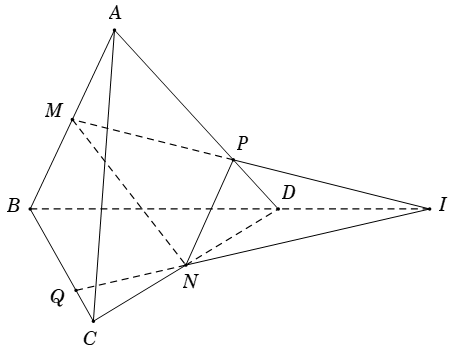
Ví dụ 2: Cho tứ diện SABC có D; E lần lượt là trung điểm của AC; BC và G là trọng tâm của tam giác ABC. Mặt phẳng (α) đi qua AC cắt SE; SB lần lượt tại M, N. Một mặt phẳng (β) đi qua BC cắt SD; SA tương ứng tại P và Q. Gọi I = AM ∩ DN, J = BP ∩ EQ. Khẳng định nào sau đây là đúng?

A. Bốn điểm S, I, J, G thẳng hàng

B. Bốn điểm S, I, J, G không thẳng hàng

C. Ba điểm P, I, J thẳng hàng

D. Bốn điểm I, J, Q thẳng hàng

Lời giải

Từ (1), (2), (3) và (4) ta có S; I; J ; G là điểm chung của hai mặt phẳng (SBD) và (SAE) nên chúng thẳng hàng

Chọn A

Ví dụ 3: Cho hình chóp S.ABCD có đáy ABCD không phải là hình thang. Trên cạnh SC lấy điểm M . Gọi N là giao điểm của SD và mp (AMB). Mệnh đề nào sau đây đúng?

A. Ba đường thẳng AB; CD; MN đôi một song song

B. Ba đường thẳng AB; CD; MN đôi một cắt nhau

C. Ba đường thẳng AB; CD; MN đồng quy

D. Ba đường thẳng AB; CD; MN cùng thuộc một mặt phẳng

Lời giải

- Trong mp (ABCD) gọi I là giao điểm của AD và BC

Trong mp (SBC), gọi K là giao điểm của BM và SI

Trong mp (SAD); gọi N là giao điểm của AK và SD

Khi đó N là giao điểm của đường thẳng SD với mp(AMB)

- Gọi O là giao điểm của AB và CD. Ta có:

   + O ∈ AB mà AB ⊂ (AMB) suy ra O ∈ (AMB)

   + O ∈ CD mà CD ⊂ (SCD) suy ra O ∈ (SCD

⇒ O ∈ (AMB) ∩ (SCD)    (1)

Mà MN = (AMB) ∩ (SCD)    (2)

Từ (1) và (2) , suy ra O ∈ MN.

Vậy ba đường thẳng AB; CD và MN đồng quy.

Chọn C

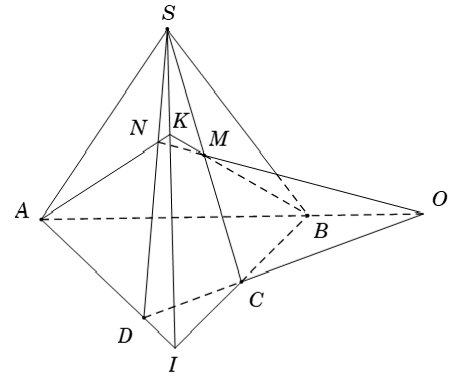
Ví dụ 4: Cho tứ diện ABCD. Gọi M; N lần lượt là trung điểm của AB và CD. Mặt phẳng (P) qua MN và cắt AD; BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Ba điểm nào sau đây thẳng hàng?

A. I; A; C        B. I; B; D         C. I; A; B        D. I; C; D

Lời giải

Ta có: (ABD) ∩ (BCD) = BD    (1)

Lại có 

Từ (1) và (2) suy ra: I ∈ BD hay 3 điểm I; B; D thẳng hàng

Chọn B

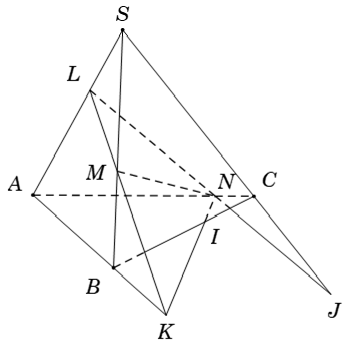
Ví dụ 5: Cho tứ diện SABC. Gọi L; M; N lần lượt là các điểm trên các cạnh SA; SB và AC sao cho LM không song song với AB và LN không song song với SC. Mặt phẳng (LMN) cắt các cạnh AB; BC và SC lần lượt tại K; I; J. Ba điểm nào sau đây thẳng hàng?

A. K; I và J        B. M; I và J        C. N ; I và J        D. M; K và J

Lời giải

Ta có

- M ∈ SB suy ra M isin; (LMN) ∩ (SBC)    (1)

- I ∈ BC ⊂ (SBC) và I ∈ NK ⊂ (LMN)

⇒ I ∈ (LMN) ∩ (SBC)   (2)

- J ∈ SC ⊂ (SBC) và J ∈ LN ⊂ (LMN)

⇒ J ∈ (LMN) ∩ (SBC)     (3)

Vậy M ; I; J thẳng hàng vì cùng thuộc giao tuyến của mp (LMN) và (SBC)

Chọn B

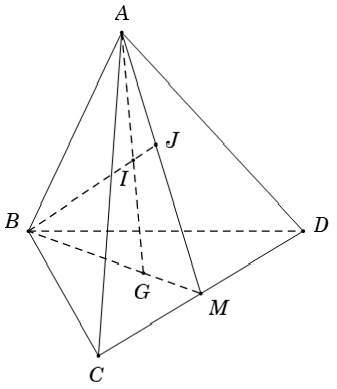
Ví dụ 6: Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD; M là trung điểm CD; I thuộc đoạn AG; BI cắt mp (ACD) tại J. Chọn mệnh đề sai

A. Giao tuyến của (ACD) và (ABG) là AM

B. 3 điểm A; J; M thẳng hàng.

C. J là trung điểm của AM.

D. Giao tuyến của mp(ACD) và (BDJ) là DJ.

Lời giải

Ta xét các phương án:

   + Ta có: A là điểm chung thứ nhất giữa hai mp (ACD) và mp (GAB)    (1)

Do M là giao điểm của BG và CD nên:

Từ (1) và (2) suy ra: giao tuyến của (ABG) và (ACD) là AM ⇒ A đúng

   + Ta có 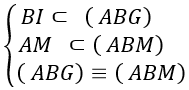 ⇒ AM và BI đồng phẳng

⇒ J = BI ∩ AM nên 3 điểm A; J; M thẳng hàng → B đúng.

   + Ta có 

⇒ D đúng

   + Điểm I di động trên AG nên J có thể không phải là trung điểm của AM.

⇒ C sai

Chọn C

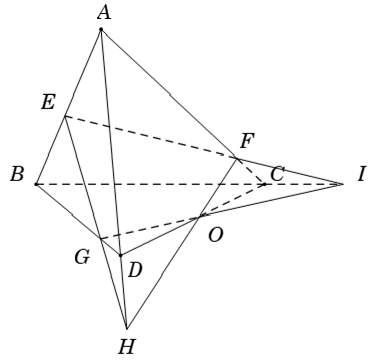
Ví dụ 7: Cho tứ diện ABCD. Gọi E; F; G là các điểm lần lượt thuộc các cạnh AB; AC; BD sao cho EF cắt BC tại I; EG cắt AD tại H. Ba đường thẳng nào sau đây đồng quy?

A. CD; EF; EG          B. CD; IG; HF          C. AB; IG; HF          D, AC; IG; BD

Lời giải

Gọi O là giao điểm của HF và IG . Ta có

- O ∈ HF mà HF ⊂ (ACD) suy ra O ∈ (ACD)

- O ∈ IG mà IG ⊂ (BCD) suy ra O ∈ (BCD)

Do đó O ∈ (ACD) ∩ (BCD)    (1)

Mà (ACD) ∩ (BCD) = CD   (2)

Từ (1) và (2), suy ra O ∈ CD.

Vậy ba đường thẳng CD; IG; HF đồng quy tại O.

Chọn B

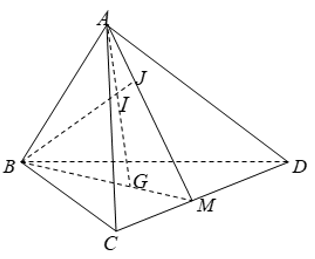
Ví dụ 8: Cho tứ diện ABCD có G là trọng tâm tam giác BCD, M là trung điểm CD, I là điểm trên đoạn thẳng AG, BI cắt mặt phẳng (ACD) tại J. Khẳng định nào sau đây sai?

A. AM = (ACD) ∩ (ABG)

B. A; J; M thẳng hàng

C. J là trung điểm AM

D. DJ = (ACD) ∩ (BDJ)

Lời giải

Chọn C

   + Ba điểm A; J và M cùng thuộc hai mặt phẳng phân biệt (ACD) và (ABG) nên A; J; M thẳng hàng, vậy B đúng

   + Vì I là điểm tùy ý trên AG nên J không phải lúc nào cũng là trung điểm của AM.

C. Bài tập trắc nghiệm

Câu 1: Cho tứ diện SABC. Trên SA; SB và SC lấy các điểm D; E và F sao cho DE cắt AB tại I; EF cắt BC tại J, FD cắt CA tại K. Tìm mệnh đề đúng? Chứng minh ba điểm I; J ; K thẳng hàng.

A. Hai đường thẳng EF và IK chéo nhau

B. 3 điểm I; J; K thẳng hàng

C. Hai đường thẳng JK và DE chéo nhau

D. Tất cả sai

Câu 2: Cho hình chóp tứ giác S.ABCD, gọi O là giao điểm của hai đường chéo AC và BD. Một mặt phẳng (α) cắt các cạnh bên SA; SB;SC và SD tương ứng tại các điểm M, N, P, Q. Khẳng định nào đúng?

A. Các đường thẳng MP, NQ, SO đồng qui

B. Các đường thẳng MP, NQ, SO chéo nhau

C. Các đường thẳng MP, NQ, SO song song

D. Các đường thẳng MP, NQ, SO trùng nhau

Câu 3: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến là đường thẳng a. Trong (P) lấy hai điểm A, B nhưng không thuộc a và S là một điểm không thuộc (P). Các đường thẳng SA; SB cắt (Q) tương ứng tại các điểm C; D. Gọi E là giao điểm của AB và a. Khẳng định nào đúng?

A. AB; CD và a đồng qui

B. AB; CD và a chéo nhau

C. AB; CD và a song song nhau

D. AB; CD và a trùng nhau

Câu 4: Cho hình chóp S.ABCD có đáy là hình thang ABCD (AD // BC) . Gọi I là giao điểm của AB Và CD , M là trung điểm SC; DM cắt mặt phẳng (SAB) tạị J. Khẳng định nào sau đây sai?

A. S; I; J thẳng hàng

B. DM ⊂ mp(SCI)

C. JM ⊂ mp(SAB)

D. SI = (SAB) ∩ (SCD)

Câu 5: Cho hình chóp S.ABCD, AC và BD cắt nhau tại O. Một mặt phẳng cắt các cạnh SA; SB; SC; SD lần lượt tại A’; B’; C’ và D’. Giả sử AD cắt BC tại E; A’D’ cắt B’C’ tại E’. Tìm mệnh đề đúng?

A. 2 đường thẳng SE; EE’ cắt nhau

B. Ba điểm S; E, E’ thẳng hàng.

C. Ba điểm S; E; E’ xác định một mặt phẳng

D. Tất cả sai

D. Bài tập tự luận

Câu 1: Cho hình chóp S.ABCD có AB không song song CD. Gọi M là trung điểm SC và O là giao điểm AC với BD

a) Tìm giao điểm N của SD với (MAB)

b) Chứng minh: SO; AM; BN đồng quy

Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang ,AD là đáy lớn và AD = 2BC. Gọi M, N lần lượt là trung điểm của SB; SC và O là giao điểm của AC và BD.

a) Tìm giao tuyến của (ABN) và (SCD)

b) Tìm giao điểm P của DN và (SAB)

c) Gọi K là giao điểm của AN và DM. Chứng minh 3 điểm S, K, O thẳng hàng. Tính KS/KO

Câu 3: Cho hình chóp S.ABCD, gọi E, F; H lần lượt là các điểm thuộc cạnh SA; SB; SC

a. Tìm giao điểm K = SD ∩ (EFH)

b. AC ∩ BD = O; EH ∩ FK = I. Chứng minh: S; I; O thẳng hàng.

c. AD ∩ BC = M; EK ∩ FH = N. Chứng minh: S, M, N thẳng hàng.

d. AB ∩ CD = P; EF ∩ HK = O. Chứng minh: A, P, Q thẳng hàng.

Câu 4: Cho hình chóp S.ABCD, O là giao điềm của AC và BD. Gọi M là trug điểm của SC và AM cắt SO tại I. Chứng minh 3 đường thẳng SI ; AC; BD đồng quy.

Câu 5: Cho hình chóp S.ABCD, AC và BD cắt nhau tại O. Một mặt phẳng cắt các cạnh SA; SB; SC; SD lần lượt tại A’; B’; C’ và D’. Giả sử AD cắt BC tại E; A’D’ cắt B’C’ tại E’. Chứng minh 3 đường thẳng A’C’; B’D’; SO đồng quy?

Câu 6: Cho tứ diện ABCD. Gọi M; N; P lần lượt là các điểm thuộc cạnh AB; AC; BD MN ∩ BC = I; MP ∩ AD = J; NJ ∩ IP = K. Chứng minh C, D, K thẳng hàng.

Câu 7: Cho tứ giác ABCD có các cạnh đối đôi một không song song, S không thuộc (ABCD). Lấy điểm thuộc cạnh AD, lấy điểm J thuộc cạnh SB.

a) Tìm K = IJ ∩ (SAC)

b) Tìm L = DJ ∩ (SAC)

c) Gọi O = AD ∩ BC, M = OJ ∩ SC. Chứng minh rằng: K, L, M thẳng hàng.

Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M,N lần lượt là trung điểm của SA, SC

a) Tìm giao tuyến của ( BMN) với các mp ( SAB), ( SBC)

b) Tìm I = SO ∩ (BMN), K = SD ∩ (BMN)

c) Tìm E = AD ∩ (BMN), F = CD ∩ (BMN)

d) Chứng minh rằng: B, E, F thẳng hàng.

Câu 9: Cho hình chóp S.ABCD. Gọi I và J là hai điểm trên hai cạnh AD; SB.

a. Tìm giao tuyến của hai mp (SBI) và (SAC). Tìm giao điểm K của IJ và mp(SAC)

b. Tìm giao tuyến của hai mp (SBD) và (SAC). Tìm giao điểm L của DJ và mp(SAC)

c. AD cắt BC tại O; OJ cắt SC tại M. Chứng minh rằng: A; K; L; M thẳng hàng

Câu 10: Cho hình chóp S.ABCD. Gọi M, N là 2 điểm lần lượt nằm trên 2 cạnh BC và SD.

a) Tìm giao điểm I của BN và (SAC)

b) Tìm giao điểm J của MN và (SAC)

c) Chứng minh: I, J, C thẳng hàng

d) Xác định thiết diện của mặt phẳng (BCN) với hình chóp

Câu 11: Cho hình chóp S.ABCD có AB ∩ CD = E, AD ∩ BC = K. Gọi M, N, P lần lượt là trung điểm của SA; SB; SC.

a) Tìm giao tuyến của (SAC) và (SBD)

b) Tìm giao tuyến của (MNP) và (SBD)

c) Tìm giao điểm của Q của SD và (MNP)

d) Gọi H = MN ∩ PQ. Chứng minh: S; H; E thẳng hàng

e) Chứng minh: SK; QM; NP đồng quy

Câu 12: Cho tứ diện ABCD có K là trung điểm của AB . Lấy I, J lần lượt thuộc AC, BD sao cho IA = 2IC; JB = 3JD.

a) Tìm giao điểm E của AD và ( IJK)

b) Tìm giao tuyến d của (IJK) và (BCD)

c) Gọi O là giao điểm của d với CD. Chứng minh I, O, E thẳng hàng

d) Tính các tỉ số OI/OE, OC/OD

Câu 13: Cho tứ diện S.ABC với I trung điểm của SA, J là trung điểm của BC. Gọi M là điểm di động trên IJ và N là điểm di động trên SC.

a) Xác định giao điểm P của MC và (SAB)

b) Tìm giao tuyến của (SMP) và (ABC)

c) Tìm giao điểm E của MN và (ABC)

d) Gọi F = IN ∩ AC. Chứng minh rằng EF luôn đi qua một điểm cố định khi M, N di động