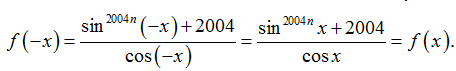Cách xác định tính chẵn, lẻ của hàm số lượng giác cực hay

A. Phương pháp giải

Cho hàm số y= f(x) liên tục và xác định trên khoảng( đoạn ) K. Với mỗi x ∈ K thì-x ∈ K.

+ Nếu f( x)=f(-x) thì hàm số y= f(x) là hàm số chẵn trên tập xác định.

+Nếu f( -x)=-f(x) thì hàm số y= f(x) là hàm số lẻ trên tập xác định .

⇒ Để xác định được tính chẵn; lẻ của một hàm số lượng giác ta làm như sau

+ Tìm tập xác định của hàm số. Với mỗi x ∈ D thì-x ∈ D.

+ Tính f(- x) và – f(x).

+So sánh: f(x) và f( -x);f (-x) và-f(x) ⇒ kết luận .

+ Nếu f(x) ≠ f(-x) và f(-x) ≠ -f(x) thì hàm số y= f(x) là hàm số không chẵn; không lẻ.

B. Ví dụ minh họa

Ví dụ 1: Trong các hàm số sau, hàm số nào là hàm số lẻ?

A.y=x⁴+cos(x-π/3) .

B.y=x²⁰¹⁷+cos(x-π/2) .

C.y=2015+cosx+sin²⁰¹⁸x .

D.y=tan²⁰¹⁷x+sin²⁰¹⁸x .

Lời giải

Chọn B

+ Xét phương án A: y= x⁴+cos⁡( x- π/3)

Hàm số có tập xác định D= R.

Ta có: f(-x)= ( -x)⁴ + cos(-x- π/3)=x⁴+cos⁡( x+ π/3)

Ta có; (f(x) ≠ f( -x )và (-x) ≠ -f(x) nên hàm số đã cho không chẵn; không lẻ.

+ Viết lại đáp án B là y=x²⁰¹⁷+cos(x-π/2) .

Hàm số xác định với mọi x thuộc R,

Ta có: g(-x)= (-x)²⁰¹⁷+sin⁡(-x)=- x²⁰¹⁷-sinx

Suy ra: g(-x) = - g(x) nên hàm số này là hàm số lẻ .

+ xét phương án C: y=h( x) = 2015+ cosx+ sin2018x

Tập xác định D=R.

Ta có: h(-x)= 2015+ cos( -x)+ sin²⁰¹⁸ (-x)

Hay h(-x)=2015+cosx+ [ (-sinx)2018]=2015+ cosx + sin²⁰¹⁸x

⇒ h(x)= h(-x) nên hàm số này là hàm số chẵn.

+ Xét phương án D: y= k(x)= tan²⁰¹⁷x + sin²⁰¹⁸x

Hàm số xác đinh khi x ≠ π/2+kπ

Ta có; k( -x )= tan²⁰¹⁷(-x)+ sin²⁰¹⁸ (-x)= [tan(-x)]²⁰¹⁷+[ sin( -x)]²⁰¹⁸

Hay k( -x ) = -tan²⁰¹⁷x +sin²⁰¹⁸ x

⇒ (k( x) ≠ k(-x)và k(-x) ≠ -k(x) nên hàm số đã cho không chẵn không lẻ.

Ví dụ 2: Cho hàm số 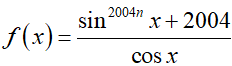, với n ∈ Z. Xét các biểu thức sau:

1, Hàm số đã cho xác định trên .

2, Đồ thị hàm số đã cho có trục đối xứng.

3, Hàm số đã cho là hàm số chẵn.

4, Đồ thị hàm số đã cho có tâm đối xứng.

5, Hàm số đã cho là hàm số lẻ.

6, Hàm số đã cho là hàm số không chẵn không lẻ.

Số phát biểu đúng trong sáu phát biểu trên là

A.1

B.2

C.3

D.4

Lời giải:

Chọn B

Hàm số đã xác định khi cosx≠ 0 < ⇒ x≠ π/2+kπ, k ∈ Z Vậy phát biểu 1 sai.

Ở đây ta cần chú ý: các phát biểu 2; 3; 4; 5; 6 để xác định tính đúng sai ta chỉ cần đi xét tính chẵn lẻ của hàm số đã cho.

Ta có tập xác định của hàm số trên là D=R\{π/2+kπ,k ∈ Z} là tập đối xứng.

Vậy hàm số đã cho là hàm số chẵn.

Suy ra đồ thị hàm số đối xứng qua trục Oy. Vậy chỉ có phát biểu 2 và 3 là phát biểu đúng. Từ đây ta chọn B,

Ví dụ 3: Cho hàm số f(x)=|x|sinx Phát biểu nào sau đây là đúng về hàm số đã cho?

A. Hàm số đã cho có tập xác định D=R\{0} .

B. Đồ thị hàm số đã cho có tâm đối xứng.

C. Đồ thị hàm số đã cho có trục xứng.

D. Hàm số có tập giá trị là [-1;1]

Lời giải:

Chọn B

+ Hàm số đã cho xác định trên tập D=R nên ta loại A

+Tiếp theo để xét tính đối xứng của đồ thị hàm số ta xét tính chẵn lẻ của hàm số đã cho.

Ta có: f(-x)=|-x|sin(-x)=-|x|sinx=-f(x)

Suy ra hàm số đã cho là hàm số lẻ.

Vậy đồ thị hàm số có tâm đối xứng là gốc tọa độ O. Vậy ta chọn đáp án B

Ví dụ 4: Trong các hàm số sau, hàm số nào là hàm số chẵn?

A.y=|sinx| .

B. y= x².sinx

C.y=x/cosx .

D. y= x+ sinx.

Lời giải:

Chọn A

+ Xét phương án A:

Hàm số có tập xác định D= R; ∀ x ∈ D thì -x ∈ D.

Ta có:f(-x)= |sin⁡( -x)|= |- sinx|= |sinx|

⇒ f( x)= f( -x) nên hàm số y= |sinx| là hàm số chẵn

Ví dụ 5. Hàm số nào sau đây là hàm số chẵn?

A. y= - cosx

B. y= -2sinx

C.y=2sin( -x) .

D y= sinx- cosx

Lời giải:

Chọn A

+ xét phương án A: hàm số y= - 2cosx có tập xác định D= R.

Ta có với x ∈ R ⇒ -x ∈ R v à f(-x)=-2cos(-x)=-2cosx.

⇒ f(x)= f( -x)

Vậy hàm số đã cho là hàm số chẵn.

Ví dụ 6: Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. y= sinx    B. y= cosx   C. y= tanx    D. y= cot x

Lời giải:

Chọn B

Nhắc lại kiến thức cơ bản.

+ Hàm số y= sinx là hàm số lẻ.

+ Hàm số y= cosx là hàm số chẵn.

+ Hàm số y= tanx là hàm số lẻ.

+ Hàm số y= cotx là hàm số lẻ.

Vậy B là đáp án đúng.

Ví dụ 7: Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. y= - sinx

B. y= cosx- sinx

C.y= cosx+ sin2x.

D. y= cosx. sinx

Lời giải:

Chọn C

Tất cả các hàm số đều có tập xác định D=R . Do đó ∀x ∈ D ⇒ -x ∈ D .

Bây giờ ta kiểm tra f(-x)=f(x) hoặc f(-x)=-f(x) .

+ xét phương án A:

Với y=f(x)=-sinx .

Ta có f(-x)= -sin(-x)=sinx=-(-sinx)=-f(x).

Suy ra hàm số y= - sinx là hàm số lẻ.

+ Xét phương án B:

Với y=f(x)=cosx-sinx .

Ta có f(-x)=cos(-x)-sin(-x)=cosx+sinx ≠ ±f(x) .

Suy ra hàm số y= cosx- sinx không chẵn không lẻ.

+ Xét phương án C:

Với y=f(x)=cosx+sin²x .

Ta có f(-x)=cos(-x)+sin²(-x)=cosx+sin²x .

Suy ra hàm số y=f(x)=cosx+sin²x là hàm số chẵn.

+ Xét phương án D:

Với y=f(x)= cosx. sinx.

Ta có f(-x)=cos(-x)+sin(-x)=-cosx.sinx=-f(x) .

Suy ra hàm số y= cosx. sinx là hàm số lẻ.

Ví dụ 8: Trong các hàm số sau, hàm số nào là hàm số chẵn?

A.y=2cos(x+π/2)+sin(π-2x) .

B.y=sin(x-π/4)+sin(π+x/4) .

C.y=√2sin(x+π/4)-sinx .

D.y=√(sinx)+√(cosx) .

Lời giải

Chọn C

+ Viết lại đáp án A là y=2cos(x+π/2)+sin(π-2x) = -2sinx+sin2x .

Hàm số xác định với mọi x.

Ta có:f( -x)= - 2sin(-x) + sin( -2x) = 2sinx – sin2x

Và – f(x)= 2sinx – sin2x

⇒ f( -x) = - f(x) nên đây là hàm số lẻ.

+ Viết lại đáp án B là y=sin(x-π/4)+sin(π+x/4)=2sinxcos(π/4)=√(sinx) .

Đây là hàm số lẻ.

+ Viết lại đáp án C là y=√2sin(x+π/4)-sinx=sinx+cosx-sinx=cosx .

Đây là hàm số chẵn.

+ Xét đáp án D :

  Hàm số xác định  .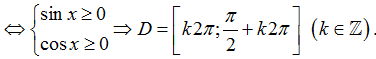

  Chọn x=π/4 ∈ D nhưng -x=-π/4 không thuộc D.

Vậy y=√(sinx)+√(cosx) không chẵn, không lẻ.

Ví dụ 9: Trong các hàm số sau hàm số nào là hàm số lẻ?

A. y= cosx+ sin²x.

B. y= sinx+ cosx.

C. y= - cosx.

D. y= sinx. cos 3x.

Lời giải:

Chọn D

Các hàm số đã cho đều có tập xác định D= R

+ xét phương án A: ta có f(x)= cosx+ sin²x

Và f(-x)= cos( -x)+ sin² (-x)= cosx+ sin²x

⇒ f(x)= f(-x) nên hàm số y= cosx+ sin² x là hàm số chẵn.

+ xét phương án B: y= sinx+ cosx

Ta có: g(x)= sin x+ cos x và g (-x)= sin( - x)+ cos( - x) = - sinx+ cosx

Ta có: (g(x) ≠ g(-x) và -g(x) ≠ g(-x) ⇒ hàm số y= sinx+cosx là không chẵn; không lẻ.

+ Xét phương án C: y= h(x) = - cosx

Ta có: h( -x) = - cos( - x) = - cosx

⇒ h (x)= h(-x) nên hàm số y= - cosx là hàm số chẵn.

+ xét phương án D: y=k(x)= sinx. cos3x

Ta có k(-x) = sin(-x).cos(-3x) = - sin x. cos3x

Và - k(x)= - sinx. cos3x

⇒ k(-x) = - k(x) nên hàm số y= sinx. cos 3x là hàm số lẻ

Ví dụ 11: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?

A.y=cot4x .

B.y=(sinx+1)/cosx .

C.y=tan²x .

D.y=|cotx| .

Lời giải:

Chọn A

Một hàm số có đồ thị đối xứng với nhau qua gốc tọa độ nếu hàm số đó là hàm số lẻ.

+ xét phương án A: y= f( x) = cot 4x

⇒ f( -x) = cot( -4x) = - cot4x và –f(x) = - cot 4x

Suy ra: f( -x) = -f(x) nên hàm số y= f(x) là hàm số lẻ.

⇒ Đồ thị của hàm số y= f(x) đối xứng nhau qua gốc tọa độ.

Ví dụ 12: Trong các hàm số sau, hàm số nào là hàm số lẻ?

A.y=sin(π/2-x) .

B.y=sin²x .

C.y=cotx/cosx .

D.y=tanx/sinx .

Lời giải:

Chọn C

+ xét phương án A:

y= f(x)= sin(π/2-x)=cosx đây là hàm số chẵn

+ Xét phương án B:

y= g(x)= sin2x hàm số này xác định với mọi x.

ta có: g(-x)= sin2(-x)=(- sinx)2 = sin2x

⇒ g(x)= g(-x) nên hàm số đã cho là hàm số chẵn.

+ Xét phương án C. y=h(x)= cotx/cosx

Điều kiện xác định: {(sinx ≠ 0 và cosx ≠ 0 ) ⇒ sin2x ≠ 0 ⇒ x ≠ kπ/2

Với mọi x thuộc tập xác định thì – x cũng thuộc tâp xác định.

Ta có: h(-x)= (cot⁡(-x))/(cos⁡(-x))= (- cotx)/cosx; - h( x) = (- cotx)/cosx

⇒ h(-x) = -h(x) nên hàm số đã cho là hàm số lẻ.

⇒ Chọn C

Ví dụ 13: Hàm số y=cos2x.sin⁡( x- π/4) là

A. Hàm lẻ.

B. Hàm không tuần hoàn.

C. Hàm chẵn.

D. Hàm không chẵn không lẻ.

Lời giải:

Chọn D

Tập xác định D=R. Với ∀x ∈ D thì-x ∈ D.

Ta có : f(-x)=cos⁡(-2x).sin⁡( -x- π/4)=-cos2x.sin⁡( x+ π/4)

Ta thấy f(-x) ≠ f(x) và f(-x)≠ -f(x) .

Vậy hàm số đã cho không chẵn không lẻ.

Ví dụ 14: Xác định tính chẳn lẻ của hàm số: y=1+ 2x² – cos3x

A. Hàm lẻ.

B. Hàm không tuần hoàn.

C. Hàm chẵn.

D. Hàm không chẳn không lẻ.

Lời giải:

Chọn C

Tập xác định D= R là tập đối xứng.

Ta có: f(-x)= 1+ 2( -x)² – cos(-3x) = 1+ 2x²- cos3x

Suy ra: f(x) = f(-x )

Vậy hàm số đã cho là hàm số chẵn.

C. Bài tập vận dụng

Câu 1: Hãy chỉ ra hàm số không có tính chẵn lẻ

A.y=sinx+tanx .

B.y=tanx+1/sinx .

C.y=√2sin(x-π/4) .

D.y=cos⁴- sin⁴ .

Câu 2:Xét hai mệnh đề:

(I)Hàm số y= f( x) = tanx + cosx là hàm số lẻ

(II) Hàm số y= g(x)= tanx+ sinx là hàm số lẻ

Trong hai mệnh đề trên, mệnh đề nào đúng?

A. Chỉ (I) đúng.

B. Chỉ (II) đúng.

C. Cả hai đúng.

D. Cả hai sai.

Câu 3:Hàm số y=10- 2sin²x là:

A. Hàm số chẵn.

B. Hàm số lẻ.

C. Hàm không chẵn không lẻ.

D. Hàm số không tuần hoàn.

Câu 4:Hãy chỉ ra hàm nào là hàm số chẵn:

A.y=sin²⁰¹⁶x.cosx .

B.y=cotx/(tan²+1) .

C.y=sinx.cos6x .

D.y=cosx.sin³x .

Câu 5:Khẳng định nào sau đây là sai?

A.y=|sinx| có đồ thị đối xứng qua gốc tọa độ.

B.y= cosx có đồ thị đối xứng qua trục Oy.

C.y=|tanx| có đồ thị đối xứng qua trục Oy.

D. y=cot x có đồ thị đối xứng qua gốc tọa độ.

Câu 6:Tìm mệnh đề sai:

A. Hàm số y=x.sin³x là hàm chẵn.

B. Hàm số 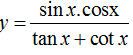 là hàm lẻ.

C. Hàm số 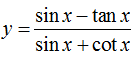 là hàm chẵn.

D. Hàm số y=cos³x +sin³x là hàm số không chẵn không lẻ.

Câu 7:Cho hàm số 

Hàm số trên là hàm số.

A. Hàm lẻ.

B. Hàm không tuần hoàn.

C. Hàm chẵn.

D. Hàm không chẵn không lẻ.

Câu 8:Cho các hàm số sau đây

(I)y=|sinx| .

(II)y=x²sinx .

(III)y=x/cosx .

(IV)y=x+sinx .

Hỏi có bao nhiêu hàm số là hàm lẻ?

A. 1    B. 2    C.3    D. 4

Câu 9:Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?

A.y=sinx.cos2x .

B.y=sin³x.cos(x-π/2) .

C.y=tanx/(tan²+1) .

D.y=cosx.sin³x .

Câu 10:Cho hàm số f( x) = sin2x và g(x)= tan²x. Chọn mệnh đề đúng.

A. f(x) là hàm số chẵn, g(x) là hàm số lẻ.

B. f(x) là hàm số lẻ, g(x) là hàm số chẵn.

C. f(x) là hàm số chẵn, g(x) là hàm số chẵn.

D. f( x) và g(x) đều là hàm số lẻ.

Câu 11:Hàm số nào sau đây là hàm số lẻ?

A.y=-2cosx .

B.y=-2sinx .

C.y=-2sinx²+2 .

D.y=-2cosx+2 .

Câu 12:Hãy chỉ ra hàm số nào là hàm số lẻ:

A.y=√(sinx) .

B.y=sin²x .

C.y=cotx/cosx .

D.y=tanx/sinx .

Câu 13:Hàm số y=tan2x/sin³x có tính chất nào sau đây?

A. Hàm số chẵn.

B. Hàm số lẻ.

C. Hàm không chẵn không lẻ.

D. Tập xác định D=R .

Câu 14:Cho hai hàm số f(x)= 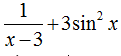 và g(x)=sin√(1-x) . Kết luận nào sau đây đúng về tính chẵn lẻ của hai hàm số này?

A. Hai hàm số f(x); g(x) là hai hàm số lẻ.

B. Hàm số f(x) là hàm số chẵn; hàm số g(x) là hàm số lẻ.

C. Hàm số f(x) là hàm số lẻ; hàm số g(x) là hàm số không chẵn không lẻ.

D. Cả hai hàm số f(x); g(x) đều là hàm số không chẵn không lẻ.

Câu 15:Xét tính chẵn lẻ của hàm số f(x)=sin²⁰⁰⁷ x+cosnx, với n ∈ Z :

A. Hàm số chẵn.

B. Hàm số lẻ.

C. Không chẵn không lẻ.

D. Vừa chẵn vừa lẻ.

Câu 16:Trong các hàm số sau, hàm số nào là hàm số lẻ?

A.y=1-sin²x

B.y=|cotx|.sin²x

C.y=x²tan2x-cotx .

D.y=1+|cotx+tanx| .

Câu 17:Hàm số y= sinx. cos²x + tanx là:

A. Hàm số chẵn.

B. Hàm số lẻ

C. Vừa chẵn vừa lẻ.

D. Không chẵn không lẻ.

Câu 18:Xét tính chẵn lẻ của hàm số y=(1+sin²2x)/(1+cos3x) ta kết luận hàm số đã cho là:

A. Hàm số chẵn.

B. Hàm số lẻ.

C. Vừa chẵn vừa lẻ

D. Không chẵn không lẻ

Câu 19:Xét các mệnh đề sau:

I.Hàm số là hàm số lẻ.

II.Hàm số là hàm số chẵn.

III.Hàm số là hàm số lẻ.

Trong các mệnh đề trên, mệnh đề nào đúng?

A. Chỉ (I).

B. Chỉ (II).

C.(II) và (III).

D. Cả 3 Câu.