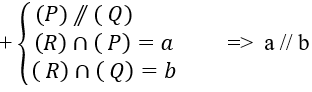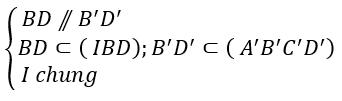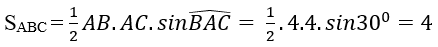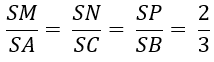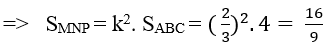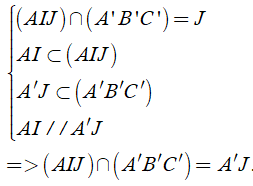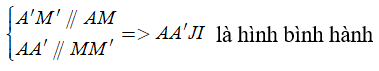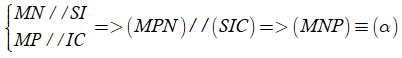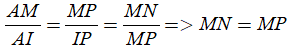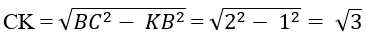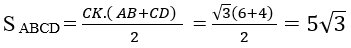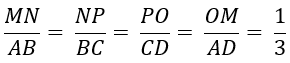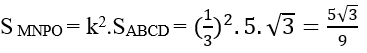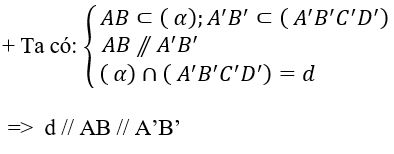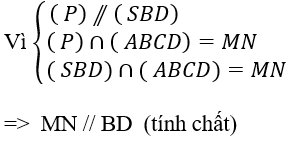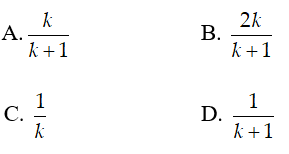Tìm giao tuyến của 2 mặt phẳng. Thiết diện qua 1 điểm song song với mặt phẳng

A. Phương pháp giải

Xác định lần lượt các giao tuyến của (P) với các mặt của hình chóp (lăng trụ) theo các bước sau

- Từ điểm chung có sẵn , xác định giao tuyến đầu tiên của (P) với một mặt của hình chóp (Có thể là mặt trung gian)

- Cho giao tuyến này cắt các cạnh của mặt đó của hình chóp ta sẽ được các điểm chung mới của (P) với các mặt khác. Từ đó xác định được các giao tuyến mới với các mặt này

- Tiếp tục như thế cho tới khi các giao tuyến khép kín ta được thiết diện .

Sử dụng định lí:

   + Hai mặt phẳng chứa hai đường thẳng song song thì giao tuyến của chúng song song với 2 đường thẳng đó

B. Ví dụ minh họa

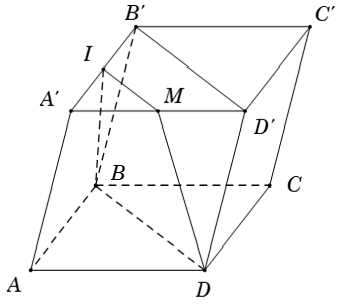
Ví dụ 1: Cho hình hộp ABCD.A’B’C’D’. Gọi I là trung điểm của A’B’. Mặt phẳng (IBD) cắt hình hộp theo thiết diện là hình gì?

A. Tam giác

B. Hình thang

C. Hình bình hành.

D. Hình chữ nhật

Lời giải

   + Ta tìm giao tuyến của 2 mp(IBD) và (A’B’C’D’) :

⇒ Giao tuyến của (IBD) với (A’B’C’D’) là đường thẳng d đi qua I và song song với BD

   + Trong mặt phẳng (A’B’C’D’) , gọi M là giao điểm của d và A’D’

⇒ IM // BD // B’D’

Khi đó thiết diện là tứ giác IMDB và tứ giác này là hình thang

Chọn B

Ví dụ 2: Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn: AB = AC = 4; ∠BAC = 30°. Mặt phẳng (P) song song với (ABC) cắt đoạn SA tại M sao cho SM = 2MA. Diện tích thiết diện của (P) và hình chóp S.ABC bằng bao nhiêu?

A. 16/9       B. 14/9      C. 25/9       D. 1

Lời giải

   + Diện tích tam giác ABC là:

   + Gọi N; P lần lượt là giao điểm của mặt phẳng (P) và các cạnh SC; SB

   + Vì (P) // (ABC) nên theoo định lí Talet, ta có:

Khi đó (P) cắt hình chóp S.ABC theo thiết diện là tam giác MNP đồng dạng với tam giác ABC theo tỉ số k = 2/3.

Chọn A

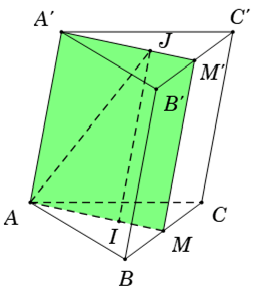
Ví dụ 3: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi I; J lần lượt là trọng tâm của các tam giác ABC và A’B’C’. Thiết diện tạo bởi mặt phẳng (AIJ) với hình lăng trụ đã cho là:

A. Tam giác cân    B. Tam giác vuông    C. Hình thang    D. Hình bình hành.

Lời giải

Kéo dài AI cắt BC tại M, suy ra M là trung điểm BC

Ta có

Trong mặt phẳng (A’B’C’), gọi M' = A'J ∩ B'C'

Khi đó thiết diện là tứ giác AA’JI, tứ giác này có

Chọn D

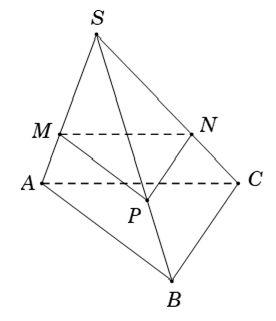
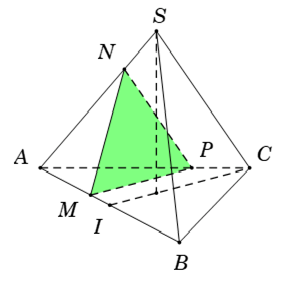
Ví dụ 4: Cho tứ diện đều S.ABC. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng (α) song song với (SIC). Thiết diện tạo bởi (α) với tứ diện S.ABC là:

A. Tam giác cân tại M

B. Tam giác đều

C. Hình bình hành

D. Hình thoi

Lời giải

Gọi N; P lần lượt nằm trên các cạnh SA; AC sao cho

Vậy thiết diện là tam giác MNP.

Tứ diện S.ABC đều nên tam giác SIC cân tại I

Ngoài ra ta có 

Suy ra tam giác MNP cân tại M

Chọn A

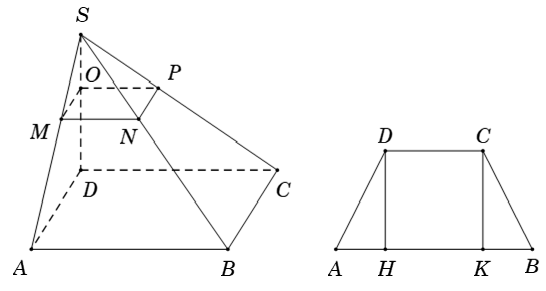
Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với cạnh bên BC = 2 hai đáy AB = 6 và CD = 4. Mặt phẳng (P) song song với (ABCD) và cắt cạnh SA tại M sao cho SA = 3 SM. Diện tích thiết diện của (P) và hình chóp S.ABCD bằng bao nhiêu?

Lời giải

Gọi H; K lần lượt là hình chiếu vuông góc của D; C trên AB

   + Tứ giác DCKH là hình chữ nhật (hình bình hành có 1 góc vuông) nên CD = HK = 4

   + Ta có; AH = KB và AH + HK + KB = AB

⇒ 2.AH + 4 = 6 nên AH = KB = 1

   + Áp dụng định lí Pytago vào tam giác vuông CKB có:

Suy ra diện tích hình thang ABCD là:

   + Gọi N; P; O lần lượt là giao điểm của (P) và các cạnh SB; SC; SD

Vì (P) // (ABCD) nên theo định lí Talet, ta có:

Khi đó (P) cắt hình chóp theo thiết diện là MNPO có diện tích:

Chọn A

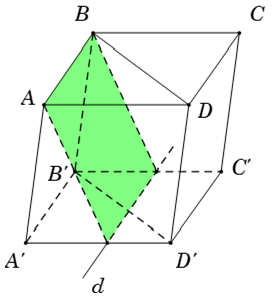
Ví dụ 6: Cho hình hộp ABCD.A’B’C’D’. Gọi (α) là mặt phẳng đi qua một cạnh của hình hộp và cắt hình hộp theo thiết diện là một tứ giác (T). Khẳng định nào sau đây không sai?

A. (T) là hình chữ nhật

B. (T) là hình bình hành

C. (T) là hình thoi

D. (T) là hình vuông

Lời giải

   + Giả sử mặt phẳng (α) đi qua cạnh AB và cắt hình hộp theo tứ giác (T)

   + Gọi d là đường thẳng giao tuyến của (α) và mặt phẳng (A’B’C’D’)

   + Gọi d cắt A’D’ và B’C’ tại M và N khi đó MN = AB và MN // AB

⇒ Thiết diện cần tìm là hình bình hành ABNM.

Chọn B

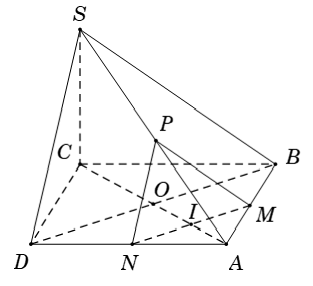
Ví dụ 7: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Tam giác SBD đều. Một mặt phẳng (P) song song với (SBD) và qua điểm I thuộc cạnh AC (không trùng với A hoặc C). Thiết diện của (P) và hình chóp là hình gì?

A. Hình hình hành

B. Tam giác cân

C. Tam giác vuông

D. Tam giác đều

Lời giải

Gọi MN là đoạn thẳng giao tuyến của mặt phẳng (P) và mặt đáy (ABCD).

   + Lập luận tương tự, ta có

(P) cắt mặt (SAD) theo đoạn giao tuyến NP với NP // SD

(P) cắt mp (SAB) theo đoạn giao tuyến MP với MP // SB

Vậy tam giác PMN đồng dạng với tam giác SBD nên thiết diện của (P) và hình chóp S.ABCD là tam giác đều MNP.

Chọn D

Ví dụ 8: Nếu thiết diện của một lăng trụ tam giác và một mặt phẳng là một đa giác thì đa giác đó có nhiều nhất mấy cạnh?

A. 3 cạnh     B. 4 cạnh     C. 5 cạnh     D. 6 cạnh.

Lời giải

Chọn C

Đa giác thiết diện của một lăng trụ tam giác và một mặt phẳng có nhiều nhất 5 cạnh với các cạnh thuộc các mặt của hình lăng trụ tam giác.

C. Bài tập trắc nghiệm

Câu 1: Cho tứ diện ABCD và M; N là các điểm thay trên các cạnh AB; CD sao cho AM/MB = CN/ND = k.

a) Chứng minh MN luôn luôn song song với một mặt phẳng cố định.

b) Tính theo k tỉ số diện tích tam giác MNP và diện tích thiết diện.

Câu 2: Cho hình hộp ABCD.A’B’C’D’ có tất cả các mặt đều là hình vuông cạnh a. Các điểm M; N lần lượt trên AD’; BD sao cho AM = DN = x (0 < x < a√2)

a) Chứng minh khi x biến thiên, đường thẳng MN luôn song song với một mặt phẳng cố định

b) Chứng minh khi x = (a.√2)/3 thì MN // A’C

Câu 3: Nếu thiết diện của một hình hộp và một mặt phẳng là một đa giác thì đa giác đó có nhiều nhất mấy cạnh ?

A. 4 cạnh

B 5 cạnh

C. 6 cạnh

D. 7 cạnh

Câu 4: Cho hình hộp ABCD.A’B’C’D’. Gọi M là trung điểm của AB. Mặt phẳng (MA’C’) cắt hình hộp ABCD.A’B’C’D’ theo thiết diện là hình gì?

A. Hình tam giác

B. Hình ngũ giác

C. Hình lục giác

D. Hình thang

Câu 5: Cho tứ diện đều S.ABC cạnh bằng a. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng (α) song song với (SIC). Tính chu vi của thiết diện tạo bởi (α) với tứ diện S.ABC, biết AM = x

A. x(1 + √3)      B. 2x(1 + √3)    C. 3x(1 + √3)    D. Không tính được.

Câu 6: Cho hình vuông ABCD và tam giác đều SAB nằm trong hai mặt phẳng khác nhau. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng (α) song song với (SBC). Thiết diện tạo bởi (α) và hình chóp S.ABCD là hình gì?

A. Hình tam giác

B. Hình bình hành

C. Hình thang

D. Hình vuông

Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có tâm O; AB = 8, SA = SB = 6. Gọi (P) là mặt phẳng qua O và song song với (SAB). Tính diện tích thiết diện của (P) và hình chóp S.ABCD là:

A. 5√5       B. 6√5       C. 12       D. 10

Câu 8: Cho hình vuông ABCD và tam giác đều SAB nằm trong hai mặt phẳng khác nhau. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng (α) song song với (SBC). Gọi N; P; Q lần lượt là giao của mặt phẳng (α) với các đường thẳng CD; SD; SA. Tập hợp các giao điểm I của hai đường thẳng MQ và NP là:

A. Đường thẳng song song với AB

B. Nửa đường thẳng

C. Đoạn thẳng song song với AB

D. Tập hợp rỗng

Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M; N lần lượt là trung điểm của AB; CD. Xác định thiết diện của hình chóp cắt bởi (α) đi qua MN và song song với mặt phẳng (SAD). Thiết diện là hình gì?

A. Tam giác

B. Hình thang

C. Hình bình hành

D. Tứ giác

Câu 10: Cho hình chóp cụt tam giác ABC.A’B’C’ có 2 đáy là 2 tam giác vuông tại A và A’ và có AB/A'B' = 1/2. Khi đó tỉ số diện tích : S_ABC/S_A'B'C' bằng:

A. 1/2       B. 1/4      C. 2     D. 4

Câu 11: Cho hình hộp ABCD.A’B’C’D’. Gọi I là trung điểm AB. Mp (IB’D’) cắt hình hộp theo thiết diện là hình gì?

A. Tam giác

B. Hình thang

C. Hình bình hành

D. Hình chữ nhật

Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, gọi M là trung điểm của OC. Mặt phẳng (α) qua M song song với SA và BD. Thiết diện của hình chóp với mặt phẳng (α) là:

A. Hình tam giác

B. Hình bình hành

C. Hình chữ nhật

D. Hình thang