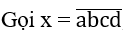Cách giải bài toán đếm số phương án cực hay

Lý thuyết và Phương pháp giải

A. Qui tắc cộng:

a) Định nghĩa: Một công việc nào đó có thể được thực hiện theo một trong hai phương án A hoặc B. Nếu phương án A có m cách thực hiện, phương án B có n cách thực hiện và không trùng với bất kì cách nào trong phương án A thì công việc đó có m + n cách thực hiện.

b) Công thức quy tắc cộng:

Nếu các tập A₁, A₂,..., A_n đôi một rời nhau. Khi đó:

        |A₁ ∪ A₂ ∪ … ∪ A_n | = |A₁ |+|A₂ |+⋯+|A_n |

c) Phương pháp đếm bài toán tổ hợp dựa vào quy tắc cộng:

Để đếm số cách thực hiện một công việc H nào đó theo quy tắc cộng ta cần phân tích xem công việc H đó có bao nhiêu phương án thực hiện? Mỗi phương án có bao nhiêu cách chọn?

B. Qui tắc nhân:

a) Định nghĩa: Một công việc nào đó có thể bao gồm hai công đoạn A và B. Nếu công đoạn A có m cách thực hiện và ứng với mỗi cách đó có n cách thực hiện công đoạn B thì công việc đó có m.n cách thực hiện.

b) Công thức quy tắc nhân:

Nếu các tập A₁, A₂,..., A_n đôi một rời nhau. Khi đó:

        |A₁ ∩ A₂ ∩ … ∩ A_n | = |A₁ |.|A₂ |…|A_n |

c) Phương pháp đếm bài toán tổ hợp dựa vào quy tắc nhân:

Để đếm số cách thực hiện công việc H theo quy tắc nhân, ta cần phân tích công việc H được chia làm các giai đoạn H₁, H₂,..., H_n và đếm số cách thực hiện mỗi giai đoạn H_i (i = 1, 2,..., n).

Chú ý: Ta thường gặp bài toán đếm số phương án thực hiện hành động H thỏa mãn tính chất T. Để giải bài toán này ta thường giải theo hai cách sau

Cách 1: Đếm trực tiếp

    ♦ Nhận xét đề bài để phân chia các trường hợp xảy ra đối với bài toán cần đếm.

    ♦ Đếm số phương án thực hiện trong mỗi trường hợp đó

    ♦ Kết quả của bài toán là tổng số phương án đếm trong cách trường hợp trên

Cách 2: Đếm gián tiếp (đếm phần bù)

Trong trường hợp hành động H chia nhiều trường hợp thì ta đi đếm phần bù của bài toán như sau:

    ♦ Đếm số phương án thực hiện hành động (không cần quan tâm đến có thỏa tính chất T hay không) ta được a phương án.

    ♦ Đếm số phương án thực hiện hành động H không thỏa tính chất T ta được b phương án.

Khi đó số phương án thỏa yêu cầu bài toán là: a - b.

Đếm số phương án liên quan đến số tự nhiên

A. Phương pháp giải & Ví dụ

Ta sử dụng phương pháp chung và một số lưu ý sau:

Khi lập một số tự nhiên 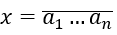 ta cần lưu ý:

* a_i ∈ {0,1,2,…,9} và a₁ ≠ 0.

* x là số chẵn ⇔ a_n là số chẵn.

* x là số lẻ ⇔ a_n là số lẻ.

* x chia hết cho 3 ⇔ a₁+a₂+⋯+a_n chia hết cho 3.

* x chia hết cho 4 ⇔  chia hết cho 4.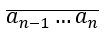

* x chia hết cho 5 ⇔ a_n=0 hoặc a_n=5.

* x chia hết cho 6 ⇔ x là số chẵn và chia hết cho 3.

* x chia hết cho 8 ⇔  chia hết cho 8.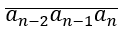

* x chia hết cho 9 ⇔ a₁+a₂+⋯+a_n chia hết cho 9.

* x chia hết cho 11⇔ tổng các chữ số ở hàng lẻ trừ đi tổng các chữ số ở hàng chẵn là một số chia hết cho 11.

* x chia hết cho 25 ⇔ hai chữ số tận cùng là 00, 25, 50, 75.

Ví dụ minh họa

Bài 1: Cho tập A = {0,1,2,3,4,5,6}.Từ tập A ta có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau.

Đáp án và hướng dẫn giải

a,b,c,d ∈ {0,1,2,3,4,5,6}, a ≠ 0.

Vì a ≠ 0 nên a có 6 cách chọn a ∈ {1,2,3,4,5,6}.

Với mỗi cách chọn a ta có 6 cách chọn b ∈ {0,1,2,3,4,5,6}\{a}.

Với mỗi cách chọn a,b ta có 5 cách chọn c ∈ {0,1,2,3,4,5,6}\{a,b}.

Với mỗi cách chọn a,b, c ta có 4 cách chọn d ∈ {0,1,2,3,4,5,6}\{a,b,c}.

Vậy có 6.6.5.4 = 720 số cần lập.

Bài 2: Có bao nhiêu chữ số chẵn gồm bốn chữ số đôi một khác nhau được lập từ các số 0,1,2,4,5,6,8.

Đáp án và hướng dẫn giải

a,b,c,d ∈ {0,1,2,4,5,6,8}, a ≠ 0.

Vì x là số chẵn nên d ∈ {0,2,4,6,8}.

TH1: d = 0 ⇒ có 1 cách chọn d.

Vì a ≠ 0 nên ta có 6 cách chọn a ∈ {1,2,4,5,6,8}.

Với mỗi cách chọn a, d ta có 5 cách chọn b ∈ {1,2,4,5,6,8}\{a}.

Với mỗi cách chọn a, b, d ta có 4 cách chọn c ∈ {1,2,4,5,6,8}\{a,b}.

Suy ra trong trường hợp này có 1.6.5.4 = 120 số.

TH2: d ≠ 0, d chẵn nên d ∈ {2,4,6,8}. Vậy có 4 cách chọn d

Với mỗi cách chọn d, do a ≠ 0 nên ta có 5 cách chọn a ∈ {1,2,4,5,6,8}\{d}.

Với mỗi cách chọn a,d ta có 5 cách chọn b ∈ {0,1,2,4,5,6,8}\{a,d}.

Với mỗi cách chọn a, b, d ta có 4 cách chọn c ∈ {0,1,2,4,5,6,8}\{a,d,b}.

Suy ra trong trường hợp này có 4.5.5.4= 400 số.

Vậy có tất cả 120 + 400 = 520 số cần lập.

Đếm số phương án liên quan đến kiến thức thực tế

A. Phương pháp giải & Ví dụ

Ta sử dụng phương pháp chung để làm các bài toán dạng này.

Ví dụ minh họa

Bài 1: Một túi có 20 viên bi khác nhau trong đó có 7 bi đỏ, 8 bi xanh và 5 bi vàng. Hỏi có bao nhiêu cách lấy 3 viên bi khác màu?

Đáp án và hướng dẫn giải

Việc chọn 3 viên bi khác màu phải tiến hành 3 hành động liên tiếp: chọn 1 bi đỏ trong 7 bi đỏ nên có 7 cách chọn, tương tự có 8 cách chọn 1 bi xanh và 5 cách chọn 1 bi vàng. Theo quy tắc nhân ta có: 7.8.5 = 280 cách.

Bài 2: Từ thành phố A đến thành phố B có 6 con đường, từ thành phố B đến thành phố C có 7 con đường. Có bao nhiêu cách đi từ thành phố A đến thành phố C, biết phải đi qua thành phố B.

Đáp án và hướng dẫn giải

Để đi từ thành phố A đến thành phố B ta có 6 con đường để đi. Với mỗi cách đi từ thành phố A đến thành phố B ta có 7 cách đi từ thành phố B đến thành phố C. Vậy có 6.7 = 42 cách đi từ thành phố A đến C.

Bài 3: Một lớp có 23 học sinh nữ và 17 học sinh nam.

a) Hỏi có bao nhiêu cách chọn một học sinh tham gia cuộc thi tìm hiểu môi trường?

b) Hỏi có bao nhiêu cách chọn hai học sinh tham gia hội trại với điều kiện có cả nam và nữ?

Đáp án và hướng dẫn giải

a) Theo quy tắc cộng có: 23 +17 = 40 cách chọn một học sinh tham gia cuộc thi môi trường.

b) Việc chọn hai học sinh (nam và nữ) phải tiến hành hai hành động liên tiếp

Hành động 1: chọn 1 học sinh nữ trong số 23 học sinh nữ nên có 23 cách chọn

Hành động 2: chọn 1 học sinh nam có 17 cách chọn

Theo quy tắc nhân, có 23.17=391 cách chọn hai học sinh tham gia hội trại có cả nam và nữ.

Cách giải Bài toán xếp vị trí, phân công công việc

A. Phương pháp giải & Ví dụ

Dựa vào hai quy tắc cộng, quy tắc nhân và các khái niệm hoán vị, chỉnh hợp, tổ hợp, đếm gián tiếp, đếm phần bù.

Một số dấu hiệu giúp chúng ta nhận biết được hoán vị, chỉnh hợp hay tổ hợp.

1) Hoán vị: Các dấu hiệu đặc trưng để giúp ta nhận dạng một hoán vị của n phần tử là:

        ♦ Tất cả n phần tử đều phải có mặt

        ♦ Mỗi phần tử xuất hiện một lần.

        ♦ Có thứ tự giữa các phần tử.

2) Chỉnh hợp: Ta sẽ sử dụng khái niệm chỉnh hợp khi

        ♦ Cần chọn k phần tử từ n phần tử, mỗi phần tử xuất hiện một lần

        ♦ k phần tử đã cho được sắp xếp thứ tự.

3) Tổ hợp: Ta sử dụng khái niệm tổ hợp khi

        ♦ Cần chọn k phần tử từ n phần tử, mỗi phần tử xuất hiện một lần

        ♦ Không quan tâm đến thứ tự k phần tử đã chọn.

Ví dụ minh họa

Bài 1: Một nhóm có 5 nam và 3 nữ. Chọn ra 3 người sao cho trong đó có ít nhất 1 nữ. Hỏi có bao nhiêu cách.

Bài 2: Đội tuyển HSG của một trường gồm 18 em, trong đó có 7 HS khối 12, 6 HS khối 11 và 5 HS khối10. Hỏi có bao nhiêu cách cử 8 cách cử 8 HS đi dự đại hội sao cho mỗi khối có ít nhất 1 HS được chọn