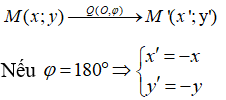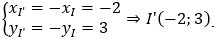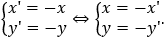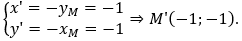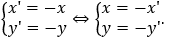Dạng bài tập về phép quay 180 độ cực hay

A. Phương pháp giải

B. Ví dụ minh họa

Ví dụ 1: Trong mặt phẳng Oxy, cho đường tròn (C): (x - 2)² + (y + 3)² = 9. Tìm ảnh của đường tròn (C) qua phép quay tâm O, góc quay 180°.

Hướng dẫn giải:

Cách 1:

+) Đường tròn (C) có tâm I(2;-3) và bán kính R = 3.

+ Gọi C'(I',R') là ảnh của (C) qua phép quay Q_(0,180°).

Khi đó ta có: R' = R = 3 và Q_(0,180°)(I) = I', suy ra: 

+) Vậy (C') có PT là: (x + 2)² + (y - 3)² = 9.

Cách 2:

+ Gọi (C') là ảnh của (C) qua phép quay Q_(0,180°).

+) Với mọi điểm M(x;y) ∈ (C), M'(x';y') ∈ (C') sao cho Q_(0,180°)(M) = M'.

+) Khi đó ta có: 

+) Do M(x;y) ∈ (C) nên ta có: (x - 2)² + (y + 3)² = 9 ⇔ (-x' - 2)² + (-y' + 3)² = 9 ⇔ (x' + 2)² + (y' - 3)² = 9

+) Do M'(x';y') ∈ (C') nên (C') có PT là (x + 2)² + (y - 3)² = 9.

Chú ý: Ưu tiên giải cách 1.

Cách 3:

Chú ý công thức nhanh: Trong mpOxy, cho (C): (x - A)² + (y - B)² = R².

Nếu Q_((O,α)) ((C)) = (C') và α = π + k2π thì (C'): (x + A)² + (y + B)² = R².

+) Do (C): (x - 2)² + (y + 3)² = 9 và Q_(0,180°)((C)) = (C') nên (C') có PT là: (x + 2)² + (y - 3)² = 9.

Ví dụ 2: Trong mặt phẳng Oxy, cho các điểm A(1;2) và B(-3;4). Tìm ảnh của điểm A và B qua phép Quay tâm O góc quay 180°

Hướng dẫn giải:

● Gọi A’ là ảnh của điểm A qua phép quay tâm O góc quay 180°. Khi đó: A’( -1;-2)

● Gọi B’ là ảnh của điểm B qua phép quay tâm O góc quay 180°. Khi đó: B’( 3;-4)

Ví dụ 3: Trong mặt phẳng Oxy, cho đường thắng d: 2x - 5y + 3 = 0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép quay tâm O, góc quay 180°.

Hướng dẫn giải:

Cách 1:

+) Do Q_(0,180°)(d) = d' nên d'//d. Do đó d' có PT dạng: 2x - 5y + m = 0 (m ≠ 3).

+) Chọn M(1;1) ∈ d, gọi M'(x';y') ∈ d' là ảnh của điểm M qua phép quay Q_(0,180°).

Suy ra: 

+) Do M'(-1;-1) ∈ d' nên 2.(-1) - 5.(-1) + m = 0 ⇔ m = -3.

+) Vậy d' có PT là 2x - 5y - 3 = 0.

Cách 2:

+) Với mọi điểm M(x;y) ∈ d, M'(x';y') ∈ d' sao cho A.

+) Khi đó ta có: 

+) Do M(x;y) ∈ d nên ta có 2x - 5y + 3 = 0 ⇔ -2x' + 5y' + 3 = 0 ⇔ 2x' - 5y' - 3 = 0.

+) Do M'(x';y') ∈ d' nên d' có PT là 2x - 5y - 3 = 0.

Cách 3:

Chú ý công thức nhanh: Trong mp Oxy, cho d: Ax + By + C = 0.

Nếu Q_(O,α)(d) = d' và α = π + k2π, O ∉ d thì d' có PT là: Ax + By - C = 0.

+) Do d: 2x - 5y + 3 = 0 và Q_(O,180°)(d) = d' nên d' có PT là 2x - 5y - 3 = 0.

C. Bài tập trắc nghiệm

Câu 1. Trong mặt phẳng Oxy, cho đường thắng d: 2x - 5y + 3 = 0. Viết phương trình đường thẳng d' là ảnh của đường thẳng d qua phép quay tâm I(-1;2), góc quay -180°.

A. 2x - 5y-21 = 0.

B. 2x + 5y + 21 = 0.

C. 2x - 5y + 21 = 0.

D. 3x - 5y + 21 = 0.

Câu 2. Trong mặt phẳng với hệ tọa độ0xy, phép quay tâm I(4;-3) góc quay 180° biến đường thẳng d: x + y - 5 = 0 thành đường thẳng d' có phương trình

A. x - y + 3 = 0.

B. x + y + 3 = 0.

C. x + y + 5 = 0.

D. x + y - 3 = 0.

Câu 3. Trong hệ tọaTrong mặt phẳng Oxy, cho đường tròn (C): x² + y² - 4x + 6y - 12 = 0. Tìm ảnh của đường tròn (C) qua phép quay tâm A(1;-5), góc quay -180°.

A. x² + (y + 7)² = 25.

B. x² + (y + 7)² = 5.

C. x² + (y - 7)² = 25.

D. (x + 7)² + y² = 25.

Câu 4. Gọi d’ là hình ảnh của d qua tâm I góc quay φ (biết I không nằm trên d), đường thẳng d’ song với d khi:

A. 360°.

B. -360°.

C. 180°.

D. -180°.

Câu 5. Cho hình chữ nhật có O là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm O góc α, 0 ≤ α < 2π biến hình chữ nhật trên thành chính nó?

A. Không có.

B. Bốn.

C. Hai.

D. Ba.

Câu 6. Chọn 12 giờ làm mốc, khi kim giờ chỉ một giờ đúng thì kim phút đã quay được một góc bao nhiêu độ?

A. 360°.

B. -360°.

C. 180°.

D. -180°.

Câu 7. Trong mặt phẳng Oxy, cho các điểm A(3;5). Tìm ảnh của điểm A qua phép Quay tâm O góc quay 180°

A. A’(-3;-5)

B. A’(3;-5)

C. A’(-3;5)

D. A’(-5;-3)

Câu 8. Trong mặt phẳng Oxy, cho các điểm A(-4;-8). Tìm ảnh của điểm A qua phép Quay tâm O góc quay -180°

A. A’(4;-8)

B. A’(4;8)

C. A’(8;4)

D. A’(-8;-4)