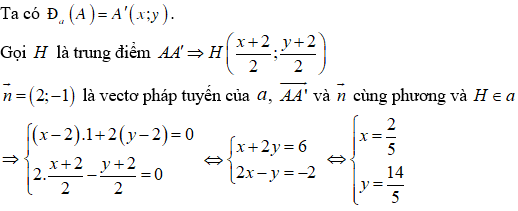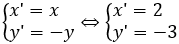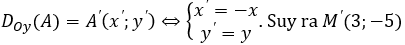Tìm ảnh của một điểm qua phép đối xứng trục cực hay

A. Phương pháp giải

Biểu thức tọa độ:

Trong hệ trục tọa độ Oxy

B. Ví dụ minh họa

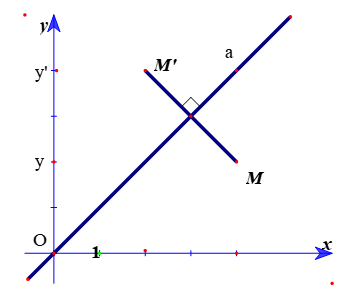
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho phép đối xứng trục Đ_a, với a là đường thẳng có phương trình: 2x - y = 0. Lấy A(2;2); tìm ảnh của A qua phép đối xứng trục a.

Hướng dẫn giải:

Ví dụ 2: Trong mặt phẳng tọa độ Oxy cho điểm M(2;3). Tìm ảnh của điểm M qua phép đối xứng trục Ox.

Hướng dẫn giải:

Biểu thức tọa độ qua phép đối xứng trục Ox:

Với mỗi M(x;y) gọi M' = D_Ox(M) = (x';y') thì 

Ví dụ 3: Trong mặt phẳng tọa độ Oxy cho điểm A(3;5). Tìm ảnh của điểm M qua phép đối xứng trục Ox.

Hướng dẫn giải:

Ta có: 

C. Bài tập trắc nghiệm

Câu 1. Trong mặt phẳng Oxy, cho điểm M(2;3). Hỏi M là ảnh của điểm nào trong các điêm sau qua phép đối xứng trục Oy?

A. (3;2)

B. (2;-3)

C. (3;-2)

D. (-2;3)

Câu 2. Trong mặt phẳng Oxy, cho điêm M(2;3). Hỏi trong trong các điểm sau, điểm nào là ảnh của M qua phép đôi xứng qua đường thắng d:x - y = 0?

A. (3;2)

B. (2;-3)

C. (3;-2)

D. (-2;3)

Câu 3. Trong mặt phẳng tọa độ Oxy, nếu phép đối xứng trục biến điểm M(2;3) thành M'(3;2) thì nó biến điểm C(1;-6) thành điểm:

A. C'(4;16).

B. C'(1;6).

C. C'(-6;-1).

D. C'(-6;1).

Câu 4. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A(1;5), B(-1;2), C(6;-4). Gọi G là trọng tâm của tam giác ABC. Phép đối xứng trục D_Oy biến điểm G thành điểm G' có tọa độ là:

A. (-2;-1).

B. (2;-4).

C. (0;-3).

D. (-2;1).

Câu 5. Trong mặt phẳng tọa độ Oxy, phép đối xứng trục biến điểm A(2;1) thành A'(2;5) có trục đối xứng là:

A. Đường thẳng y = 3.

B. Đường thẳng x = 3.

C. Đường thẳng y = 6.

D. Đường thẳng x + y - 3 = 0.

Câu 6. Trong mặt phẳng tọa độ Oxy, cho hai điểm M(1;3) và M'(-1;1).Phép đối xứng trục Đ_a biến điểm M thành M'. Khi đó trục a có phương trình:

A. x - y + 2 = 0.

B. x - y - 2 = 0.

C. x + y + 2 = 0.

D. x + y - 2 = 0.

Câu 7. Trong mặt phẳng với hệ trục tọa độ Oxy, cho phép đối xứng trục Ox, với M(x;y) gọi M'là ảnh của M qua phép đôi xứng trục Ox. Khi đó tọa độ điềm M'là:

A. M'(x;y)

B. M'(-x;y)

C. M'(-x;-y)

D. M'(x;-y)

Câu 8. Trong mặt phẳng với hệ trục tọa độ Oxy, cho phép đối xứng trục Oy, với M(x;y) gọi M'là ánh của M qua phép đối xứng trục Oy Khi đó tọa độ điềm M'là:

A. M'(x;y)

B. M'(-x;y)

C. M'(-x;-y)

D. M'(x;-y)

Câu 9. Trong mặt phẳng Oxy, ảnh của điểm M(-2;3) qua phép đối xứng trục Δ: x + y = 0 là

A. M'(3;2).

B. M'(-3;-2).

C. M'(3;-2).

D. M'(-3;2).

Câu 10. Trong mặt phẳng tọa độ Oxy, qua phép đối xứng trục Oy, điểm A(3;5) biến thành điểm nào trong các điểm sau?

A. A₁'(3;5).

B. A₂'(-3;5).

C. 3y' - 4x' + 5 = 0.

D. A₄'(-3;-5).