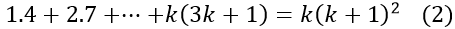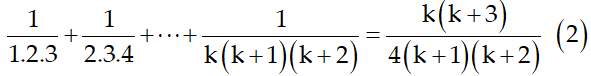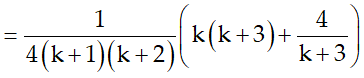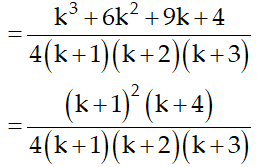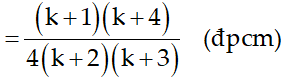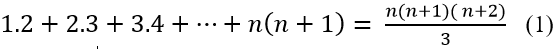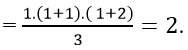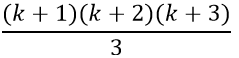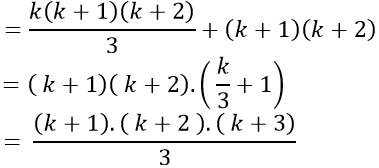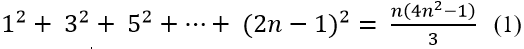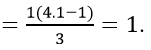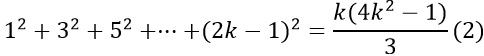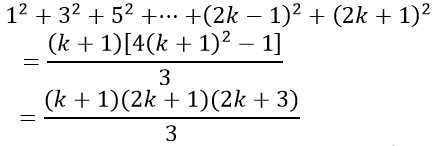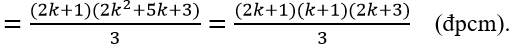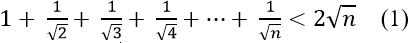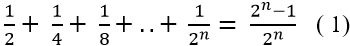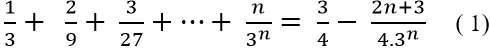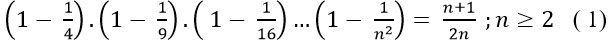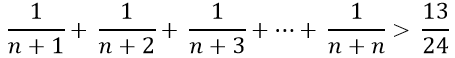Cách chứng minh bằng phương pháp quy nạp cực hay có lời giải

A. Phương pháp giải

Để chứng minh một mệnh đề P(n) phụ thuộc vào số tự nhiên n đúng với mọi n ≥ m (m là số tự nhiên cho trước), ta thực hiện theo hai bước sau:

Bước 1: Chứng minh rằng P(n) đúng khi n = m.

Bước 2: Với k là một số tự nhiên tùy và k ≥ m. Giả sử P(n) đúng khi n = k, ta sẽ chứng minh P(n) cũng đúng khi n= k + 1.

Theo nguyên lý quy nạp toán học, ta kết luận rằng P(n) đúng với mọi số tự nhiên n ≥ m

B. Ví dụ minh họa

Ví dụ 1: Với mỗi số nguyên dương n, gọi u_n = 9ⁿ − 1. Chứng minh rằng với mọi số nguyên dương n thì u_n luôn chia hết cho 8.

Hướng dẫn giải:

+ Với n = 1 ta có u₁ = 9¹ − 1 = 8 chia hết cho 8 (đúng).

+ Giả sử u_k = 9^k − 1 chia hết cho 8 với k ∈ N*

Ta cần chứng minh: u_{k + 1} = 9^k + 1 − 1 chia hết cho 8.

* Thật vậy, ta có u_k+1=9^k+1 − 1 = 9.9^k − 1 = 9(9^k − 1) + 8 = 9u_k + 8.

Vì 9u_k và 8 đều chia hết cho 8

=> u_{k+ 1} = 9^k + 8 ⋮ 8.

Vậy với mọi số nguyên dương n thì u_n chia hết cho 8.

Ví dụ 2: Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta luôn có: 2n + 1 > 2n+ 3 (*)

Hướng dẫn giải:

+ Với n = 2 ta có : 2^{2 + 1} = 8 và 2.2+ 3= 7

=> 8 > 7 nên (*) đúng khi n = 2

+ Giả sử với n = k; k ≥ 2 thì (*) đúng, có nghĩa ta có: 2^{k+ 1} > 2k + 3 (1).

Ta phải chứng minh (*) đúng với n= k + 1, có nghĩa ta phải chứng minh:

2^k+2 > 2(k+1)+3

* Thật vậy, nhân hai vế của (1) với 2 ta được:

2.2^k+1 > 2(2k+3) ⇔ 2^k+2 > 4k + 6 > 2(k + 1) + 3

Vậy 2^k+2 > 2(k+1)+3 (đúng).

Do đó theo nguyên lí quy nạp, (*) đúng với mọi số nguyên dương n ≥ 2

Ví dụ 3: Chứng minh rằng với mọi số nguyên dương n, ta có: 1.4 + 2.7 + ... + n(3n + 1) = n(n + 1)² (1)

Hướng dẫn giải:

+ Với n = 1 ta có:

Vế trái = 1. 4= 4.

Vế phải = 1.(1+ 1)² = 4.

=> Vế trái = Vế phải. Vậy (1) đúng với n = 1.

+ Giả sử (1) đúng với n=k; k ∈ N*; tức là ta có:

1.4+2.7+⋅⋅⋅+k(3k+1)=k(k+1)² (2)

Ta chứng minh nó cũng đúng với n= k+1. Có nghĩa ta phải chứng minh:

1.4+2.7+⋅⋅⋅+k(3k+1)+(k+1)(3k+4)=(k+1)(k+2)²

+ Thật vậy do 1.4+ 2.7+ ...+ k. ( 3k+ 1) = k( k+1)² nên

1.4+2.7+⋯+k( 3k+1)+( k+1).(3k+4)=k(k+1)²+(k+1)(3k+4)

= k( k²+2k+ 1)+ 3k² + 4k+ 3k+ 4

= k³ + 2k² + k+3k² + 7k+ 4 = k³ + 5k² + 8k+ 4 = (k + 1).(k + 2)²

Do đó (1) đúng với mọi số nguyên dương n.

Ví dụ 4: Chứng ming rằng với mọi số nguyên dương n ta có :

Hướng dẫn giải:

+ Với n = 1:

Vế trái 

Vế phải 

=> Vế trái = Vế phải. Vậy (1) đúng với n = 1.

+ Giả sử (1) đúng với n= k; k ∈ N*. Có nghĩa là ta có:

* Ta phải chứng minh (1) đúng với n= k+ 1. Có nghĩa ta phải chứng minh:

* Thật vậy

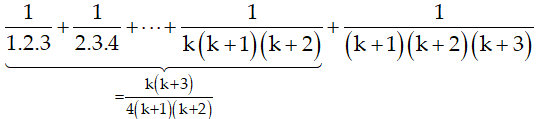
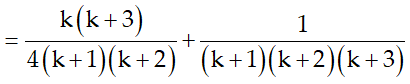
Vậy (1) đúng khi n= k+ 1. Do đó (1) đúng với mọi số nguyên dương n.

Ví dụ 5: Chứng minh với mọi số nguyên dương n và n ≥ 5 thì 2ⁿ > n² (*)

Hướng dẫn giải:

* Với n = 5 ta có: 2⁵ > 5² ( vì 32 > 25) (đúng).

Vậy (*) đúng với n = 5.

* Giả sử với n= k; k ≥ 5 thì (*) đúng, có nghĩa ta có: 2^k > k² (1).

Ta phải chứng minh (*) đúng với n = k + 1, có nghĩa ta phải chứng minh: 2^k+1 > (k+1)²

* Thật vậy, nhân hai vế của (1) với 2 ta được:

2. 2^k > 2.k² ⇔ 2^k+1 > k² + k²

⇔ 2^k+1 > k² + 2k + 1= (k+1)² (vì k² > 2k+ 1 với mọi k ≥ 5) .

Vậy (*) đúng với mọi số nguyên dương n≥5.

Ví dụ 6: Chứng minh với mọi số nguyên n ta có:

Hướng dẫn giải:

* Với n = 1:

Vế trái của (1) = 1. 2= 2, vế phải của (1) 

Suy ra (1) đúng với n= 1.

* Giả sử (1) đúng với n= k; k∈N*.Có nghĩa là ta có:

1.2+2.3+3.4+⋅⋅⋅+k(k+1)=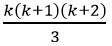 (2)

*Ta phải chứng minh (1) đúng với n= k+ 1. Có nghĩa ta phải chứng minh:

1.2+2.3+3.4+⋅⋅⋅+k(k+1)+(k+1)(k+2)=

Thật vậy:

1.2+2.3+3.4+⋅⋅⋅+k(k+1)+(k+1)(k+2)

Vậy (1) đúng khi n= k+ 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Ví dụ 7: Chứng minh rằng với mọi số nguyên dương n ta có:

Hướng dẫn giải:

* Với n = 1:

Vế trái của (1) = 1 và vế phải của (1) 

Vậy (1) đúng với n = 1.

* Giả sử (1) đúng với n= k; k ∈ N*. Có nghĩa là ta có:

Ta chứng minh (1) đúng với n= k+ 1. Có nghĩa ta phải chứng minh:

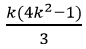
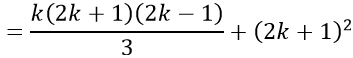
* Thật vậy 1²+3²+5²+⋅⋅⋅+(2k − 1)²+(2k+1)² =  + (2k+1)² (thế (2) vào).

Vậy (1) đúng khi n= k+ 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Ví dụ 8: Chứng minh rằng với mọi số nguyên dương n ta có:

1.2 + 2.5 + 3.8+ ..+ n(3n − 1) = n²(n+1) (1)

Hướng dẫn giải:

* Với n = 1:

Vế trái của (1) = 2, vế phải của (1)= 12.( 1+ 1)= 2.

Suy ra (1) đúng với n = 1.

* Giả sử (1) đúng với n= k; k ∈ N*. Có nghĩa là ta có:

1.2 + 2.5 + 3.8 +⋅⋅⋅+ k(3k − 1) = k²(k+1) (2)

Ta phải chứng minh (1) đúng với n = k+1. Có nghĩa ta phải chứng minh:

1.2 + 2.5 + 3.8 +⋅⋅⋅+ k(3k − 1) + (k+1)(3k+2) = (k+1)²(k+2)

Thật vậy:

1.2 + 2.5 + 3.8 +⋅⋅⋅+ k(3k − 1) + (k + 1)(3k + 2) = k²(k+1) + (k + 1)(3k + 2)

= (k + 1)(k² + 3k + 2) = (k + 1)(k + 1)(k + 2) = (k+1)²(k+2) (đpcm).

Vậy (1) đúng khi n = k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Ví dụ 9: Chứng minh với mọi số nguyên n và n ≥ 3 thì 3ⁿ > n² + 4n + 5 (*)

Hướng dẫn giải:

* Với n = 3 ta có 3³ > 3² + 4.3 + 5 ⇔ 27 > 26 (đúng).

Vậy (*) đúng với n = 3.

* Giả sử với n = k ; k ≥ 3 thì (*) đúng, có nghĩa ta có: 3^k > k² + 4k + 5 (1).

Ta phải chứng minh (*) đúng với n = k+ 1, có nghĩa ta phải chứng minh:

3^{k + 1} > (k+1)² + 4(k+1) + 5

* Thật vậy, nhân hai vế của (1) với 3 ta được: 3.3^k > 3.k² + 12k + 15

⇔ 3^{k + 1} > (k² + 2k + 1) + 4(k+1)+ 5 + (2k² + 6k + 5) (2)

Vì (2k² + 6k + 5) > 0 với mọi k ≥ 3 (3)

Từ (2) và (3) suy ra: 3^k+1 > (k² + 2k + 1) + 4(k + 1) + 5

Hay 3^k+1 > (k+1)² + 4(k+1) + 5

Vậy (*) đúng với mọi số nguyên dương n ≥ 3.

Ví dụ 10: Chứng minh với mọi số nguyên dương n ta có: n³ − n chia hết cho 3

Hướng dẫn giải:

Đặt u_n = n³ − n

* Ta có u₁ = 1³ − 1 = 0 chia hết cho 3

=> đúng với n = 1.

* Giả sử u_k = k³ − k chia hết cho 3.

Ta cần chứng minh u_k+1 = (k + 1)³ − (k + 1) chia hết cho 3.

* Thật vậy, u_k+1 = k³+ 3k² + 3k + 1 − k − 1 = k³ + 3k² + 2k

⇔ u_{k + 1} = (k³ − k) + (3k² + 3k) = u_k +3(k² + k)

Vì u_k và 3(k² + k) đều chia hết cho 3, nên u_k+1 cũng chia hết cho 3.

Vậy với mọi số nguyên dương n thì un chia hết cho 3.

Ví dụ 11: Chứng minh rằng với mọi số nguyên dương n ta có: 2n³ − 3n² + n chia hết cho 6.

Hướng dẫn giải:

* Đặt u_n = 2n³ − 3n² + n

*Ta có: u₁ = 2. 1³ − 3 . 1² + 1 = 0 chia hết cho 6

=> đúng với n = 1.

* Giả sử u_k = 2k³ − 3k²+ k chia hết cho 6.

Ta cần chứng minh: u_{k + 1} = 2.(k+1)³ − 3.(k+1)² + k+1 chia hết cho 6.

* Thật vậy ta có: u_k+1 = 2.k³+ 6k² + 6k + 2 − 3k² − 6k − 3 + k + 1

⇔ u_{k + 1} = 2k³ + 3k² + k = 2k³ − 3k² + k + 6k² = u_k + 6k²

Vì u_k và 6k² đều chia hết cho 6, nên u_{k + 1} cũng chia hết cho 6.

Vậy với mọi số nguyên dương n thì u_n chia hết cho 6.

Ví dụ 12: Chứng minh với mọi số nguyên dương n ta có: 13ⁿ − 1 chia hết cho 6.

Hướng dẫn giải:

* Đặt u_n = 13ⁿ − 1

* Với n = 1, ta có u₁ = 13¹ − 1 = 12 chia hết cho 6

=> đúng với n = 1.

* Giả sử u_k = 13^k − 1 chia hết cho 6 (với k ∈ N*).

Ta cần chứng minh: u_k+1= 13^k+1 − 1 ⋮ 6 .

* Thật vậy ta có: u_k+1 = 13 . 13^k − 1 = 13(13^k − 1) + 12 = 13.u_k + 12

Vì 13u_k và 12 đều chia hết cho 6, nên u_{k + 1} cũng chia hết cho 6.

Vậy với mọi số nguyên dương n thì u_n chia hết cho 6.

C. Bài tập vận dụng

Câu 1: Chứng minh với mọi số nguyên dương n ta có:

Câu 2: Chứng minh với mọi số nguyên dương n ta có:

Câu 3: Chứng minh với mọi số nguyên dương n ta có:

Câu 4: Chứng minh với mọi số nguyên n thì n³ + 11n chia hết cho 6.

Câu 5: Chứng minh với mọi số nguyên dương n thì 4ⁿ + 6n + 8 chia hết cho 9

Câu 6: Chứng minh với mọi số nguyên dương n ta có: 7.2^{2n − 2} + 3^{2n − 1} chia hết cho 5?

Câu 7: Chứng minh với mọi n nguyên và n ≥ 4 ta có: 3^{n − 1} > n(n+ 2) (1)

Câu 8: Chứng minh với mọi số nguyên dương n ta có: n³ + 3n² + 5n chia hết cho 3.

Câu 9: Chứng minh với mọi số nguyên dương n ta có: 4ⁿ + 15n − 1 chia hết cho 9

Câu 10: Chứng minh với mọi số nguyên dương n ta có:

1.2.3 + 2.3.4 + 3.4.5 + ..+ n(n+1).(n+2) = 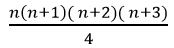 (1)

Câu 11: Chứng minh với mọi số nguyên dương n ≥ 2 ta có:

Câu 12: Chứng minh với mọi số nguyên n và n ≥ 2 ta có :

Câu 13: Chứng minh với mọi số nguyên dương n ta có: nⁿ ≥ (n+1)^{n − 1} ( 1)