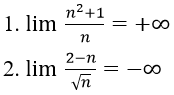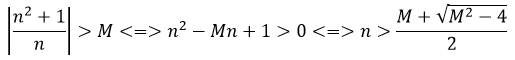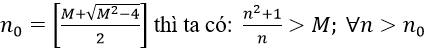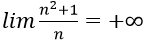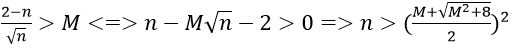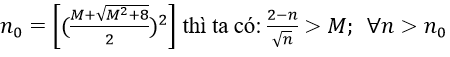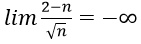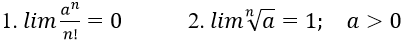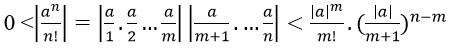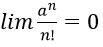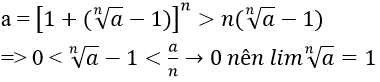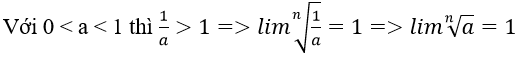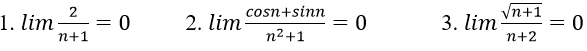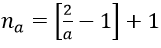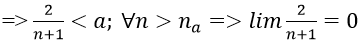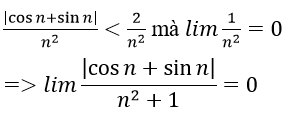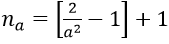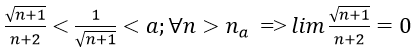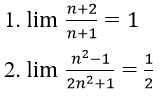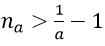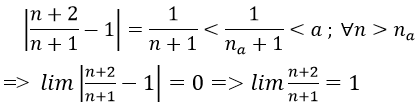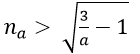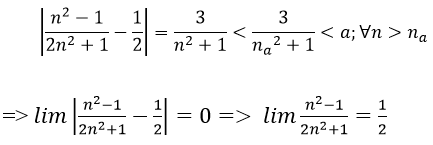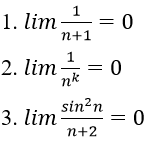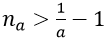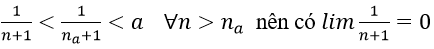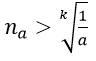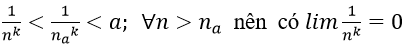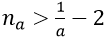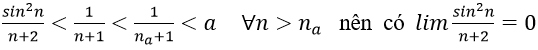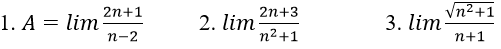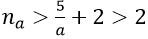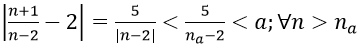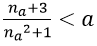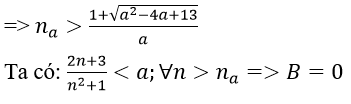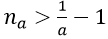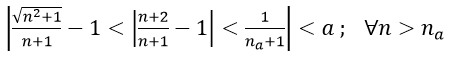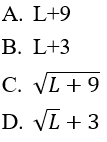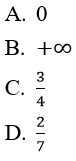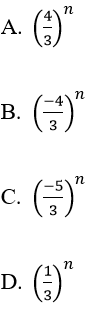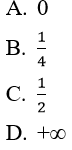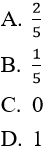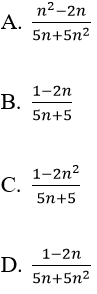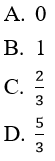Cách tìm giới hạn của dãy số bằng định nghĩa cực hay

A. Phương pháp giải & Ví dụ

- Để chứng minh limu_n = 0 ta chứng minh với mọi số a > 0 nhỏ tùy ý luôn tồn tại một số n_a sao cho |u_n| n_a.

- Để chứng minh limu_n = 1 ta chứng minh lim(u_n-1) = 0.

- Để chứng minh limu_n = +∞ ta chứng minh với mọi số M > 0 lớn tùy ý, luôn tồn tại số tự nhiên n_M sao cho u_n > M ∀n > n_M.

- Để chứng minh limu_n = -∞ ta chứng minh lim(-u_n) = +∞

- Một dãy số nếu có giới hạn thì giới hạn đó là duy nhất.

Ví dụ minh họa

Bài 1: Chứng minh các giới hạn sau:

Hướng dẫn:

1. Với mọi số thực dương M lớn tùy ý, ta có:

Ta chọn 

Do đó: 

2. Với mọi M > 0 lớn tùy ý, ta có:

Ta chọn 

Do đó: 

Bài 2: Chứng minh rằng dãy số (u_n): u_n = (-1)ⁿ không có giới hạn.

Hướng dẫn:

Ta có: u_2n → +∞; u_(2n+1) = -(2n+1) → -∞

Do đó dãy số đã cho không có giới hạn.

Bài 3: Chứng minh các giới hạn sau:

Hướng dẫn:

1. Gọi m là số tự nhiên thỏa: m+1 > |a|. Khi đó với mọi n > m+1

Ta có:

Mà 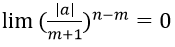 Từ đó suy ra: 

2. Nếu a = 1 thì ta có đpcm

+ Giả sử a > 1. Khi đó:

+ 

Tóm lại ta luôn có: 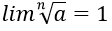 với a > 0.

Bài 4: Chứng minh các giới hạn sau

Hướng dẫn:

1. Với mọi a > 0 nhỏ tùy ý, ta chọn 

2. Ta có

3. Với mọi số thực a > 0 nhỏ tùy ý, ta chọn 

Ta có:

Bài 5: Chứng minh rằng:

Hướng dẫn:

1. Với a > 0 nhỏ tùy ý, ta chọn 

Ta có:

2. Với a > 0 nhỏ tùy ý, ta chọn 

Ta có:

Bài 6: Chứng minh rằng:

Hướng dẫn:

1. Với a > 0 nhỏ tùy ý, ta chọn 

Ta có:

2. Với a > 0 nhỏ tùy ý, ta chọn 

Ta có:

3. Với a > 0 nhỏ tùy ý, ta chọn 

Ta có:

Bài 7: Chứng minh rằng dãy số (u_n ) : u_n = (-1)ⁿ không có giới hạn.

Hướng dẫn:

Ta có: u_2n = 1 ⇒ limu_2n = 1; u_(2n+1) = -1 ⇒ limu_(2n+1) = -1

Vì giới hạn của dãy số nếu có là duy nhất nên ta suy ra dãy (u_n) không có giới hạn.

Bài 8: Dùng định nghĩa tìm các giới hạn sau :

Hướng dẫn:

1. Với số thực a > 0 nhỏ tùy ý, ta chọn 

Ta có: 

Vậy A = 2

2. Với số thực a > 0 nhỏ tùy ý, ta chọn n_a thỏa mãn 

3. Với số thực a > 0 nhỏ tùy ý, ta chọn 

Ta có:

Vậy C = 1

B. Bài tập vận dụng

Bài 1: 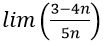 có giá trị bằng:

Bài 2: Dãy số nào sau đây có giưới hạn là +∞ ?

A. u_n = 9n² - 2n⁵

B. u_n = n⁴ - 4n⁵

C. u_n = 4n² - 3n

D. u_n = n³ - 5n⁴

Bài 3: Nếu limu_n = L, u_n + 9 > 0 ∀n thì 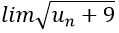 bằng số nào sau đây?

Bài 4: 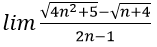 bằng:

A. 0         B.1         C. 2          D. +∞

Bài 5: 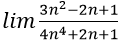 bằng:

Bài 6: 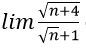 có giá trị bằng:

Bài 7: Dãy số nào sau đây có giới hạn khác 0 ?

Bài 8: Dãy số nào sau đây có giới hạn bằng 0 ?

Bài 9: 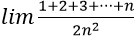 bằng:

Bài 10: 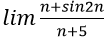 bằng:

Bài 11: 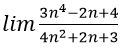 bằng:

Bài 12: Dãy số nào sau đây có giưới hạn bằng 1/5 ?

Bài 13: 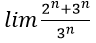 có giá trị bằng:

Bài 14: lim⁡(-3n³ + 2n² - 5) bằng:

A. -3         B.0         C. -∞          D. +∞

Bài 15: Lim( 2n⁴ + 5n² - 7n ) bằng:

A. -∞         B.0         C. 2          D. +∞