Cách giải bài tập về Hai qui tắc đếm cơ bản cực hay, chi tiết

1. Hai quy tắc đếm cơ bản

a) Quy tắc cộng

● Định nghĩa: Một công việc nào đó có thể được thực hiện theo một trong hai phương án A hoặc

B. Nếu phương án A có m cách thực hiện, phương án B có n cách thực hiện và không trùng với bất kì cách nào trong phương án A thì công việc đó có m + n cách thực hiện.

● Công thức quy tắc cộng:

Nếu các tập A₁, A₂, A₃,…., A_n đôi một rời nhau. Khi đó

|A₁ ∪ A₂ ∪ A₃ ∪ ... ∪ A_n⁡ | = |A₁| + |A₂| + |A₃| + .... + |A_n|

Ví dụ minh họa

Ví dụ 1. Đi từ thủ đô Hà Nội đến thành phố Đà Nẵng có thể đi bằng ô tô, tàu hỏa và máy bay. Biết rằng có 20 chuyến xe ô tô, 10 chuyến tàu hỏa và 5 chuyến máy bay khởi hành. Hỏi có bao nhiêu cách đi từ thủ đô Hà Nội đến thành phố Đà Nẵng.

Hướng dẫn

C. ba phương án để chọn phương tiện đi từ Hà Nội đến Đà Nẵng là: ô tô, tàu hỏa và máy bay.

+ Có 20 cách chọn để đi bằng xe ô tô (có 20 chuyến xe ô tô)

+ Có 10 cách chọn để đi bằng tàu hỏa (có 10 chuyến tàu hỏa)

+ Có 5 cách chọn để đi bằng máy bay (có 5 chuyến máy bay)

Vậy có tất cả: 20 + 10 + 5 = 35 cách chọn.

Ví dụ 2. Trường THPT Bắc Đông Quan cần cử một học sinh đi tham dự đại hội đoàn cấp huyện. Nhà trường quyết định chọn một học sinh giỏi trong lớp 11A hoặc lớp 11K. Hỏi nhà trường có bao nhiêu cách chọn, biết rằng lớp 11A có 10 học sinh giỏi và lớp 11K có 15 học sinh giỏi?

Hướng dẫn

Nhà trường có hai phương án chọn.

- Phương án thứ nhất là chọn một học sinh giỏi trong lớp 11A, phương án này có 10 cách chọn (do lớp 11A có 10 bạn học sinh giỏi).

- Phương án thứ hai là chọn một học sinh trong lớp 11K, phương án hai này có 15 cách chọn (do lớp 11K có 15 học sinh giỏi).

Áp dụng quy tắc cộng, vậy nhà trường có: 10 + 15 = 25 cách chọn.

b) Quy tắc nhân

● Định nghĩa: Một công việc nào đó có thể bao gồm hai công đoạn A và

B. Nếu công đoạn A có m cách thực hiện và ứng với mỗi cách đó có n cách thực hiện công đoạn B thì công việc đó có m.n cách thực hiện.

● Công thức quy tắc nhân:

Nếu các tập A₁, A₂, A₃,…., A_n đôi một rời nhau. Khi đó

|A₁ ∩ A₂ ∩ A₃ ∩ ... ∩ A_n| = |A₁|.|A₂|.|A₃|...|A_n|

Ví dụ minh họa

Ví dụ 1. Biển số xe máy của thành phố Hà Nội (không kể mã thành phố) có 6 kí tự, trong đó kí tự ở vị trí đầu tiên là một chữ cái (trong bảng 26 chữ cái Tiếng Anh), kí tự thứ hai là một số thuộc tập {1; 2; 3…; 9}, mỗi kí tự ở 4 vị trí tiếp theo thuộc tập {0; 1; 2; 3…; 9}. Hỏi nếu chỉ dùng một mã số thành phố thì thành phố Hà Nội có thể làm được nhiều nhất bao nhiêu biển số xe máy khác nhau?

Hướng dẫn

+ Ta có 26 cách chọn chữ cái để xếp ở vị trí đầu tiên. (vì có 26 chữ cái).

+ Tương tự có 9 cách chọn cho vị trí thứ hai (tập {1; 2; 3…; 9} có 9 số)

+ Có 10 cách chọn số cho mỗi vị trí trong 4 vị trí sau (tập {0; 1; 2; 3…; 9} có 10 số)

Theo quy tắc nhân, vậy có 26.9.10.10.10.10 = 2340000 (biển số xe).

Ví dụ 2. Minh muốn qua nhà Kiên để cùng Kiên qua nhà Nam chơi. Từ nhà Minh đến nhà Kiên có 5 con đường đi, từ nhà Kiên tới nhà Nam có 8 con đường đi. Hỏi Minh có bao nhiêu cách chọn đường đi đến nhà Nam.

Hướng dẫn

Với mỗi cách đi từ nhà Minh đến nhà Kiên sẽ có 8 cách đi tiếp tới nhà Nam. Vì có 5 cách đi từ nhà Minh đến nhà Kiên, do đó theo quy tắc nhân, có tất cả 5.8 = 40 cách đi từ nhà Minh đến nhà Nam.

2. Một số dạng bài toán đếm cơ bản

a) Dạng 1: Đếm số phương án liên quan đến số tự nhiên

● Phương pháp:

- Sử dụng các quy tắc cộng và quy tắc nhân.

- Sử dụng các kiến thức liên quan đến số tự nhiên: Số chẵn, số lẻ, tính chia hết,…

● Ví dụ minh họa:

Ví dụ 1. Từ các chữ số 1, 2, 3 có thể lập được bao nhiêu số tự nhiên khác nhau và mỗi số có các chữ số khác nhau:

A. 15

B. 20

C. 72

D. 36

Hướng dẫn

TH1: Lập số có 1 chữ số, có 3 số là 1, 2 và 3

TH2: Lập số có hai chữ số và mỗi số có các chữ số khác nhau

Gọi số đó là 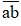, (a, b ∈ {1; 2; 3} và a ≠ b)

+ Chọn a: a ∈ {1; 2; 3}, a có 3 cách chọn

+ Chọn b: b ∈ {1; 2; 3} \ {a}, b có 2 cách chọn

Theo quy tắc nhân, vậy có 3.2 = 6 số có hai chữ số khác nhau

TH3: Lập số có ba chữ số và mỗi chữ số khác nhau

Gọi số đó là 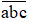, (a, b, c ∈ {1; 2; 3} và a ≠ b ≠ c)

+ Chọn a: a∈{1; 2; 3} , a có 3 cách chọn

+ Chọn b: b∈{1; 2; 3}\{a}, b có 2 cách chọn

+ Chọn c: c∈{1; 2; 3}\{a; b}, c có 1 cách chọn

Theo quy tắc nhân, vậy có 3.2.1 = 6 số có ba chữ số khác nhau

Theo quy tắc cộng, vậy có tất cả: 3 + 6 + 6 = 15 số

Đáp án A

Ví dụ 2. Từ các chữ số 1, 2, 3, 4, 5, 6, 7 lập được bao nhiêu số có 4 chữ số khác nhau và là số chẵn.

A. 360

B. 343

C. 523

D. 347

Hướng dẫn

Gọi số cần lập là 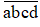; a, b, c, d {1, 2, 3, 4, 5, 6, 7} và a, b, c, d khác nhau từng đôi một.

Công việc ta cần thực hiên là lập số x = 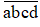 thỏa mãn x là số chẵn nên d phải là chữ số chẵn. Do đó để thực hiện công việc này, ta thực hiện qua các công đoạn sau:

+ Chọn d: vì d là số chẵn nên d chỉ có thể là các số 2, 4, 6, nên có 3 cách chọn d

+ Chọn a: vì ta đã chọn d nên a chỉ có thể là một trong các số của tập {1, 2, 3, 4, 5, 6, 7}\ {a}, vậy a có 6 cách chọn.

+ Chọn b, tương tự, trừ đi a và d, có 5 cách chọn b

+ Tương tự, chọn c có 4 cách chọn.

Vậy theo quy tắc nhân ta có: 3.6.5. 4 = 360 số chẵn

Đáp án A

Ví dụ 3. Từ các chữ số 0, 1, 2, 3, 4, 5, 6. Lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhau và chia hết cho 5.

A. 660

B. 432

C. 679

D. 523

Hướng dẫn

Nhắc lại kiến thức: số chia hết cho 5 là số có chữ số tận cùng là 0 và 5.

Gọi số cần tìm 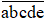, (a; b; c; d; e {0, 1, 2, 3, 4, 5, 6}; a ≠ 0) và a, b, c, d, e khác nhau từng đôi một.

TH1: e = 0, e có 1 cách chọn

a, b, c, d ∈ {1, 2, 3, 4, 5, 6}

Chọn a, có 6 cách chọn

Chọn b có 5 cách chọn

Chọn c có 4 cách chọn

Chọn d có 3 cách chọn

Theo quy tắc nhân, vậy có: 1.6.5.4.3 = 360 số

TH2: e = 5, có 1 cách chọn e

a ∈ {1, 2, 3, 4, 6}, a có 5 cách chọn

b, c, d ∈ {1, 2, 3, 4, 5, 6} \ {a}, suy ra b có 5 cách chọn, c có 4 cách chọn và d có 3 cách chọn.

Theo quy tắc nhân vậy có: 1.5.5.4.3 = 300 số

Áp dụng quy tắc cộng ta có tất cả: 360 + 300 = 660 số.

Đáp án A

b) Dạng 2: Đếm một số phương án liên quan đến kiến thức thực tế

● Phương pháp giải: Sử dụng các quy tắc cộng, quy tắc nhân

● Ví dụ minh họa

Ví dụ 1. Một người vào một cửa hàng ăn, người đó chọn thực đơn 1 món ăn trong 5 món ăn khác nhau, 1 loại quả tráng miệng trong 5 loại quả tráng miệng khác nhau, 1 loại đồ uống trong 3 loại đồ uống khác nhau. Có bao nhiêu cách chọn 1 thực đơn?

A. 100

B. 13

C. 75

D. 25

Hướng dẫn

+ Người đó chọn 1 món ăn trong 5 món có 5 cách chọn

+ Chọn 1 loại quả tráng miệng trong 5 loại có 5 cách chọn

+ Chọn 1 loại đồ uống trong 3 loại có 3 cách chọn

Vì việc chọn thực đơn bao gồm các công đoạn là chọn món ăn, tráng miêng và nước uống nên theo quy tắc nhân ta có: 5.5.3 = 75 cách chọn thực đơn.

Đáp án C

Ví dụ 2. Trong hộp bút có 4 chiếc bút đen, 5 chiếc bút xanh. Hỏi có bao nhiêu cách chọn 1 chiếc bút bất kỳ?

A. 20

B. 9

C. 1

D. 5

Hướng dẫn

+ Chọn 1 chiếc bút đen có 4 cách chọn

+ Chọn 1 chiếc bút xanh có 5 cách chọn

Việc chọn bút xanh không ảnh hưởng đến việc vậy theo quy tắc cộng ta có 4 + 5 = 9 cách.

Đáp án B