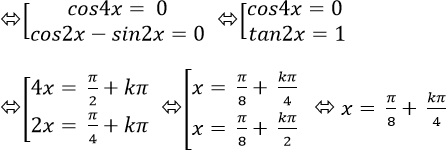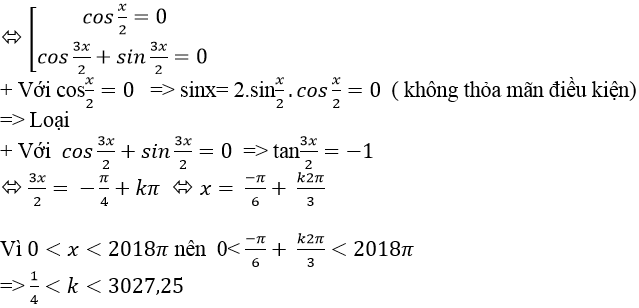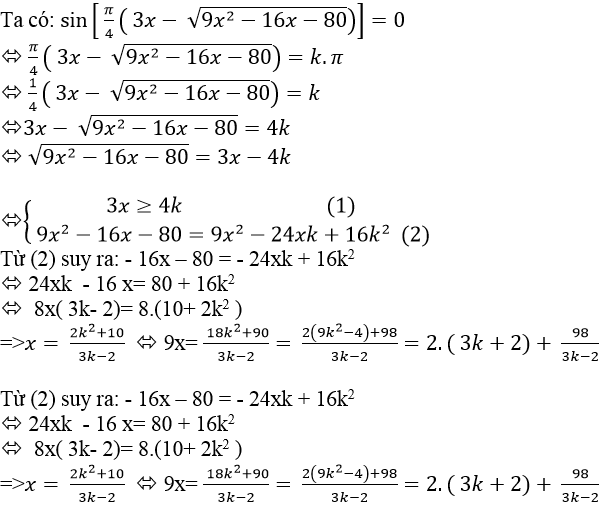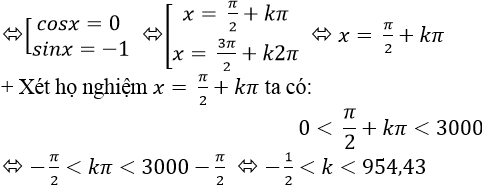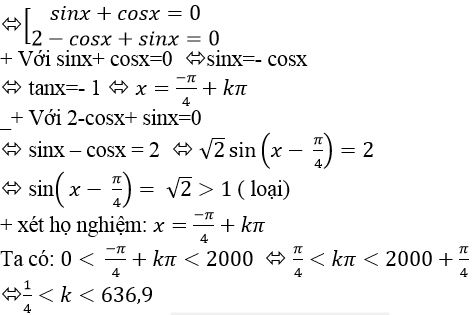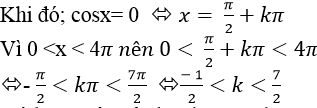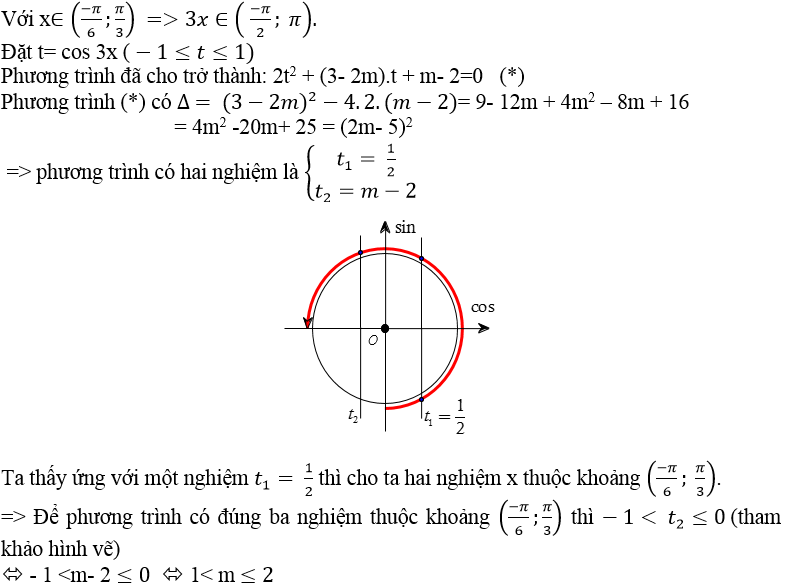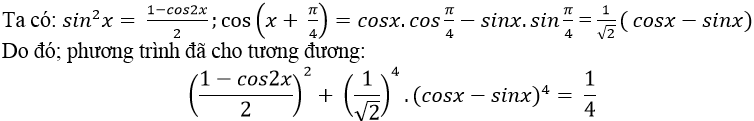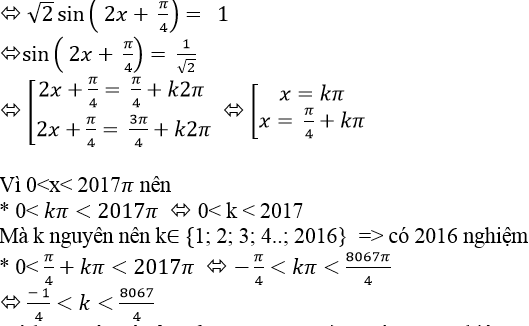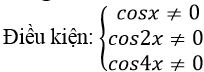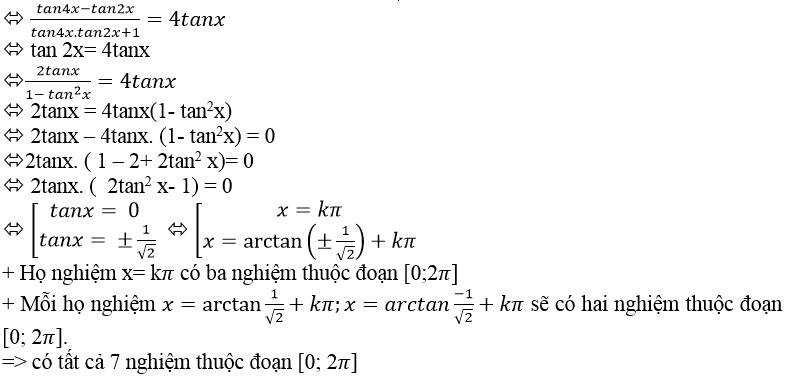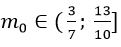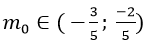Tìm số nghiệm của phương trình lượng giác trong khoảng, đoạn

A. Phương pháp giải

B. Ví dụ minh họa

Ví dụ 1. Phương trình 2cos² x+ 2cos²2x + 2cos²3x – 3= cos4x. (2sin2x+ 1) có bao nhiêu nghiệm thuộc khoảng( 10; 1000) ?

A. 1207

B. 1260

C.1261

D. 1208

Lời giải.

Ta có: 2cos² x+ 2cos²2x + 2cos²3x – 3= cos4x

⇒ 1+ cos2x + 1+ cos4x + 1+ cos6x- 3 = 2.cos4x.sin2x + cos4x

⇒ cos2x+ cos4x+ cos6x = 2cos 4x. sin2x + cos4x

⇒ cos2x+ cos6x – 2cos 4x.sin2x=0

⇒ 2cos 4x. cos2x – 2.cos4x. sin2x= 0

⇒ 2cos 4x.(cos2x – sin2x) = 0

⇒ 12,23 < k < 1272,8

Mà k nguyên nên k∈{ 13;14;…1271;1272}

⇒ có 1260 số thỏa mãn.

Chọn B.

Ví dụ 2. Phương trình 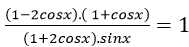 có bao nhiêu nghiệm thuộc khoảng (0; 108π)

A. 3025

B. 3026

C. 3027

D. Tất cả sai

Lời giải.

Điều kiện: ( 1+2cosx).sinx ≠ 0

Với điều kiện trên phương trình trên tương đương:

( 1- 2cosx).( 1+ cosx) = ( 1+ 2cosx). sinx

⇒ 1+ cosx – 2cosx – 2cos² x= sinx + 2sinx. cosx

⇒ 2cos² x – 1 + cosx+ sinx + 2sinx.cosx= 0

⇒ cos2x + cosx + sinx + sin2x=0

Mà k nguyên nên k∈ {1; 2; 3; ..; 3027}

⇒ Phương trình đã cho có 3027 nghiệm.

Chọn C.

Ví dụ 3. Phương trình 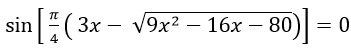 có bao nhiêu nghiệm nguyên dương?

A. 1

B. 2

C.3

D. 4

Lời giải.

Vì x nguyên dương nên (3k- 2)∈Ư (98)={1;2; 7;14;49;98}

Từ đó ta tính được k∈ {1; 3; 17} – chú ý k nguyên.

+ k= 1 ⇒ x= 12

+ k= 3 ⇒ x = 4

+ k= 17 ⇒ x = 12

⇒ Phương trình có hai nghiệm nguyên dương là 12 và 4

Chọn B.

Ví dụ 4. Phương trình 2sin2x+ 4cosx = 0 có bao nhiêu nghiệm trong khoảng (0; 3000)

A. 954

B.955

C. 956

D. 957

Lời giải

Ta có: 2sin2x + 4cosx = 0

⇒ 4. sinx.cos+ 4cosx= 0

⇒ 4cosx. ( sinx+ 1) = 0

Mà k nguyên nên k∈{0;1;2;3;…;954} có 955 giá trị của k thỏa mãn.

⇒ Phương trình có 955 nghiệm thuộc khoảng (0;3000)

Chọn B.

Ví dụ 5. Cho phương trình 2sinx+ 2cosx – cos2x=0. Tìm số nghiệm của phương trình thuộc (0; 2000).

A.624

B. 652

C. 645

D. 636

Lời giải

Ta có: 2sinx+ 2cosx – cos2x = 0

⇒ ( 2sinx+ 2cosx) – (cos² x – sin² x)= 0

⇒ 2(sinx + cosx) - ( cosx- sinx) . ( cosx+ sinx)= 0

⇒ ( sinx+ cosx). ( 2- cosx + sinx) = 0

Mà k nguyên nên k∈{ 1;2;3..;635;636}. Do đó; phương trình đã cho có 636 nghiệm trong khoảng (0; 2000)

Chọn D.

Ví dụ 6. Tìm số nghiệm của phương trình sin(cosx) = 0 trên khoảng (0; 4π) ?

A. 2

B.3

C. 4

D. 5

Lời giải

Ta có: sin(cosx)=0

⇒ cosx = kπ (*)

Do với mọi x ta luôn có: - 1 ≤ cosx ≤ 1 nên từ (*) suy ra: k= 0

Mà k nguyên nên k∈ {0;1; 2;3}.

⇒ Phương trình đã cho có 4 nghiệm trên khoảng (0; 4π)

Chọn C.

Ví dụ 7: Cho phương trình: 2cos²3x + (3- 2m)cos3x + m-2= 0. Tìm tất cả các giá trị thực của m để phương trình có đúng ba nghiệm thuộc khoảng  ?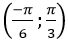

A. 1 < m < 2

B. 2 < m ≤ 3

C. 1 < m ≤ 2

D. 2 < m < 3

Lời giải.

Chọn C.

Ví dụ 8. Phương trình: 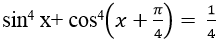 có bao nhiêu nghiệm thuộc khoảng (0; 2017π)

A.4033

B. 4032

C. 4035

D. 4036

Lời giải.

⇒ ( 1- cos2x)² + (cosx- sinx)⁴=1

⇒ 1- 2cos2x + cos²2x + ( cos²x + sin²x – 2.cosx. sinx)²= 1

⇒ 1- 2cos2x + cos²2x + (1- sin2x)² - 1= 0

⇒ - 2cos2x + cos²2x + 1- 2sin2x+ sin²2x = 0

⇒ (cos²2x + sin²2x ) +1 – 2.(cos2x+ sin2x)= 0

⇒ 2- 2(cos2x + sin2x) = 0

⇒ cos2x + sin2x = 1

Mà k nguyên nên k∈{0;1;2; ...; 2016} ⇒ có 2017 nghiệm

Kết hợp 2 trường hợp có 4033 nghiệm trong khoảng đang xét.

Chọn A.

Ví dụ 9. Tìm số nghiệm của phương trình: tan4x – tan2x – 4tanx= 4tan4x. tan2x. tanx trên đoạn [0; 2π]?

A. 6

B. 7

C. 8

D. 9

Lời giải

Ta có: tan4x – tan2x – 4tanx = 4tan4x. tan2x. tanx

⇒ tan4x – tan2x = 4tan4x. tan2x. tanx + 4 tanx

⇒ tan4x - tan2x = 4tanx. (tan 4x. tan2x + 1)

Chọn B.

Ví dụ 10. Tính tổng các nghiệm của phương trình 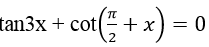 trên khoảng (0; π)?

A. π/4

B. π/3

C. π

D.Đáp án khác

Lời giải

Điều kiện:

Ta có: tan 3x + cot(π/2+x)=0

⇒ tan3x – tanx = 0 ⇒ tan3x= tanx

⇒ 3x = x+kπ ⇒ 2x= kπ

⇒ x= kπ/2 ( không thỏa mãn điều kiện )

Do đó; phương trình đã cho vô nghiệm.

Chọn D.

C. Bài tập vận dụng

Câu 1:Tìm số nghiệm của phương trình: cos²x.(tan² x – cos2x)= cos³x- cos² x+ 1 trên khoảng (0; 6π) ?

A. 9

B. 8

C. 10

D.11

Câu 2:Cho phương trình: m.sin²x – 3sinx.cosx – m- 1 = 0. Gọi S là tập tất cả các giá trị nguyên của m thuộc đoạn [-4; 7] để phương trình có đúng ba nghiệm thuộc (0; 3π/2). Số các phần tử của tập S là:

A. 4

B. 3

C. 5

D. 6

Câu 3:Tìm số nghiệm của phương trình: sinx. cosx + |sinx+cosx|= 1 trên (0; 2π)?

A. 2

B.4

C.3

D.5

Câu 4:Tìm số nghiệm của phương trình 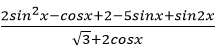 trên đoạn [ 2π;10π]?

A. 6

B .7

C. 8

D. 9

Câu 5:Cho phương trình: ( cosx+ 1).(4cos 2x – m.cosx)= m.sin² x. Số các giá trị nguyên của m để phương trình có đúng hai nghiệm thuộc đoạn [0;2π/3] là:

A. 1

B. 2

C. 3

D. 4

Câu 6:Có bao nhiêu giá trị của m để phương trình: (sinx-1).[2cos²x- ( 2m+1).cosx + m]=0 có đúng bốn nghiệm thuộc đoạn [0; 2π]

A . 1

B. 2

C .3

D .4

Câu 7:Cho phương trình: (cos⁴ x- sin⁴ x).( 2cos2x+5) – 3 = 0. Tìm số nghiệm của phương trình trên khoảng ( π;4π)

A. 5

B. 7

C. 6

D. 8

Câu 8:Tìm số nghiệm của phương trình 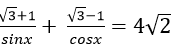 trên đoạn [0;2π]

A.3

B.4

C.5

D. 6

Câu 9:Biết rằng khi m= m₀ thì phương trình : 2sin² x – (5m+ 1).sinx +2m² + 2m = 0 có đúng 5 nghiệm thuộc khoảng 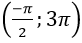. Tìm mệnh đề đúng?

A. m₀= - 2

B. m₀= 1

C. 

D.