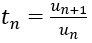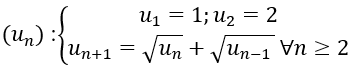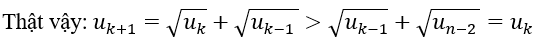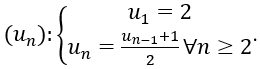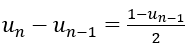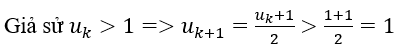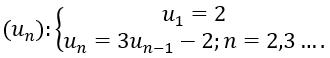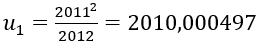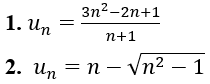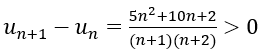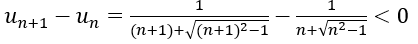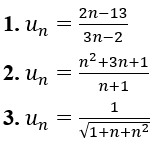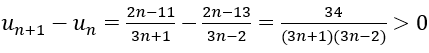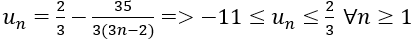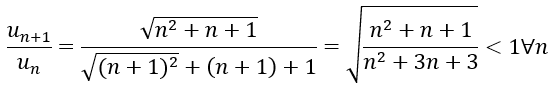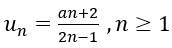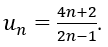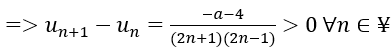Cách xét Tính đơn điệu, tính bị chặn của dãy số cực hay

A. Phương pháp giải & Ví dụ

1. Dãy số tăng, dãy số giảm

    ♦ Dãy số (u_n) gọi là dãy tăng nếu u_n < u_n+1 ∀n ∈ ¥

    ♦ Dãy số (u_n) gọi là dãy giảm nếu u_n > u_n+1 ∀n ∈ ¥

2. Dãy số bị chặn

    ♦ Dãy số (u_n) gọi là dãy bị chặn trên nếu có một số thực sao cho u_n < M ∀n ∈ ¥.

    ♦ Dãy số (u_n) gọi là dãy bị chặn dưới nếu có một số thực sao cho u_n > m∀n ∈ ¥..

    ♦ Dãy số vừa bị chặn trên vừa bị chặn dưới gọi là dãy bị chặn, tức là tồn tại số thực dương M sao cho |u_n | < M ∀n ∈ ¥..

    ♦ Để xét tính đơn điệu của dãy số (u_n) ta xét : k_n=(u_n+1-u_n)

        * Nếu k_n > 0∀n ∈ ¥ ⇒ dãy (u_n) tăng

        * Nếu k_n < 0∀n ∈ ¥ ⇒ dãy (u_n) giảm.

Khi u_n > 0 ∀n ∈ ¥ ta có thể xét 

        * Nếu t_n > 1 ⇒ dãy số (u_n) tăng

        * Nếu t_n < 1 ⇒ dãy số (u_n) giảm

    ♦ Để xét tính bị chặn của dãy số ta có thể dự đoán rồi chứng minh bằng quy nạp.

Ví dụ minh họa

Bài 1: Cho dãy số (u_n). Chứng minh rằng dãy (u_n) là dãy tăng và bị chặn

Đáp án và hướng dẫn giải

Ta chứng minh dãy (u_n) là dãy tăng bằng phương pháp quy nạp

* Dễ thấy: u₁ < u₂ < u₃.

* Giả sử u_k-1 < u_k ∀k ≥ 2, ta chứng minh u_k+1 > u_k.

Vậy (u_n) là dãy tăng.

Cũng bằng quy nạp ta chứng minh được u_n < 4 ∀n , hơn nữa u_n > 0

Nên dãy (u_n) là dãy bị chặn.

Bài 2: Cho dãy số (u_n). Chứng minh rằng dãy u_n là dãy giảm và bị chặn.

Đáp án và hướng dẫn giải

Do đó, để chứng minh dãy (u_n) giảm ta chứng minh u_n > 1∀n ≥ 1

Thật vậy:

Với n = 1 ⇒ u₁=2 > 1

Theo nguyên lí quy nạp ta có u_n > 1 ∀n ≥ 1

Suy ra u_n-u_n-1 < 0 ⇔ u_n < u_n-1 ∀n ≥ 2 hay dãy (u_n) giảm

Theo chứng minh trên, ta có: 1 < u_n < u₁=2∀n ≥ 1

Vậy dãy (u_n) là dãy bị chặn.

B. Bài tập vận dụng

Bài 1: Cho dãy số (u_n)

a) Viết 6 số hạng đầu của dãy

b) Chứng minh u_n=3^(n-1)+1;n=1,2…

Lời giải:

a) Ta có: u₁=2;u₂=4;u₃=10;u₄=28;u₅=82;u₆=244.

b) Chứng minh bài toán bằng phương pháp quy nạp hoặc chứng minh bằng cách sau

Ta có: u_n-1=3(u_(n-1)-1)=3² (u_(n-2)-1)=⋯=3^(n-1) (u₁-1)

Suy ra: u_n-1=3^(n-1) ⇒ u_n=1+3^(n-1).

Bài 2: Cho dãy số u_n=-5^(n-1)+3ⁿ+n+2;n=1,2…

a) Viết 5 số hạng đầu của dãy

b) Chứng minh rằng: u_n=2u_(n-1)+3^(n-1)-n.

Lời giải:

Với mọi n = 

Suy ra u_n < u₀-n+1=2012-n

Do đó: 2011 – n < u_n < 2012-n ⇒ [ u_n ]=2011-n

với n = 

Vì u₀=2011 và 

Nên [u₀ ]=2011-0,[u₁ ]=2011-1

Vậy [u_n ]=2011-n,n = .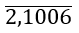

Bài 3: Xét tính tăng giảm của các dãy số sau

Lời giải:

1. Ta có:

nên dãy (u_n) là dãy tăng

2. Ta có:

Nên dãy (u_n) giảm.

Bài 4: Xét tính tăng, giảm và bị chặn của dãy số (u_n) , biết:

Lời giải:

1. Ta có:

với mọi n ≥ 1.

Suy ra u_(n+1) > u_n ∀n ≥ 1 ⇒ dãy (u_n) là dãy tăng.

Mặt khác:

Vậy dãy (u_n) là dãy bị chặn.

2. Ta có:

3. Ta có: u_n > 0 ∀n ≥ 1

⇒ u_(n+1) < u_n ∀n ≥ 1 ⇒ dãy (u_n) là dãy số giảm.

Mặt khác: 0 < u_n < 1 ⇒ dãy (u_n) là dãy bị chặn.

Bài 5: Cho dãy số (u_n):

a) Khi a = 4, hãy tìm 5 số hạng đầu của dãy

b) Tìm a để dãy số đã cho là dãy số tăng.

Lời giải:

a) Với a = 4 ta có:

Ta có: 5 số hạng đầu của dãy là

u₁=6; u₂=10/3; u₃=14/5; u₄=18/7; u₅=22/9.

b) Ta có dãy số u_n tăng khi và chỉ khi

⇒ -a-4 > 0 ⇒ a < -4