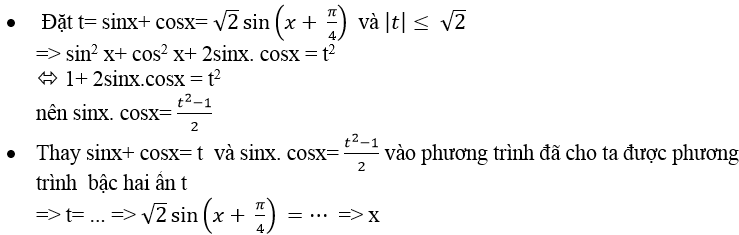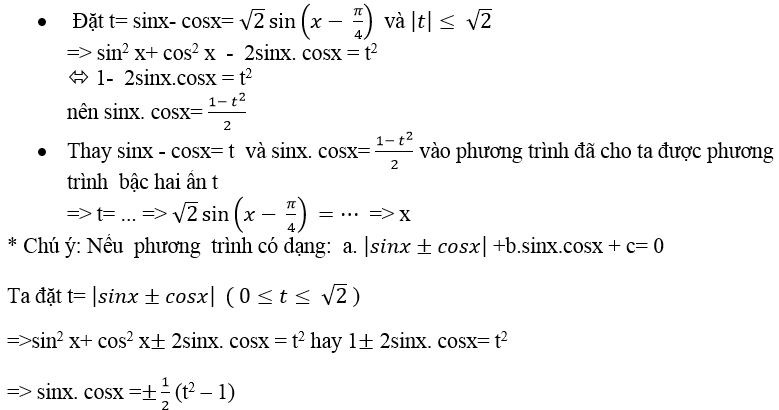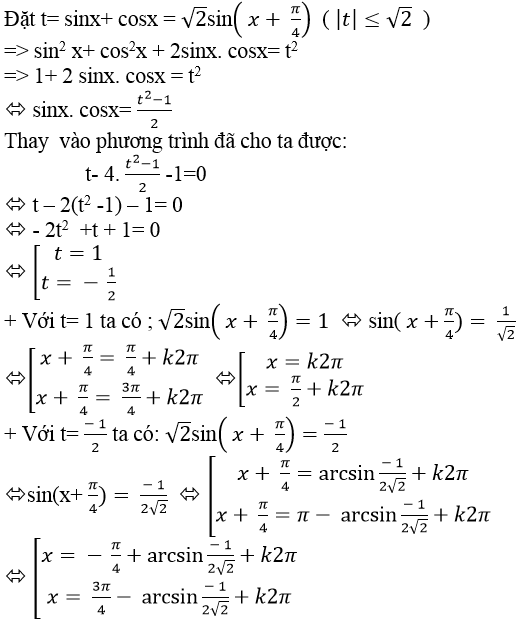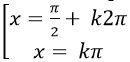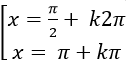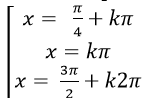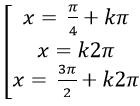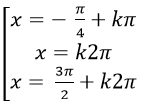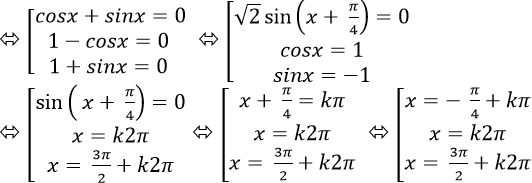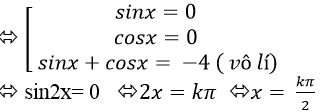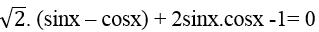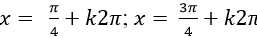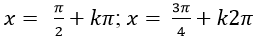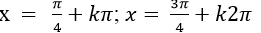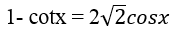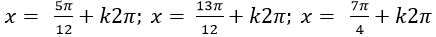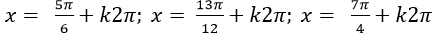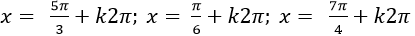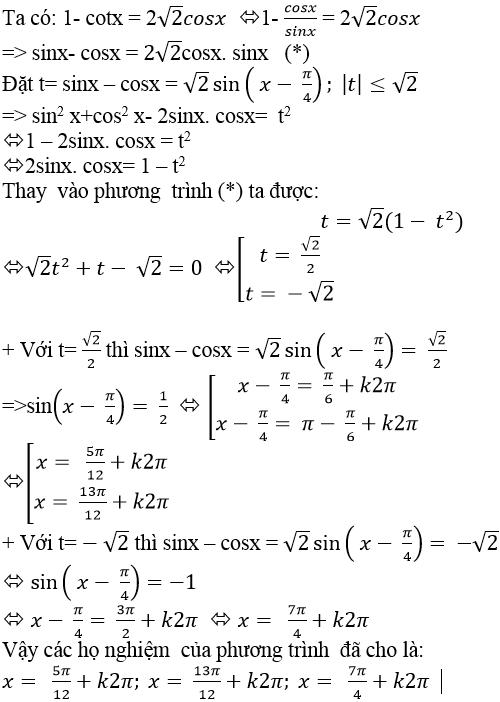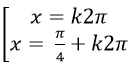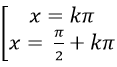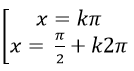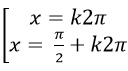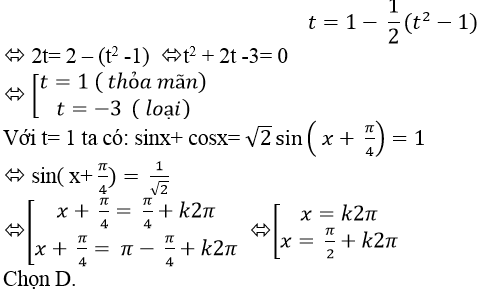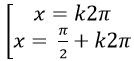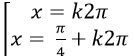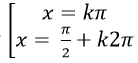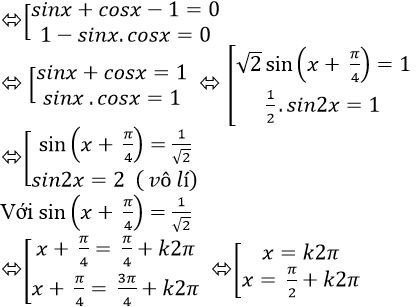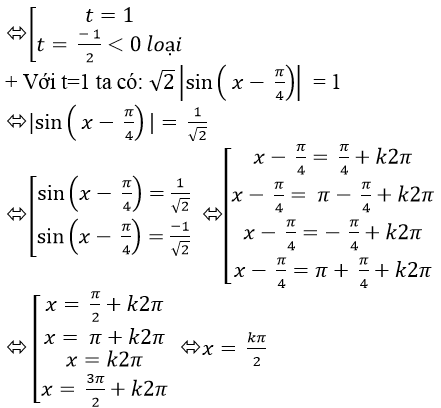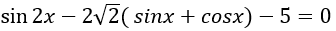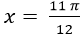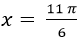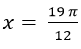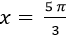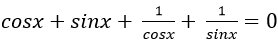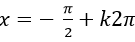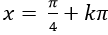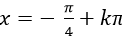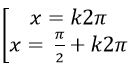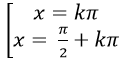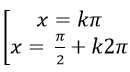Phương trình đối xứng, phản đối xứng đối với sinx và cosx

A. Phương pháp giải

+ Phương trình đối xứng đối với sinx và cosx có dạng:

a (sinx+ cosx)+ b.sinx. cosx + c = 0

Để giải phương trình này ta làm như sau:

+ Phương trình phản đối xứng đối với sinx và cosx có dạng:

a (sinx- cosx)+ b.sinx. cosx + c = 0

Để giải phương trình này ta làm như sau:

B. Ví dụ minh họa

Ví dụ 1: Phương trình sinx + cosx – 4.sinx.cosx – 1= 0 có bao nhiêu họ nghiệm

A. 2

B. 1

C. 3

D.4

Lòi giải

Ta có : sinx + cosx – 4sinx. cosx – 1= 0

Chọn D.

Ví dụ 2: Giải phương trình sin2x – 12(sinx - cosx) + 12 = 0

A.

B.

C.

D. Tất cả sai

Lời giải

Đặt t= sinx- cosx = √2 sin⁡( x- π/4) với |t| ≤ √2

⇒ sin² x + cos² x- 2sinx.cosx = t²

⇒ 1- sin2x = t² ⇒ sin2x= 1-t²

Thay vào phương trình đã cho ta được : 1- t2 -12. t+12=0

⇒ - t2 – 12t+ 13 = 0

Chọn C.

Ví dụ 3: Giải phương trình cos³ x + sin³ x= cos² x- sin²x

A.

B.

C.

D. Đáp án khác

Lời giải

Ta có: cos³ x + sin³ x= cos² x- sin²x

⇒ (cosx+ sinx) .(cos² x – cosx. sinx + sin² x)= (cosx- sinx) .(cosx +sinx)

⇒ (cosx+ sinx).( 1- cos x. sinx) – (cosx- sinx). (cosx+ sinx) = 0

⇒ (cosx+ sinx). ( 1- cosx. sinx – cosx+ sinx) = 0

⇒ (cosx+ sinx ).[ ( 1- cosx) + ( sinx- cosx. sinx) ]= 0

⇒ ( cosx + sinx) . [ ( 1- cosx) + sinx(1- cos) ]= 0

⇒ ( cosx+ sinx ).(1- cosx) . ( 1+ sinx) = 0

Chọn C.

Ví dụ 4: Giải phương trình sin³ x – cosx + cos³ x- sinx = 2sin2x

A. x= kπ

B. x= kπ/2

C. x= kπ/4

D. Đáp án khác

Lời giải

Ta có: sin³ x – cosx + cos³ x- sinx = 2sin2x

⇒ ( sin³ x+ cos³ x) - (cosx+ sinx) - 2sin2x= 0

⇒ ( sinx+ cosx) . (sin² x- sinx.cosx + cos² x) – ( cosx+ sinx) – 2sin2x = 0

⇒ ( sinx+ cosx) . (1- sinx. cosx) – (cosx + sinx) – 2.2.sinx. cosx=0

⇒ (sinx+ cosx).( 1- sinx.cosx- 1) – 4.sinx. cosx= 0

⇒ - (sinx+ cosx). sinx. cosx – 4.sinx.cosx=0 (*)

⇒ - sinx. cosx [ sinx+ cosx + 4] = 0

Chọn B.

Ví dụ 5: Giải phương trình 

A. 

B. 

C. 

D. Đáp án khác

Lời giải

Đặt t=sinx-cosx=√2sin⁡(x- π/4) với |t| ≤ √2

⇒ sin² x+ cos² x – 2sinx. cosx= t²

⇒ 1 – 2sinx. cosx = t²

⇒ 2sinx.cosx = 1- t²

Chọn C.

Ví dụ 6. Giải phương trình 

A.

B.

C.

D. Đáp án khác

Lời giải

+ Điều kiện: sinx ≠ 0

Chọn A.

Ví dụ 7. Phương trình: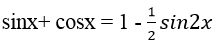 có nghiệm là:

A. 

B. 

C. 

D. 

Lời giải

Đặt sinx+cosx= t (|t| ≤ √2)

⇒ sin ² x+ cos² x+ 2sinx.cosx= t²

⇒ 1+ sin2x= t² ⇒ sin²x= t2 – 1

Thay vào phương trình đã cho ta được:

Chọn D.

Ví dụ 8. Phương trình 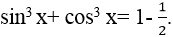 có nghiệm là:

A.

B.

C.

D.Đáp án khác

Lời giải

Ta có: sin³ x+ cos³ x= 1- 1/2. sin2x

⇒ ( sinx+ cosx) .( sin² x- sinx. cosx + cos² x) = 1- 1/2. 2sinx. cosx

⇒ (sinx+ cosx). ( 1- sinx. cosx) = 1- sinx. cosx

⇒ ( sinx+ cosx) . ( 1- sinx. cosx) –( 1 – sinx.cosx) = 0

⇒ (sinx+ cosx – 1) . ( 1 – sinx.cosx) = 0

Chọn A.

Ví dụ 9. Giải phương trình |sinx-cosx|+4.sinx.cosx-1=0

A. x= kπ/2

B. x= kπ

C. x= π/2+kπ

D. x= k2π

Lời giải

Đặt t= |sinx-cosx|= √2 |sin⁡( x- π/4) | (0 ≤ t ≤ √2)

⇒ sin² x+ cos² x – 2sinx. cosx = t²

⇒ 1 – 2sinx. cosx= t²

⇒ 2sinx. cosx= 1- t²

Khi đó; ta có: t+ 2(1-t² ) – 1= 0

⇒ - 2t² + t+ 1= 0

C. Bài tập vận dụng

Câu 1:Tìm nghiệm dương bé nhất của phương trình : 

A. x= 

B. x= 

C. x= 

D. x= 

Câu 2:Cho phương trình 5sin2x+sinx+cosx+6=0 . Trong các phương trình sau, phương trình nào tương đương với phương trình đã cho?

A. sin x = 1/2

B. cosx = 1

C.cot x= 1

D. 1+ sin2x=0

Câu 3:Câu 5.Giải phương trình: cos³ x+ sin³ x= cos2x

A. 

B. 

C. 

D. Đáp án khác

Câu 4:Giải phương trình; sin(x+ π/4)+sin2x+1=0

A.

B.

C.

D.

Câu 5:Giải phương trình 

A.

B.

C.

D.

Câu 6:Giải phương trình 

A. x=+kπ

B.

C.

D.

Câu 7:Cho phương trình sinx.cosx – sinx- cosx + m= 0 trong đó m là tham số thực. Để phương trình có nghiệm, các giá trị thích hợp của m là

A. -√2-1/2 ≤ m ≤ 1

B.√2-1/2 ≤ m ≤ 1

C.-√2-1/2 < m < 1

D. Đáp án khác

Câu 8:Phương trình 2sin2x-3√6 |sinx+cosx|+8=0 có nghiệm là

A.

B. 

C.

D. Đáp án khác

Câu 9:Giải phương trình sinx.cosx + 2(sinx+ cosx) = 2.

A.

B.

C.

D.