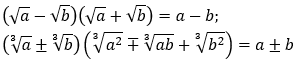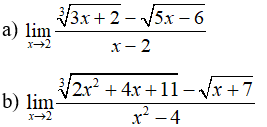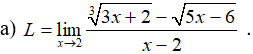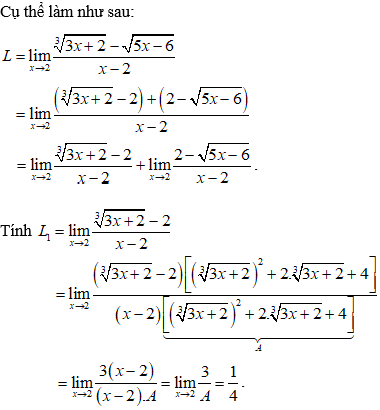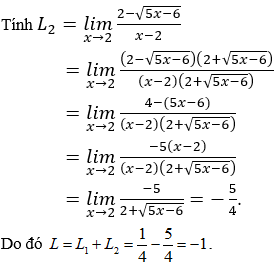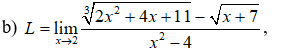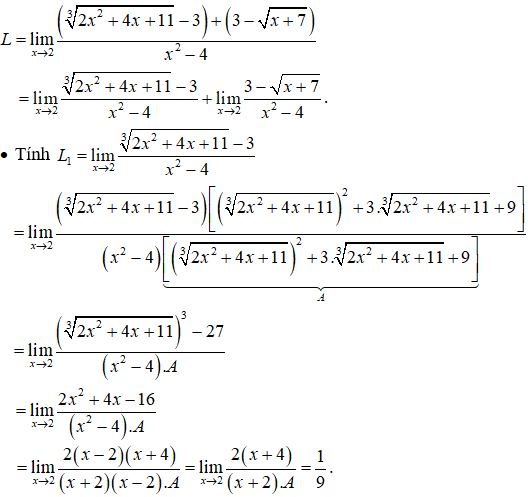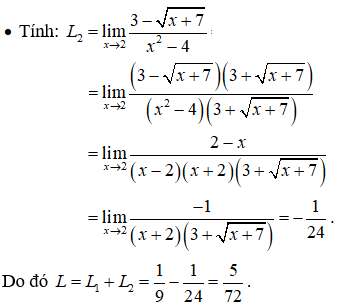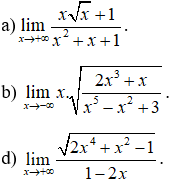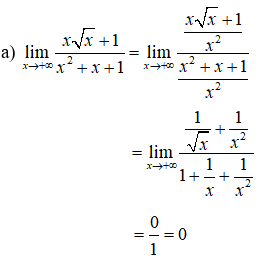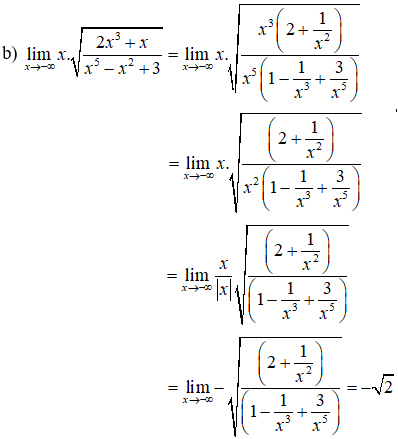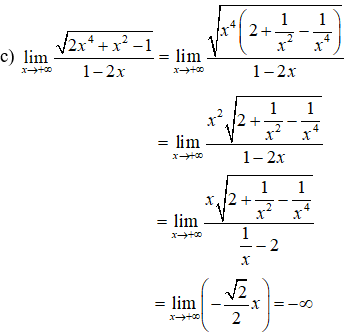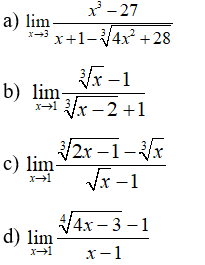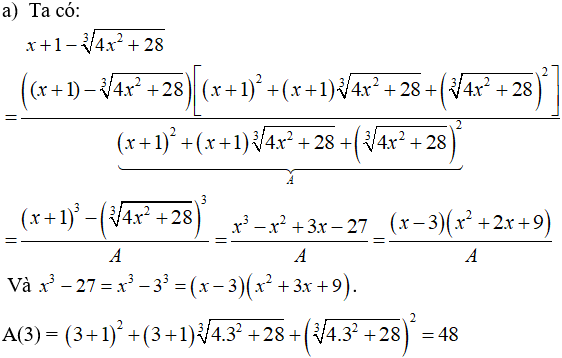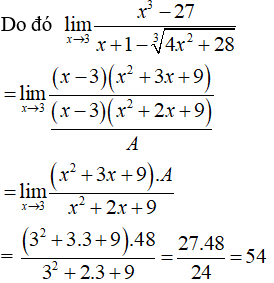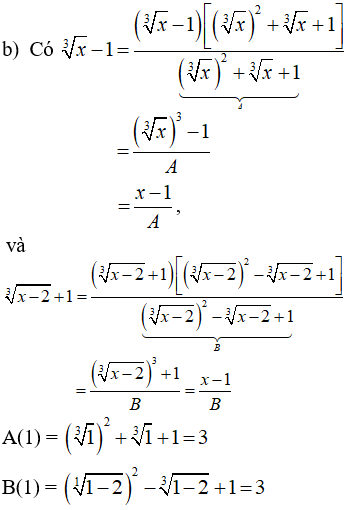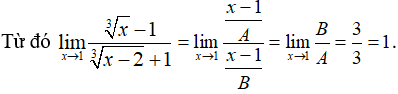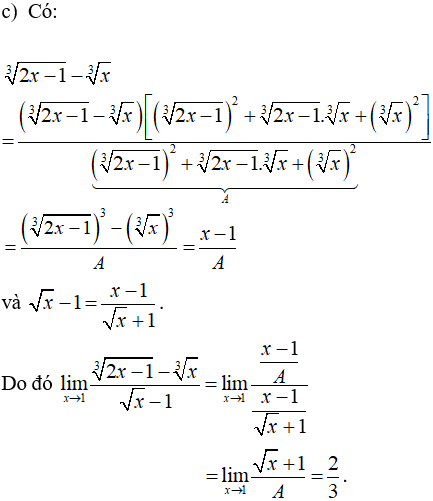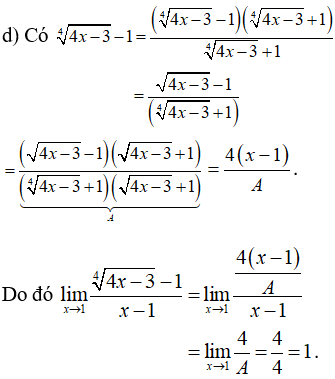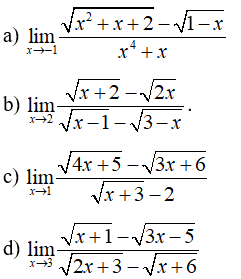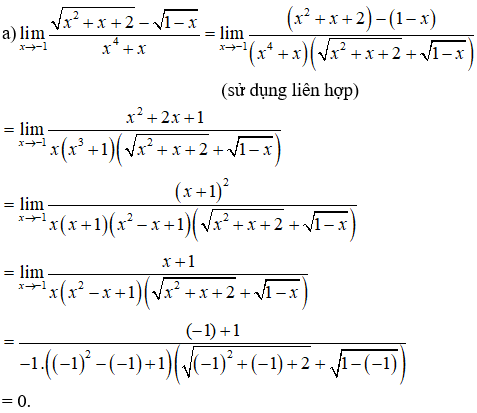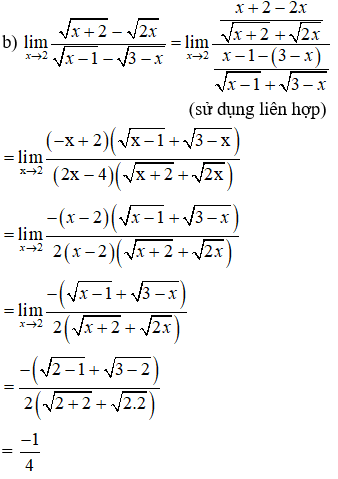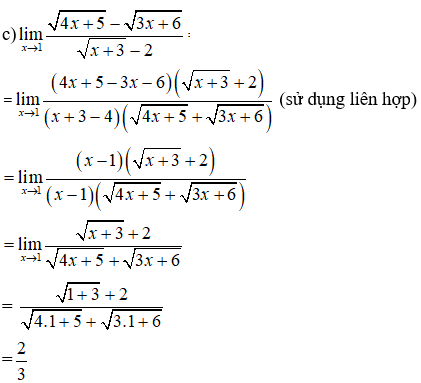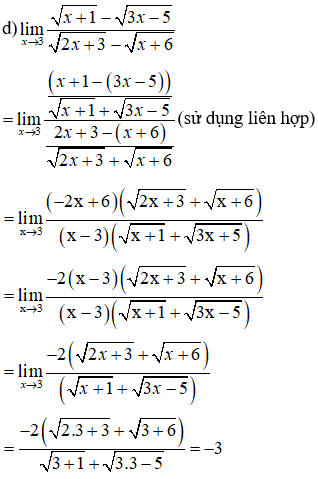Cách tính giới hạn của hàm số có chứa căn thức cực hay, chi tiết
Với Cách tính giới hạn của hàm số có chứa căn thức cực hay, chi tiết Toán học lớp 11 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách tính giới hạn của hàm số có chứa căn thức cực hay, chi tiết.
Cách tính giới hạn của hàm số có chứa căn thức cực hay, chi tiết
A. Phương pháp giải
- Đối với giới hạn hàm số dạng vô định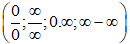 
, sử dụng các phép biến đổi liên hợp
- Đối với giới hạn hàm số tại vô cực, sử dụng phương pháp chia cả tử và mẫu cho lũy thừa bậc cao nhất của x.
B. Ví dụ minh họa
Ví dụ 1: Tìm các giới hạn sau:
Hướng dẫn giải:
Ta dễ dàng thấy đây là dạng vô định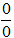 
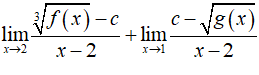
và tử số có hai căn thức khác loại, nên ta phải thêm bớt một hằng số c sao cho đưa được về dạng 
và mỗi giới hạn đều tính được giới hạn khi khử được dạng vô định bằng phương pháp nhân lượng liên hợp.
Kỹ thuật 1: Thay x = 2 vào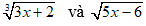 
đều bằng 2. Suy ra 2 là giá trị ta cần thêm bớt.
Kỹ thuật 2: Cho x – 2 = 0 ⇔ x = 2 sau đó giải hệ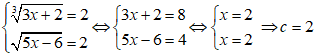 
là giá trị cần thêm bớt.
tương tự câu b) thay x = 2 vào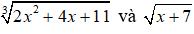 
đều bằng 3. Như vậy 3 là giá trị cần thêm và bớt, cụ thể:
Ví dụ 2: Tìm các giới hạn sau:
Hướng dẫn giải:
Ví dụ 3: Tìm các giới hạn sau:
Hướng dẫn giải:
Ví dụ 4: Tìm các giới hạn sau:
Hướng dẫn giải:
Bài viết liên quan
- Cách tìm giới hạn hàm số dạng 0 nhân vô cùng cực hay
- Tìm giới hạn hàm số dạng vô cùng trừ vô cùng, vô cùng trên vô cùng
- Cách tính giới hạn của hàm số có chứa trị tuyệt đối cực hay, chi tiết
- Cách tính giới hạn của hàm số lượng giác cực hay, chi tiết
- Cách chứng minh phương trình có nghiệm cực hay, chi tiết
