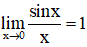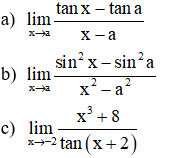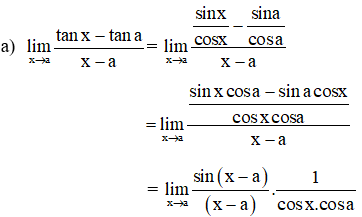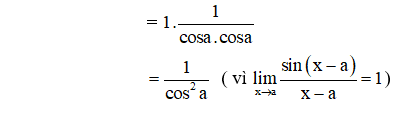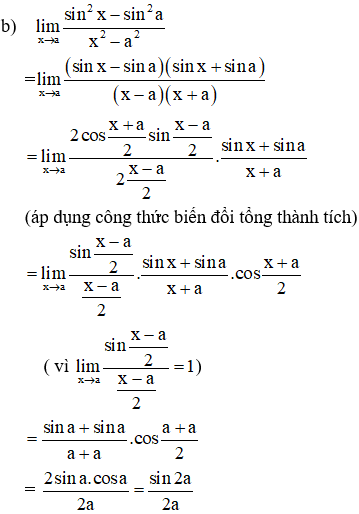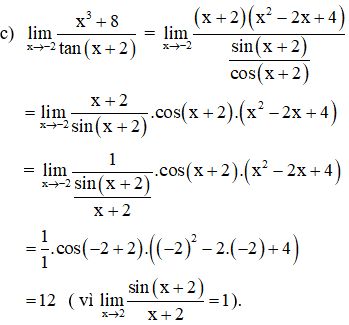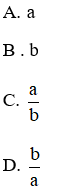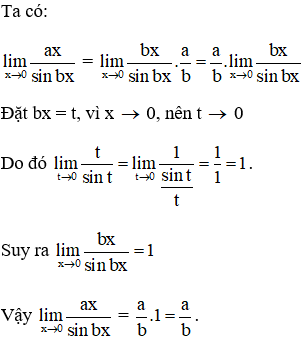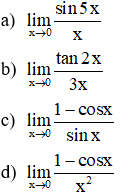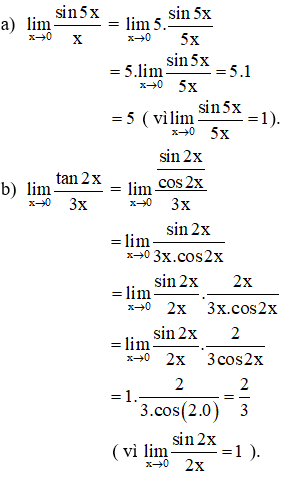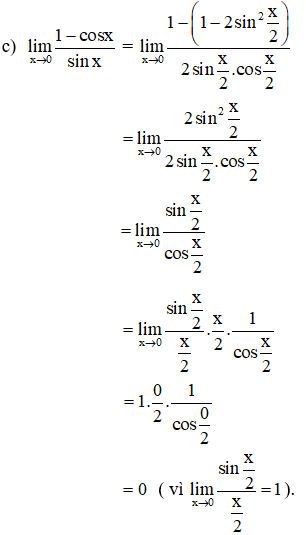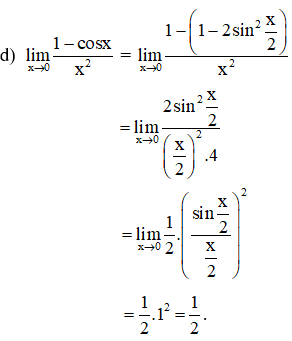Cách tính giới hạn của hàm số lượng giác cực hay, chi tiết
Với Cách tính giới hạn của hàm số lượng giác cực hay, chi tiết Toán học lớp 11 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách tính giới hạn của hàm số lượng giác cực hay, chi tiết.
Cách tính giới hạn của hàm số lượng giác cực hay, chi tiết
A. Phương pháp giải
- Áp dụng giới hạn đặc biệt: 
- Các bước tìm giới hạn hàm số lượng giác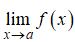 
với f(x) là hàm số lượng giác
● Bước 1: Sử dụng các công thức lượng giác cơ bản, công thức nhân đôi, công thức cộng, công thức biến đổi,… (đã được học ở chương 6 Đại số 10) để biến đổi hàm số lượng giác f(x) về cùng dạng giới hạn đặc biệt nêu trên.
● Bước 2: Áp dụng các định lý về giới hạn để tìm giới hạn đã cho.
B. Ví dụ minh họa
Ví dụ 1: Tính các giới hạn sau (với a là số thực khác 0)
Hướng dẫn giải:
(áp dụng công thức cộng: sin(a-b) = sina.cosb-cosa.sinb)
Ví dụ 2: Cho a và b là hai số thực khác 0. Khi đó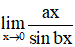 
bằng:
Hướng dẫn giải:
Đáp án C
Ví dụ 3: Tính các giới hạn sau:
Hướng dẫn giải:
