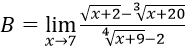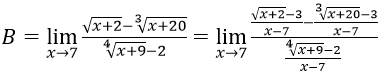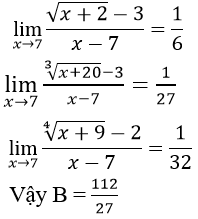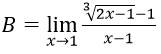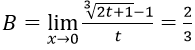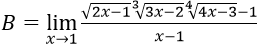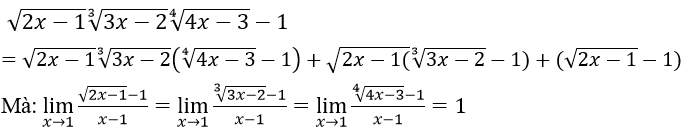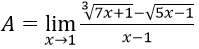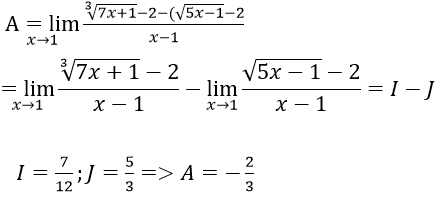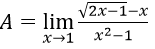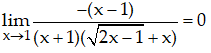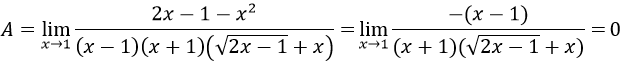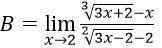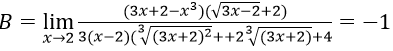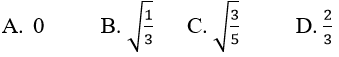Cách tìm giới hạn hàm số dạng 0/0, dạng vô cùng trên vô cùng cực hay
Với Cách tìm giới hạn hàm số dạng 0/0, dạng vô cùng trên vô cùng cực hay Toán học lớp 11 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Cách tìm giới hạn hàm số dạng 0/0, dạng vô cùng trên vô cùng cực hay.
Cách tìm giới hạn hàm số dạng 0/0, dạng vô cùng trên vô cùng cực hay
A. Phương pháp giải & Ví dụ
Tìm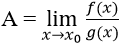 
trong đó f(x0) = g(x0) = 0
Dạng này ta gọi là dạng vô định 0/0
Để khử dạng vô định này ta sử dụng định lí Bơzu cho đa thức:
Định lí: Nếu đa thức f(x) có nghiệm x = x0 thì ta có :f(x) = (x-x0)f1(x)
* Nếu f(x) và g(x) là các đa thức thì ta phân tích
f(x) = (x-x0)f1(x)và : g(x) = (x-x0)g1(x).
Khi đó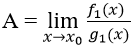 
, nếu giới hạn này có dạng 0/0 thì ta tiếp tục quá trình như trên.
Ví dụ minh họa
Bài 1: 
Hướng dẫn:
Ta có:
Mà
Bài 2: 
Hướng dẫn:
Đặt t = x - 1 ta có:
Bài 3: 
Hướng dẫn:
Ta có:
Nên ta có B = 1 + 1 + 1 = 3
Bài 4: 
Hướng dẫn:
Ta có:
Vậy A = -2/3
Bài 5: Tìm các giới hạn sau: 
Hướng dẫn:
Ta có: 
Bài 6: Tìm giới hạn sau: 
Hướng dẫn:
Ta có:
B. Bài tập vận dụng
Bài 1: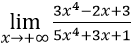 
bằng:
A. 0 B. 4/9 C. 3/5 D. +∞
Bài 2: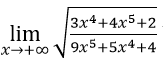 
bằng:
Bài 3: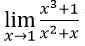 
bằng:
A. -3
B. -1
C. 0
D. 1
Bài 4: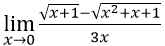 
bằng:
A. 0 B. -1/6 C. -1/2 D. -∞
Bài 5: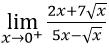 
bằng:
A. +∞ B. 2/5 C. -7 D. -∞
Bài 6: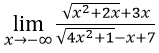 
bằng:
A. 2/3 B. 1/2 C. -2/3 D. -1/2
Bài 7: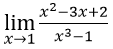 
bằng:
A. -2/3 B. -1/3 C. 0 D. 1/3
Bài 8: 
bằng:
A. +∞
B. 4
C. 0
D. -∞
Bài 9: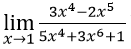 
bằng số nào sau đây?
Bài 10: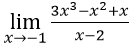 
bằng
A. 5 B. 1 C. 5/3 D. -5/3
Bài 11: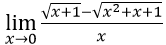 
bằng:
A. 0 B. -1 C. -1/2 D. -∞
Bài 12: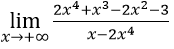 
bằng:
A. -2
B. -1
C. 1
D. 2
Bài 13: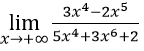 
bằng:
A. -∞ B. 3/5 C. -2/5 D. 0
Bài 14: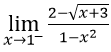 
bằng:
A. 1/4 B. 1/6 C. 1/8 D. -1/8
Bài 15: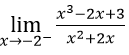 
bằng:
A. +∞ B. 1/8 C. -9/8 D. -∞
