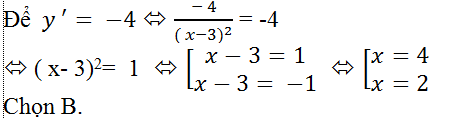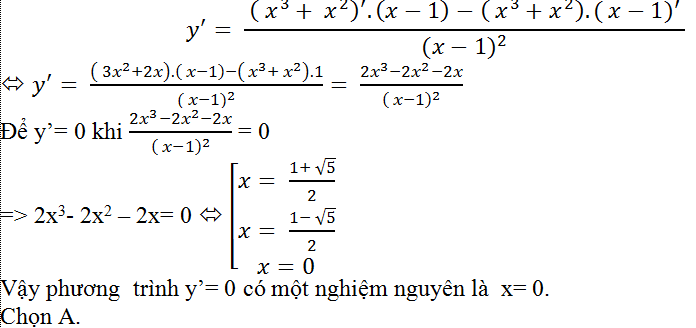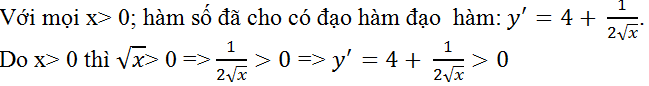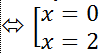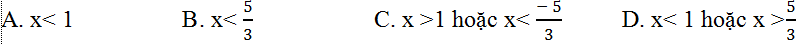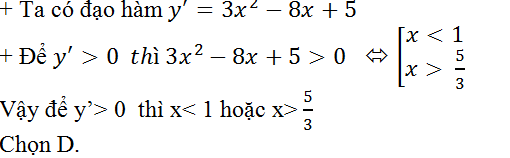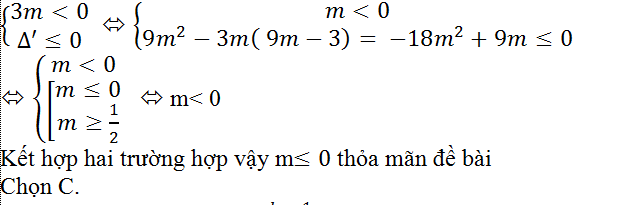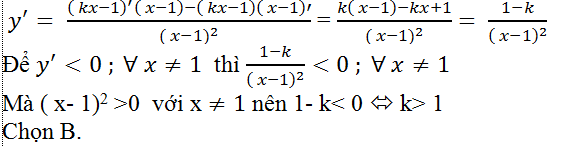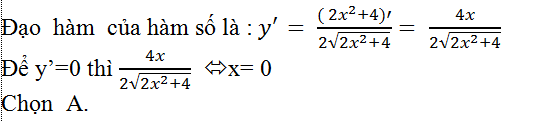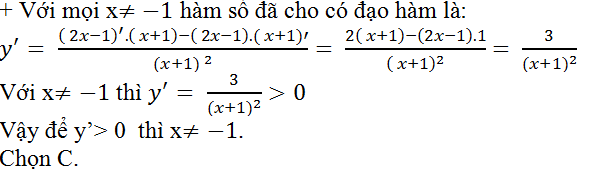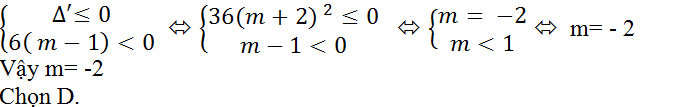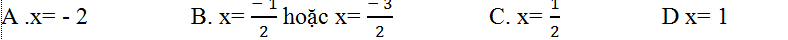Ứng dụng đạo hàm để giải phương trình, bất phương trình cực hay

A. Phương pháp giải

+ Bước 1: Tính đạo hàm của hàm số.

+ Bước 2: Lập phương trình; bất phương trình.

+ Bước 3: Giải phương trình; bất phương trình.

B. Ví dụ minh họa

Ví dụ 1. Cho hàm số y= (2x-2)/(x-3). Giải phương trình y'= -4.

A .x= - 2         B. x= 4 hoặc x= 2         C. x= 2         D x= - 3

Hướng dẫn giải

Hàm số đã cho xác định với mọi x≠3.

Đạo hàm của hàm số đã cho với x≠3 là :

Ví dụ 2. Cho hàm số y= (x³+ x²)/(x-1). Phương trình y'=0 có mấy nghiệm nguyên?

A. 1         B. 0         C. 2         D. 3

Hướng dẫn giải

+ Hàm số đã cho có đạo hàm tại mọi điểm x≠1. Khi đó; đạo hàm của hàm số là:

Ví dụ 3. Cho hàm số y= 2mx – mx³. Với những giá trị nào của m để x= -1 là nghiệm của bất phương trình y'<1?

A. m > - 1         B. m < 1         C.m= 1         D. m < - 1

Hướng dẫn giải

Ta có đạo hàm: y’= 2m- 3mx²

Bất phương trình y' <1 khi 2m-3mx² <1

Do x= -1 là nghiệm của bât phương trình nên ta có: 2m- 3m.(-1)² < 1

⇔ - m < <1 hay m >- 1.

Chọn A.

Ví dụ 4. Cho hàm số y= x⁴+ 2x³ – k.x²+ x- 10. Tìm k để phương trình y'=1 có một nghiệm là x= 1?

A. k= 5         B. k= -5         C. k= 2         D. k= - 3

Hướng dẫn giải

+ Ta có đạo hàm: y'= 4x³+ 6x² - 2kx+ 1.

+ Để y’= 1 thì 4x³+ 6x² - 2kx+ 1 = 1

⇔ 4x³+ 6x² – 2kx = 0. (*)

Do phương trình y’= 1 có một nghiệm là x= 1 nên phương trình (*) có một nghiệm x= 1. Suy ra: 4.13 + 6.12 – 2.k.1= 0 ⇔ 10- 2k = 0

⇔ k= 5.

Chọn A.

Ví dụ 5. Cho hàm số y= 4x+√x-10. Nghiệm của phương trình y'=0 là

A.x=1         B. x= 4         C. x= 9         D. Vô nghiệm

Hướng dẫn giải

⇒ Phương trình y’= 0 vô nghiệm.

Chọn D.

Ví dụ 6. Cho hàm số y= 2x³ – 6x²+ 2000. Phương trình y'= 0 có mấy nghiệm?

A. 0         B. 1         C. 2         D. 3

Hướng dẫn giải

+ Ta có đạo hàm: y'=6x²-12x

+ Để y'=0 thì 6x²-12x=0

Vậy phương trình y’= 0 có hai nghiệm.

Chọn C.

Ví dụ 7. Cho hàm số y= x³-4x²+5x-9. Với giá trị nào của x thì y'>0?

Hướng dẫn giải

Ví dụ 8.Tìm m để các hàm số y= mx³- 3mx² + (9m- 3) x+ 3 có y' ≤0 ; ∀x∈R.

A. m< 1         B. m< 0         C. m ≤0         D. m > 0

Hướng dẫn giải

Hàm số đã cho xác định với mọi x.

Đạo hàm của hàm số là: y' = 3mx² – 6mx + 9m-3

Để y' ≤0 ; ∀x∈R thì 3mx² – 6mx + 9m - 3 ≤0 ; ∀x∈R (*)

+ Nếu m= 0 thì (*) trở thành: - 3≤0 (luôn đúng với mọi x)

⇒ m= 0 thỏa mãn.

+ Nếu m≠0 thì để (*) luôn đúng với mọi x khi và chỉ khi:

Ví dụ 9. Cho hàm số y= (kx-1)/(x-1). Xác định các giá trị của k để y'<0 ; ∀ x≠1

A. k <- 1         B. k> 1         C. k< - 2         D.k > 3

Hướng dẫn giải

Hàm số đã cho có đạo hàm với mọi x≠1.

Với mọi x≠1 hàm số có đạo hàm là:

Ví dụ 10. Cho hàm số y= √(2x²+4). Với những giá trị nào của x thì y'=0?

A. x= 0         B. x= 1         C. x= 2         D. không có giá trị nào thỏa mãn

Hướng dẫn giải

Hàm số đã cho xác định với mọi x.

Ví dụ 11. Cho hàm số y= (2x-1)/(x+1). Với những giá trị nào của x thì y’ >0

A. R.         B. x> 0         C.R\{-1}         D. -1

Hướng dẫn giải

Ví dụ 12. Cho hàm số y= 2( m-1)x³- 6(m+ 2)x²+ 2 tìm m để y' ≥0 ; ∀ x∈R?

A. m < - 2         B. m>2         C. m > -2         D. m= -2

Hướng dẫn giải

+ Hàm số xác định với mọi x∈R.

+ Đạo hàm của hàm số: y'=6(m-1) x²-12( m+2).x

+ Để y' ≥0 ; ∀ x∈R khi và chỉ khi :

6(m-1) x²-12( m+2).x ≥0 đúng ∀ x∈R ( *)

+ Với m= 1 thì (*)trở thành: -36 x ≥0 ⇔ x ≥0 ( loại)

+ Với m≠1 thì để (*) đúng với mọi x thì:

C. Bài tập vận dụng

Câu 1: Tìm m để các hàm số y= mx³- ( m- 2)x² + ( m+ 1) x+ 7 có y' ≤0 ; ∀x∈R.

A. m< 4         B. m> - 2         C. m ≤4         D. m ≤-4

Câu 2: Cho hàm số y= (2x+k)/(4x-1). Xác định các giá trị của k để y'<0 ; ∀ x≠1/4

Câu 3: Cho hàm số y= √(x²+4x+19). Xác định các giá trị của x là nghiệm của bất phương trình y’<0 ?

A. x< -2         B. x> 4         C. x< 1         D. x>2

Câu 4: Cho hàm số y=(3x+1)/(2x+2). Giải phương trình y'= 4.

Câu 5: Cho hàm số y= (2 x²-2x)/(x+1). Phương trình y'=0 có nghiệm là?

A. x= -1 hoặc x= 0         B. x= 0         C. x= 1 hoặc x= -1         D. x= 2 hoặc x= - 1

Câu 6: Cho hàm số y= x³ – mx² + 3x+ 3. Với những giá trị nào của m để x= 6 là nghiệm của bất phương trình y'<3?

A. m > 6         B. m > 9         C.m < - 6         D. m < 9

Câu 7: Cho hàm số y= ( m+1)x³- 3(2m- 1)x²+ x tìm m để y' ≤0 ; ∀ x∈R?

A. m < - 2         B. m>2         C. m > -2         D. Không có giá trị nào

Câu 8: Cho hàm số y= x³ – x²+ 2000x+ 8. Phương trình y'= 0 có mấy nghiệm?

A. 0         B. 1         C. 2         D. 3

Câu 9: Cho hàm số y= 2x³-4x²+2x-9. Với giá trị nào của x thì y'<0?

A. x< 1         B. x< 1/3         C. x >1 hoặc x< 1/3         D. 1/3< x <1

Câu 10: Cho hàm số y= x⁴ -3x³ +2k.x²+ 4x - 6. Tìm k để phương trình y'=1 có một nghiệm là x= 1?

A. k= 1/2         B. k= 2/3         C. k= 2         D. k= - 3

Câu 11: Cho hàm số y= x²-32√x+8. Nghiệm của phương trình y'=0 là

A.x=1         B. x= 4         C. x= 9         D. Vô nghiệm

Câu 12: Cho hàm số y= (x+2)/(x-3). Với những giá trị nào của x thì y’ >0

A. R.         B. x > 0         C.R\{ 3}         D. Không có giá trị nào