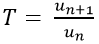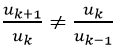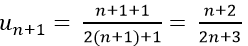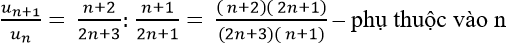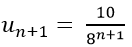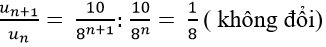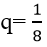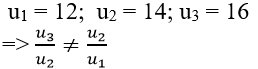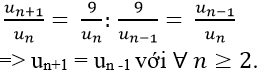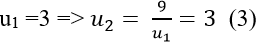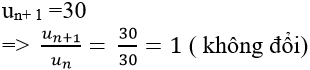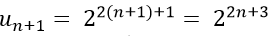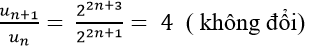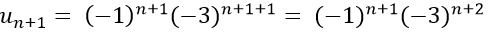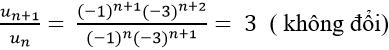Cách chứng minh một dãy số là cấp số nhân cực hay có lời giải

A. Phương pháp giải

Cách 1. Chứng minh ∀n ≥ 1; u_n+1 = u_n q trong đó q là một số không đổi.

Cách 2. Nếu u_n ≠ 0 với mọi n thì ta lập tỉ số 

T là hằng số thì (u_n) là cấp số nhân có công bội q = T.

T phụ thuộc vào n thì (u_n) không là cấp số nhân.

Cách 3. Chỉ ra tồn tại số k ≥ 2 sao cho: 

B. Ví dụ minh họa

Ví dụ 1: Cho dãy số (u_n) xác định bởi 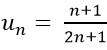. Chứng minh dãy số (u_n) không phải là cấp số nhân

Hướng dẫn giải:

Ta có 

Xét tỉ số: 

=> Dãy số (u_n) không là cấp số nhân.

Ví dụ 2: Cho dãy số (u_n) xác định bởi 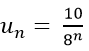. Chứng minh dãy số (u_n) là cấp số nhân.

Hướng dẫn giải:

Ta có: 

Xét tỉ số: 

=> dãy số (u_n) là cấp số nhân với 

Ví dụ 3: Cho dãy số (u_n) xác định bởi u_n = 2n+ 10. Chứng minh dãy số (u_n) không là cấp số nhân.

Hướng dẫn giải:

Ta có:

=> dãy số (u_n) không là cấp số nhân.

Ví dụ 4: Cho dãy số (u_n) xác định bởi 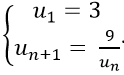. Chứng minh rằng dãy số (u_n) là cấp số nhân?

Hướng dẫn giải:

* Ta có:

* Do đó có: u₁ = u₃ = u₅ =...= u_{2n+ 1} = ... (1)

Và u₂ = u₄ = u₆ = ...= u_2n = ... (2)

Theo đề bài có 

Từ (1), (2) ,(3) suy ra u₁= u₂ = u₃ =...= u_2n = u_{2n+ 1} =....

Kết luận (u_n) là cấp số nhân với công bội q = 1.

Ví dụ 5: Cho dãy số (u_n) được xác định bởi u_n = 30. Chứng minh rằng ( u_n) là cấp số nhân.

Hướng dẫn giải:

Ta có:

=> (u_n) là cấp số nhân với q = 1.

Ví dụ 6: Cho dãy số (u_n) xác định bởi: u_n= 2²ⁿ⁺¹. Chứng minh (u_n) là cấp số nhân

Hướng dẫn giải:

Ta có: 

Xét tỉ số 

=> Dãy số (u_n) là cấp số nhân với công bội q = 4.

Ví dụ 7: Cho dãy số (u_n) xác định bởi: u_n = (-1)ⁿ.(-3)ⁿ⁺¹. Chứng minh (u_n) là cấp số nhân.

Hướng dẫn giải:

Ta có: 

Xét tỉ số 

=> Dãy số (u_n) là cấp số nhân với công bội q = 3.

C. Bài tập vận dụng

Câu 1: Cho dãy số (u_n) xác định bởi: u_n = 10n + 10. Chứng minh dãy số (u_n) không là cấp số nhân.

Câu 2: Cho dãy số (u_n): 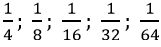. Chứng minh dãy số (u_n) là cấp số nhân.

Câu 3: Cho dãy số (u_n) xác định bởi: 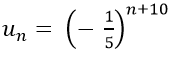. Chứng minh dãy số (u_n) là cấp số nhân.

Câu 4: Cho dãy số (u_n) được xác định bởi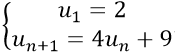. Đặt vn= u_n + 3. Chứng minh (vn) là cấp số nhân.

Câu 5: Cho dãy số (u_n) xác định bởi 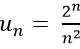. Chứng minhh rằng dãy số (u_n) không là cấp số nhân.

Câu 6: Cho dãy số (u_n) xác định bởi 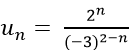. Chứng minh (u_n) là cấp số nhân.

Câu 7: Cho dãy số (u_n) xác định bởi : u_n= n. 2n. Chứng minh dãy số (u_n) không là cấp số nhân.