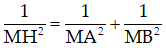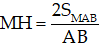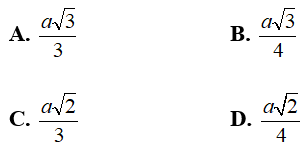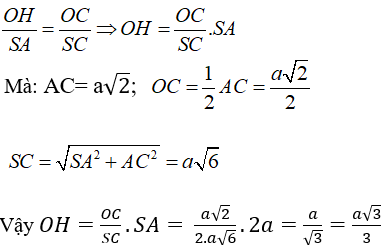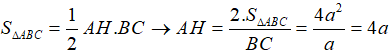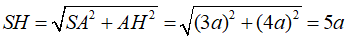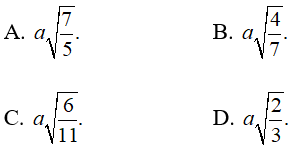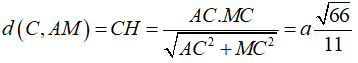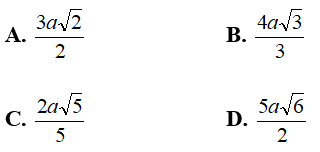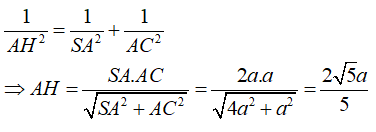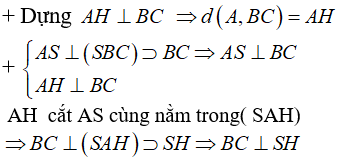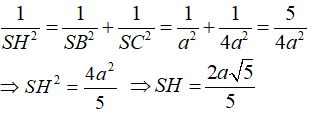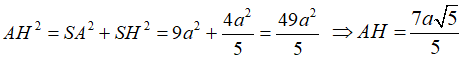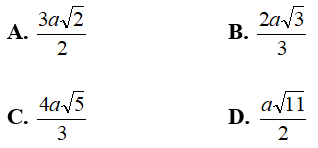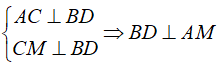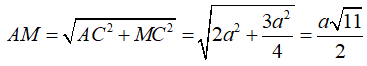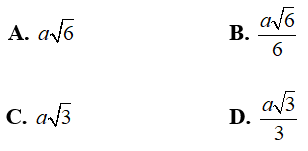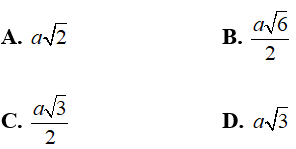Cách tính khoảng cách từ một điểm đến một đường thẳng cực hay

A. Phương pháp giải

- Để tính khoảng cách từ điểm M đến đường thẳng Δ ta cần xác định được hình chiếu H của điểm M trên đường thẳng Δ. Khi đó MH chính là khoảng cách từ M đến đường thẳng. Điểm H thường được dựng theo hai cách sau:

   + Trong mp(M; Δ) vẽ MH vuông góc Δ ⇒ d(M; Δ) = MH

   + Dựng mặt phẳng (α) qua M và vuông góc với Δ tại H ⇒ d(M; Δ) = MH.

- Hai công thức sau thường được dùng để tính MH:

   + Tam giác AMB vuông tại M và có đường cao AH thì 

   + MH là đường cao của tam giác MAB thì 

B. Ví dụ minh họa

Ví dụ 1: Cho hình chóp S. ABCD có SA ⊥ (ABCD) ; SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.

Hướng dẫn giải

Chọn A

+ Kẻ OH ⊥ SC , khi đó d(O; SC) = OH

+ Ta có: ΔSAC ∼ ΔOHC (g.g) (g-g) nên

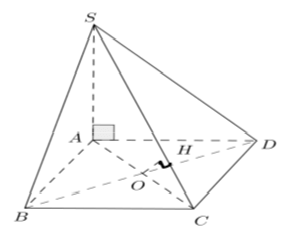
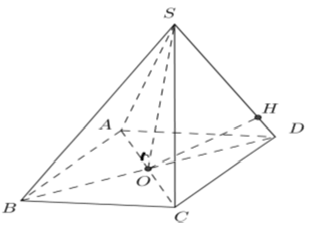
Ví dụ 2: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng α. Khoảng cách từ tâm của đáy đến một cạnh bên bằng

Hướng dẫn giải

Chọn D

+ Gọi O là tâm của hình vuông ABCD.

+ Do S.ABCD là hình chóp tứ giác đều nên SO ⊥ (ABCD)

+ Theo giả thiết góc giữa cạnh bên và mặt đáy là α nên : ∠SDO = α

Kẻ OH ⊥ SD, khi đó d(O, SD) = OH

Ta có: BD = a√a nên OD = (1/2)BD = (1/2).a√2 = (a√2)/2

+ Xét tam giác vuông OHD:

OH = OD.sinα = (a√2/2).sinα

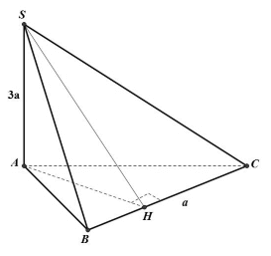
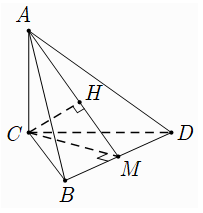
Ví dụ 3: Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA = 3a. Diện tích tam giác ABC bằng 2a²; BC = a. Khoảng cách từ S đến BC bằng bao nhiêu?

A. 2a               B. 4a               C.3a               D. 5a

Hướng dẫn giải

+ Kẻ AH vuông góc với BC

Ta có: SA ⊥ (ABC) ⇒ SA ⊥ BC

Lại có: AH ⊥ BC nên BC ⊥ (SAH)

⇒ SH ⊥ BC và khoảng cách từ S đến BC chính là SH

+ Ta có tam giác vuông SAH vuông tại A nên ta có

Chọn D

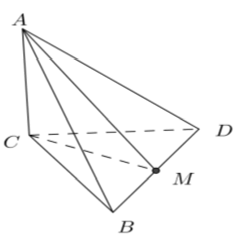
Ví dụ 4: Cho hình chóp ABCD có cạnh AC ⊥ (BCD) và BCD là tam giác đều cạnh bằng a. Biết AC = a√2 và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng

Hướng dẫn giải

+ Do tam giác BCD đều cạnh a nên đường trung tuyến CM đồng thời là đường cao và MC = a√3/2

+ Ta có: AC ⊥ (BCD) ⇒ AC ⊥ CM

Gọi H là chân đường vuông góc kẻ từ C đến AM

Ta có: 

Chọn đáp án C

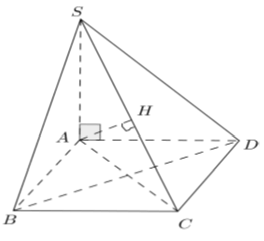
Ví dụ 5: Cho hình chóp S.ABCD có SA ⊥ (ABCD) , đáy ABCD là hình thoi cạnh bằng a và ∠B = 60° . Biết SA = 2a. Tính khoảng cách từ A đến SC.

Hướng dẫn giải

Chọn C

Kẻ AH ⊥ SC, khi đó d(A; SC) = AH

+ Do ABCD là hình thoi cạnh bằng a và ∠B = 60° nên tam giác ABC đều ⇒ AC = a

+ Do SA vuông góc (ABCD) nên SA vuông góc AC hay tam giác SAC vuông tại A.

Trong tam giác vuông ta có:

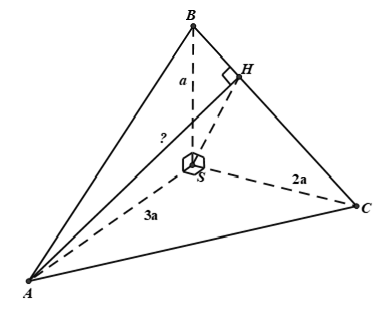
Ví dụ 6: Cho tứ diện SABC trong đó SA; SB; SC vuông góc với nhau từng đôi một và SA = 3a; SB = a; SC = 2a. Khoảng cách từ A đến đường thẳng BC bằng:

Hướng dẫn giải

Chọn đáp án B

Xét trong tam giác SBC vuông tại S có SH là đường cao ta có:

+ Ta dễ chứng minh được AB ⊥ (SBC) ⊃ SH ⇒ AS ⊥ SH

⇒ tam giác SAH vuông tại S.

Áp dụng định lsi Pytago trong tam giác ASH vuông tại S ta có:

Chọn B

Ví dụ 7: Cho hình chóp A.BCD có cạnh AC ⊥ (BCD) và BCD là tam giác đều cạnh bằng a . Biết AC = a√2 và M là trung điểm của BD . Khoảng cách từ A đến đường thẳng BD bằng:

Hướng dẫn giải

Chọn D

Ta có: 

(Định lý 3 đường vuông góc)

⇒ d(A, BD) = AM, CM = a√3/2 (vì tam giác BCD đều).

+ AC vuông góc ( BCD) nên AC vuông góc CM hay tam giác ACM vuông tại C.

⇒ 

C. Bài tập vận dụng

Câu 1: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ ba điểm nào sau đây đến đường chéo AC’ bằng nhau ?

A. A’, B, C’               B. B, C, D               C. B’, C’, D’               D. A, A’, D’

Câu 2: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SO = a√3/3. Khoảng cách từ điểm O đến cạnh bên SA bằng

Câu 3: Cho hình chóp S.ABC trong đó SA; AB; BC vuông góc với nhau từng đôi một. Biết SA = 3a, AB = a√3, BC = a√6. Khoảng cách từ B đến SC bằng

A. a√2               B. 2a              C. 2a√3              D. a√3

Câu 4: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD’ bằng

Câu 5: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD’ bằng

Câu 6: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng DB’ bằng