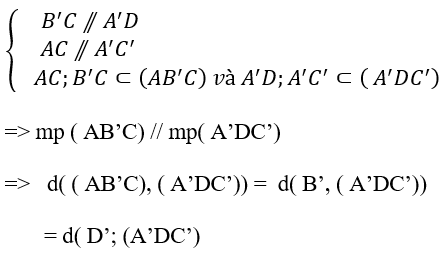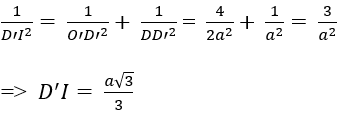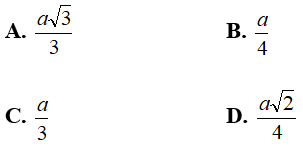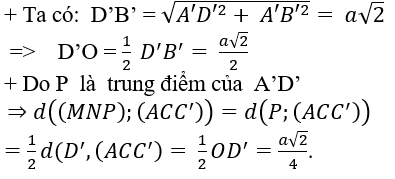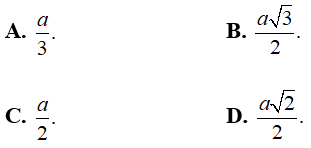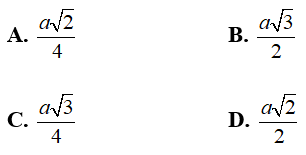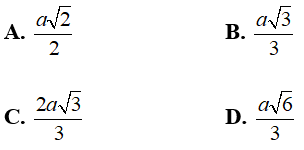Cách tính khoảng cách giữa hai mặt phẳng song song cực hay

A. Phương pháp giải

Cho hai mặt phẳng (P) và (Q) song song với nhau. Để tính khoảng cách giữa (P) và (Q) ta thực hiện các bước:

   + Bước 1: Chọn một điểm A trên (P) sao cho khoảng cách từ A đến (Q) có thể được xác định dễ nhất.

   + Bước 2: Kết luận: d((P); (Q)) = d(A; (Q)).

B. Ví dụ minh họa

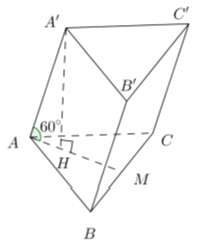
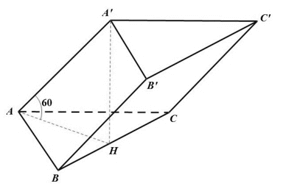
Ví dụ 1: Cho hình lăng trụ tam giác ABC.A’B’C’ có các cạnh bên hợp với đáy những góc bằng 60°, đáy ABC là tam giác đều và A’ cách đều A, B; C. Tính khoảng cách giữa hai đáy của hình lăng trụ.

Hướng dẫn giải

Chọn A

+ Vì tam giác ABC đều và AA’ = BA’ = CA’ (giả thiết) nên A’.ABC là hình chóp đều.

Gọi A’H là chiều cao của lăng trụ, suy ra H là trọng tâm tam giác ABC

Lăng trụ ABC.A’B’C’ có các cạnh bên hợp với đáy góc 60° nên ∠A'AH = 60°.

+ Xét tam giác AHA’ có: A'H = AH.tan60° = ((a√3)/3).√3 = a

+ lại có; (ABC) // (A’B’C’) ( định nghĩa hình lăng trụ) nên d((ABC), (A’B’C’)) = d( A’, (ABC)) = A’H = a

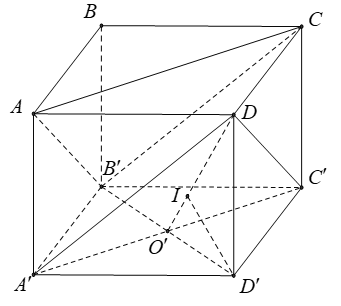
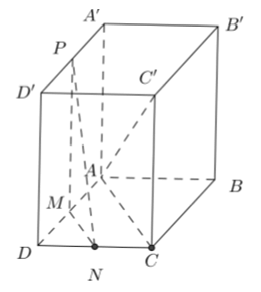
Ví dụ 2: Cho hình lập phương ABCD.A'B'C'D; cạnh a. Khoảng cách giữa (AB’C) và (A’DC’) bằng :

Hướng dẫn giải

+ Xét hai mp(AB’C) và (A’DC’) có:

+ Gọi O’ là tâm của hình vuông A’B’C’D’. Gọi I là hình chiếu của D’ trên O’D suy ra I là hình chiếu của D’ trên (A’DC’)

ta có: B’D’ = a√2 và O’D’ = (1/2)B'D' = (a√2)/2

+ xét tam giác O’D’D vuông tại D’ có:

Vậy d((AB’C) ; (A’DC’)) = (a√3)/3

Chọn đáp án D

Ví dụ 3: Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a. Gọi M, N, P lần lượt là trung điểm của AD, DC, A’D’. Tính khoảng cách giữa hai mặt phẳng(MNP) và (ACC’).

Hướng dẫn giải

Chọn D

Ta có: M và N lần lượt là trung điểm của AD và CD nên MN là đường trung bình của tam giác ADC.

⇒ MN // AC    (1)

+ Do M; P lần lượt là trung điểm của AD và A’D’ nên MP // AA’ // DD'

Lại có: CC’ // AA’ nên MP // CC’   (2)

Từ (1) và (2) suy ra: ( MNP) // (ACC’)

+ Gọi O là giao điểm của A’C’ và B’D’. Do ABCD.A’B’C’D’ là hình lăng trụ tứ giác đều nên D'O ⊥ (AA'C'C) và d(D’; (ACC’)) = D’O.

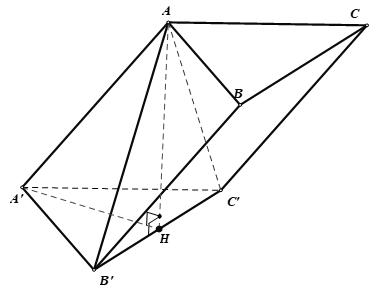
Ví dụ 4: Cho hình lăng trụ ABC.AB’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30°. Hình chiếu H của A trên mặt phẳng (A’B’C’) thuộc đường thẳng B’C’. Khoảng cách giữa hai mặt phẳng đáy là:

Hướng dẫn giải

+ Do hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a nên AB’ = AC’.

⇒ tam giác AB’C’ là tam giác cân có AH là đường cao nên đồng thời là đường trung tuyến (do AH ⊥ (A'B'C')

⇒ HB’ = HC’ và A’H = AC.sin60° = (a√3)/2

+ Do góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30° và có AH ⊥ (A’B’C’) nên ∠AA'H = 30°

Xét tam giác AA’H vuông tại H có:

AH = A’H.tan(AA'H) = (a√3)/2.tan30° = a/2

Chọn đáp án C

Ví dụ 5: Cho hình lăng trụ tam giác ABC.A’B’C’ có cạnh bên bằng a. Các cạnh bên của lăng trụ tạo với mặt đáy góc 60°. Hình chiếu vuông góc của A’lên mặt phẳng (ABC) là trung điểm của BC. Khoảng cách giữa hai mặt đáy của lăng trụ bằng bao nhiêu?

Hướng dẫn giải

Gọi H là trung điểm của BC ⇒ A’H ⊥ (ABC). Các cạnh bên của lăng trụ tạo với mặt đáy là 60° nên ∠A'AH = 60°

+ Xét tam giác A’HA vuông tại H ta có: A’H = AA’.sin60° = (a√3)/2.

+ Do (ABC) // ( A’B’C’) (định nghĩa hình lăng trụ) nên d((ABC); (A’B’C’)) = d(A’; (ABC)) = A’H = (a√3)/2

Chọn đáp án A

C. Bài tập vận dụng

Câu 1: Cho hình lập phương ABCD.A'B'C'D' cạnh a. Khoảng cách giữa (ACB’) và (DA’C’) bằng

Câu 2: Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a. Gọi M, N, P lần lượt là trung điểm của AD, DC và A’D’. Tính khoảng cách giữa hai mặt phẳng (MNP) và (ACC’)

Câu 3: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 4; AD = 3. Mặt phẳng (ACD’) tạo với mặt đáy một góc 60°. Tính khoảng cách giữa hai mặt đáy của hình hộp.

Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M, N và P lần lượt là trung điểm của các cạnh AB, AD và DC. Gọi J là trung điểm SA và H là giao điểm của CN và DM, biết SH vuông góc (ABCD), SH = a√3. Khoảng cách từ (MDJ) đến mặt phẳng (SBP) tính theo a bằng

Câu 5: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khi đó, khoảng cách giữa hai mặt phẳng (CB’D’) và (BDA’) bằng