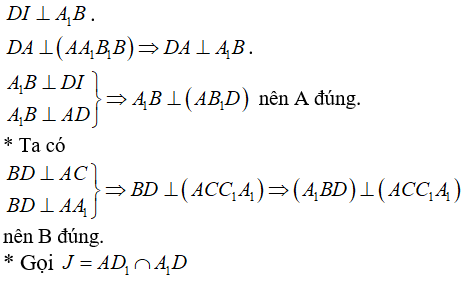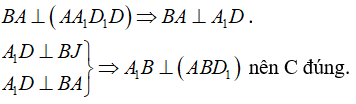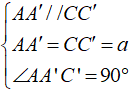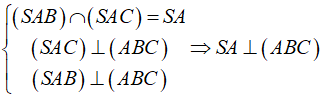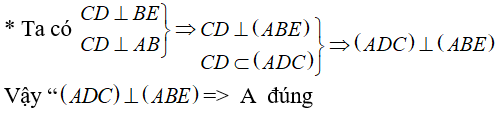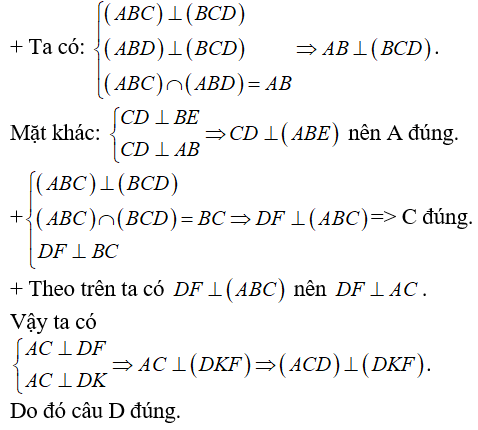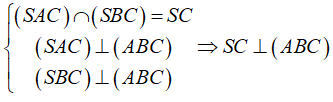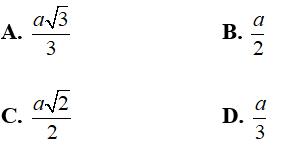Cách chứng minh hai mặt phẳng vuông góc trong không gian cực hay

A. Phương pháp giải

* Chứng minh hai mặt phẳng vuông góc

Để chứng minh (P) ⊥ (Q), ta có thể chứng minh bởi một trong các cách sau:

- Chứng minh trong (P) có một đường thẳng a mà a ⊥ (Q).

- Chứng minh ((P), (Q)) = 90°

* Chứng minh đường thẳng vuông góc với mặt phẳng

Để chứng minh d ⊥ (P), ta có thể chứng minh bởi một trong các cách sau:

- Chứng minh d ⊂ (Q) với (Q) ⊥ (P) và d vuông góc với giao tuyến c của (P) và (Q).

- Chứng minh d = (Q) ∩ (R) với (Q) ⊥ (P) và (R) ⊥ (P).

- Sử dụng các cách chứng minh đã biết ở phần trước.

B. Ví dụ minh họa

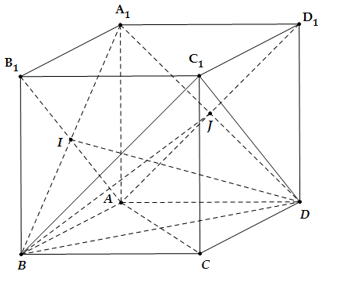
Ví dụ 1: Cho hình lập phương ABCD.A₁B₁C₁D₁ . Mặt phẳng (A₁BD) không vuông góc với mặt phẳng nào dưới đây?

A. (AB₁D)             B. (ACC₁A₁)             C. (ABD₁)             D. (A₁BC₁)

Hướng dẫn giải

* Gọi I = AB₁ ∩ A₁B

Tam giác A₁BD đều có DI là đường trung tuyến nên

Tam giác A₁BD đều có BJ là đường trung tuyến nên BJ ⊥ A₁D .

Chọn D

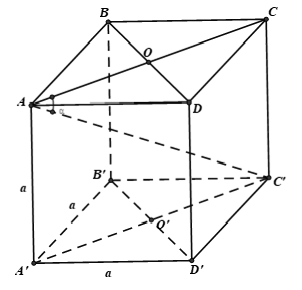
Ví dụ 2: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khẳng định nào sau đây sai?

A. Tam giác AB’C là tam giác đều.

B. Nếu α là góc giữa AC’ và ( ABCD) thì cosα = √(2/3) .

C. ACC'A' là hình chữ nhật có diện tích bằng 2a².

D. Hai mặt (AA'C'C) và (BB'D'D) ở trong hai mặt phẳng vuông góc với nhau.

Hướng dẫn giải

Chọn C

Từ giả thiết tính được AC = a√2

Mặt khác vì ABCD.A'B'C'D' là hình lập phương nên suy ra ∠AA'C' = 90°

Xét tứ giác ACC'A' có 

⇒ ACC'A' là hình chữ nhật có các cạnh a và a√2.

Diện tích hình chữ nhật ACC’A’ là :

S = a.a.√2 = a²√2   (đvdt)

⇒ đáp án C sai.

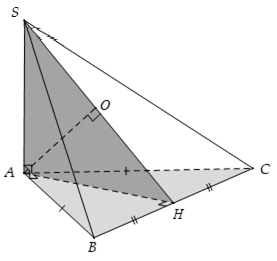
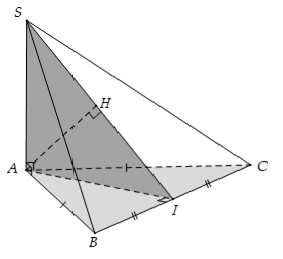
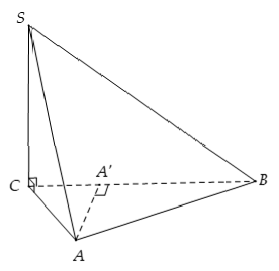
Ví dụ 3: Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với đáy (ABC) , tam giác ABC vuông cân ở A và có đường cao AH. Gọi O là hình chiếu vuông góc của A lên (SBC) . Khẳng định nào sau đây đúng?

A. SC ⊥ (ABC)

B. (SAH) ⊥ (SBC)

C. O ∈ SC

D. Góc giữa (SBC) và (ABC) là góc ∠SBA

Hướng dẫn giải

Chọn B

Ta có: 

Gọi H là trung điểm của BC ⇒ AH ⊥ BC (vì tam giác ABC vuông cân tại A).

mà BC ⊥ SA ⇒ BC ⊥ (SAH) ⇒ (SBC) ⊥ (SAH)

Khi đó O là hình chiếu vuông góc của A lên (SBC)

Thì suy ra O thuộc SH và ((SBC), (ABC)) = ∠SHA

Vậy đáp án B đúng

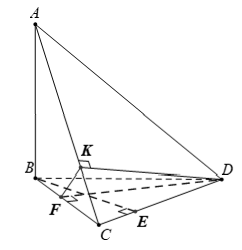
Ví dụ 4: Cho tứ diện ABCD có AB ⊥ (BCD) . Trong tam giác BDC vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ DK ⊥ AC tại K. Khẳng định nào sau đây sai ?

A. (ADC) ⊥ (ABE)           B. (ADC) ⊥ (DFK)

C. (ADC) ⊥ (ABC)            D. (BDC) ⊥ (ABE)

Hướng dẫn giải

Ta xét các phương án:

Chọn C

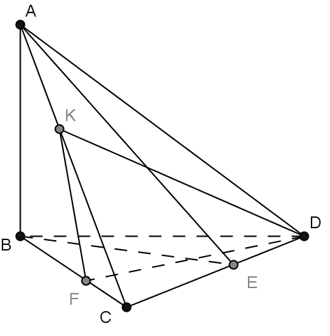
Ví dụ 5: Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC) . Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau?

A. (ABE) ⊥ (ADC)           B. (ABD) ⊥ (ADC)

C. (ABC) ⊥ (DFK)            D. (DFK) ⊥ (ADC)

Hướng dẫn giải

Chọn B

Ví dụ 6: Cho hình chóp S.ABC có SA ⊥ (ABC) và đáy ABC là tam giác cân ở A. Gọi H là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?

A. H ∈ SB

B. H trùng với trọng tâm tam giác SBC.

C. H ∈ SC

D. H ∈ SI (I là trung điểm của BC).

Hướng dẫn giải

Chọn D

Gọi I là trung điểm của BC

⇒ AI ⊥ BC mà BC ⊥ SA ⇒ BC ⊥ (SAI)

⇒ SI ⊥ BC   (1)

Khi đó H là hình chiếu vuông góc của A lên (SBC) .

Suy ra AH ⊥ BC

Lại có: SA ⊥ BC

⇒ BC ⊥ (SAH) ⇒ BC ⊥ SH    (2)

Từ (1) và (2) suy ra 3 điểm S; H; I thẳng hàng.

Chọn D.

Ví dụ 7: Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC) . Khẳng định nào sau đây sai?

A. SC ⊥ (ABC)

B. Nếu A’ là hình chiếu vuông góc của A lên ( SBC) thì A' ∈ SB .

C. (SAC) ⊥ (ABC)

D. BK là đường cao của tam giác ABC thì BK ⊥ (SAC)

Hướng dẫn giải

Chọn B

+ Ta có: 

+ Gọi A’ là hình chiếu vuông góc của A lên (SBC)

khi đó AA' ⊥ (SBC) ⇒ AA' ⊥ BC ⇒ A' ∈ BC

Suy ra đáp án B sai.

Chọn B.

C. Bài tập vận dụng

Câu 1: Cho hình chóp S.ABC có SA ⊥ (ABC) và đáy ABC vuông ở A. Khẳng định nào sau đây sai ?

A. (SAB) ⊥ (ABC)

B. (SAB) ⊥ (SAC) .

C. Vẽ AH ⊥ BC, H ∈ BC ⇒ góc AHS là góc giữa hai mặt phẳng (SBC) và (ABC) .

D. Góc giữa hai mặt phẳng (SBC) và (SAC) là góc ∠SCB

Câu 2: Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a, góc giữa hai mặt phẳng (ABCD) và (ABC’) có số đo bằng 60°. Cạnh bên của hình lăng trụ bằng:

A. 3a            B. a√3            C. 2a            D. a√2

Câu 3: Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a; CD = 2x. với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc.

Câu 4: Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Khẳng định nào sau đây sai?

A. Hai mặt ACC'A' và BDD'B' vuông góc nhau.

B. Bốn đường chéo AC’; A’C; BD’; B’D bằng nhau và bằng .

C. Hai mặt ACC’A’ và BDD’B’ là hai hình vuông bằng nhau.

D. AC ⊥ BD'

Câu 5: Cho hình lăng trụ ABCD.A'B'C'D' . Hình chiếu vuông góc của A’ lên (ABC) trùng với trực tâm H của tam giác ABC . Khẳng định nào sau đây không đúng?

A. (AA'B'B) ⊥ (BB'C'C)

B. (AA'H) ⊥ (A'B'C')

C. BB'C'C là hình chữ nhật

D. (BB'C'C) ⊥ (AA'H)