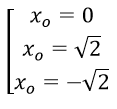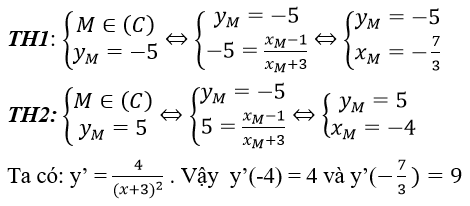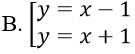Viết phương trình tiếp tuyến khi biết tiếp điểm

A. Phương pháp giải & Ví dụ

- Đường cong (C): y = f(x) có tiếp tuyến tại điểm có hoành độ x_o khi và chỉ khi hàm số y = f(x) khả vi tại x_o. Trong trường hợp (C) có tiếp tuyến tại điểm có hoành độ x_othì tiếp tuyến đó có hệ số góc f ’(x_o)

- Phương trình tiếp tuyến của đồ thị (C): y = f(x) tại điểm M(x_o; f(x_o)) có dạng :

y = f’(x_o)(x-x_o) + f(x_o)

Bài toán 1. Viết phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x_o; f(x_o))

Giải: Tiếp tuyến của đồ thị hàm số y = f(x) tại M(x_o;f(x_o)) là:

y = f’(x_o)(x-x_o)+f(x_o)        (1)

Bài toán 2. Viết phương trình tiếp tuyến của đồ thị hàm số y = f(x) biết hoành độ tiếp điểm x = x_o

Giải:

Tính y_o = f(x_o) và f’(x_o). Từ đó suy ra phương trình tiếp tuyến:

y = f’(x_o)(x-x_o) + y_o

Bài toán 3. Viết phương trình tiếp tuyến của đồ thị hàm số y = f(x) biết tung độ tiếp điểm bằng y_o

Giải. Gọi M(x_o, y_o) là tiếp điểm

Giải phương trình f(x) = y_o ta tìm được các nghiệm x_o.

Tính y’(x_o) và thay vào phương trình (1)

Ví dụ minh họa

Bài 1: Cho hàm số y = x³ + 3x² – 6x + 1 (C)

Viết phương trình tiếp tuyến của đồ thị (C) biết hoành độ tiếp điểm bằng 1

Hướng dẫn:

Gọi M(x_o; y_o) là tọa độ tiếp điểm.

Ta có x_o = 1 ⇒ y_o = - 1

y = x³ + 3x² – 6x + 1 nên y’ = 3x² + 6x – 6.

Từ đó suy ra y’(1) = 3.

Vậy phương trình tiếp tuyến cần tìm là y = 3(x – 1) – 1 = 3x – 4

Bài 2: Viết phương trình tiếp tuyến của đồ thị hàm số: y = 2x⁴ – 4x² + 1 biết tung độ tiếp điểm bằng 1

Hướng dẫn:

Gọi M(x_o; y_o) là tọa độ tiếp điểm.

Ta có y_o = 1 ⇒ 2x_o⁴ - 4x_o² + 1 = 1 ⇔ 

Ta có y’ = 8x³ – 8x

Với M(0;1) thì phương trình tiếp tuyến là: y = 0

Với M(√2;1) thì phương trình tiếp tuyến là: y = 8√2 (x - √2) + 1 = 8√2x – 15

Với M(-√2;1) thì phương trình tiếp tuyến là: y = - 8√2 (x + √2) + 1 = - 8√2x – 15

Bài 3: Cho hàm số 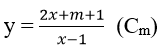. Tìm m để tiếp tuyến của (Cm) tại điểm có hoành độ x_o = 0 đi qua A(4;3)

Hướng dẫn:

x = 0 ⇒ y = - m – 1

Ta có 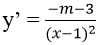. Từ đó suy ra y’(0) = - m – 3

Phương trình tiếp tuyến tại (0; - m – 1) là: y = (- m – 3)x – m – 1.

Tiếp tuyến đi qua A(4; 3) nên ta có:

3 = 4( - m – 3) – m – 1 ⇔ m = 16/5

Bài 4: Cho hàm số y = x³ – 3x + 1 (C). Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp điểm là M(0,1).

Hướng dẫn:

y’ = 3x² – 3.

y’(0) = - 3.

Phương trình tiếp tuyến cần tìm là: y = -3x – 3

Bài 5: Cho hàm số y = x⁴ + x² + 1 (C). Viết phương trình tiếp tuyến của đồ thị (C), biết hoành độ tiếp điểm là nghiệm của phương trình x² = 1.

Hướng dẫn:

Gọi M(x_o; y_o) là tọa độ tiếp điểm. Ta có:

x_o² = 1 ⇔ x_o = ±1

Ta có: y’ = 4x³ + 2x

Với M(1; 3) thì phương trình tiếp tuyến cần tìm là: y = 6(x – 1) + 3 = 6x – 3

Với M( -1; 3) thì phương trình tiếp tuyến cần tìm là y = -6(x + 1) + 3 = -6x – 3

Bài 6: Cho hàm số y = x³+3x²+1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C) :

1. Tại điểm M( -1;3)

2. Tại điểm có hoành độ bằng 2

Hướng dẫn:

Hàm số đã cho xác định D = R

Ta có: y’ = 3x² + 6x

1. Ta có: y’(-1) = -3, khi đó phương trình tiếp tuyến tại M là:

y = -3.(x + 1) + 3 = - 3x

2. Thay x = 2 vào đồ thị của (C) ta được y = 21

Tương tự câu 1, phương trình là:

y = y’(2).(x – 2) + 21 = 24x – 27

Bài 7: Gọi (C) là đồ thị của hàm số 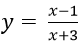. Gọi M là một điểm thuộc (C) có khoảng cách đến trục hoành độ bằng 5. Viết phương trình tiếp tuyến của (C) tại M

Hướng dẫn:

Khoảng cách từ M đến trục Ox bằng 5 ⇔ y_M = ±5.

Phương trình tiếp tuyến của (C) tại điểm M(-7/3,-5) là y = 9x + 16

Phương trình tiếp tuyến của (C) tại điểm M( - 4, 5) là y = 4x + 21

B. Bài tập vận dụng

Bài 1: Phương trình tiếp tuyến của đồ thị của hàm số y = x(3 – x)² tại điểm có hoành độ x = 2 là

A. y = -3x + 8

B. y = -3x + 6

C. y = 3x – 8

D. y = 3x – 6

Bài 2: Cho đường cong (C): y = x². Phương trình tiếp tuyến của (C) tại điểm M( -1; 1) là

A. y = -2x + 1.

B. y = 2x + 1.

C. y = -2x - 1.

D. y = 2x – 1.

Bài 3: Cho hàm số 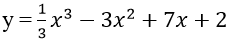. Phương trình tiếp tuyến tại A(0 ; 2) là:

A. y = 7x + 2

B. y = 7x - 2

C. y = - 7x + 2

D. y = - 7x - 2

Bài 4: Gọi (P) là đồ thị của hàm số y = 2x² – x + 3. Phương trình tiếp tuyến với (P) tại điểm mà (P) cắt trục tung là:

A. y = - x + 3

B. y = - x - 3

C. y = 4x – 1

D. y = 11x + 3

Bài 5: Cho hàm số 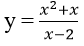. Phương trình tiếp tuyến tại A(1; -2) là

A. y = - 4( x – 1) – 2

B. y = - 5( x – 1) + 2

C. y = - 5( x – 1) – 2

D. y = -3(x – 1) – 2

Bài 6: Cho hàm số y = f(x), có đồ thị (C) và điểm M_o(x_o ; f(x_o)) ∈ (C). Phương trình tiếp tuyến của (C) tại M_o là:

A. y = f'(x)(x-x_o )+y_o

B. y = f'(x_o )(x-x_o )

C. y - y_o = f'(x_o)(x-x_o )

D. y - y_o = f'(x_o )x

Bài 7: Tiếp tuyến của đồ thị hàm số 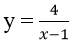 tại điểm có hoành độ x_o = -1 có phương trình là:

A. y = - x + 2

B. y = x + 2

C. y = x – 1

D. y = - x – 3

Bài 8: Phương trình tiếp tuyến của đồ thị hàm số y = x⁴ + 2x² – 1 tại điểm có tung độ tiếp điểm bằng 2 là:

A. y = 8x – 6, y = -8x – 6

B. y = 8x – 6, y = -8x + 6

C. y = 8x – 8, y = -8x + 8

D. y = 40x – 57

Bài 9: Phương trình tiếp tuyến của đồ thị hàm số y = (x + 1)²(x – 2) tại điểm có hoành độ x = 2 là

A. y = - 8x + 4

B. y = 9x + 18

C. y = -4x + 4

D. y = 9x – 18

Bài 10: Đồ thị (C) của hàm số 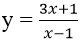 cắt trục tung tại điểm A. Tiếp tuyến của (C) tại điểm A có phương trình là:

A. y = - 4x – 1.

B. y = 4x – 1.

C. y = 5x – 1.

D. y = - 5x – 1.

Bài 11: Cho hàm số 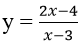 có đồ thị là (H). Phương trình tiếp tuyến tại giao điểm của (H) với trục hoành là:

A. y = 2x – 4.

B. y = 3x + 1.

C. y = - 2x + 4.

D. y = 2x.

Bài 12: Lập phương trình tiếp tuyến của đồ thị (H): 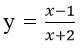 tại giao điểm của (H) và trục hoành:

A. y = (1/3)(x-1)

B. y = 3x

C. y = x – 3

D. y = 3(x – 1)

Bài 13: Gọi (P) là đồ thị hàm số y = x² – x + 3. Phương trình tiếp tuyến với (P) tại giao điểm của (P) và trục tung là

A. y = -x + 3

B. y = -x - 3

C. y = x - 3

D. y = -3x + 1

Bài 14: Phương trình tiếp tuyến của đồ thị hàm số f(x) = x³ – 2x² + 3x tại điểm có hoành độ x_o = -1 là:

A. y = 10x + 4

B. y = 10x – 5

C. y = 2x – 4

D. y = 2x – 5

Bài 15: Gọi (H) là đồ thị hàm số 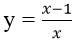. Phương trình tiếp tuyến của đồ thị (H) tại các giao điểm của (H) với hai trục toạ độ là:

A. y = x – 1

C. y = - x + 1

D. y = x + 1