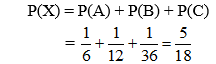Biến cố xung khắc là gì? Bài tập biến cố xung khắc cực hay, chi tiết

Với Biến cố xung khắc là gì? Bài tập biến cố xung khắc cực hay, chi tiết Toán học lớp 11 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Biến cố xung khắc là gì? Bài tập biến cố xung khắc cực hay, chi tiết.

1827

Tải tài liệu

« Trang trước

Trang sau »

Biến cố xung khắc là gì? Bài tập biến cố xung khắc cực hay, chi tiết

1. Định nghĩa

- Định nghĩa: Cho hai biến cố A và B. Hai biến cố A và B được gọi là xung khắc nếu biến cố này xảy ra thì biến cố kia không xảy ra.

- Hai biến cố A và B là hai biến cố xung khắc nếu và chỉ nếu Ω_A ∩ Ω_B = ∅.

2. Quy tắc cộng xác suất

- Nếu hai biến cố A và B xung khắc thì xác suất để A hoặc B xảy ra là

P(A ∪ B) = P(A) + P(B)

- Quy tắc cộng xác suất cho nhiều biến cố:

Cho k biến cố A₁, A₂, …, A_k đôi một xung khắc. Khi đó

P(A₁ ∪ A₂ ∪ … ∪ A_k) = P(A₁) + P(A₂) + … + P(A_k)

3. Ví dụ

Ví dụ 1. Cho hai biến cố A và B. biết P(A) = 0,21; P(B) = 0,11 và P(A ∪ B) = 0,3. Hỏi A và B có phải là hai biến cố xung khắc không?

Hướng dẫn:

Ta có: P(A) + P(B) = 0,21 + 0,11 = 0,32 ≠ 0,3 = P(A ∪ B)

Suy ra P(A) + P(B) ≠ P(A ∪ B)

Theo quy tắc cộng xác suất của hai biến cố xung khắc, vậy hai biến cố A và B không xung khắc.

Ví dụ 2. Tung một con xúc xắc, gọi A là biến cố: “Xuất hiện mặt có chấm số chấm lớn hơn hoặc bằng 4”, B là biến cố: “Xuất hiện mặt có chấm số chấm nhỏ hơn hoặc bằng 2”.

Ta thấy hai biến cố và không cùng xảy ra, do đó A và B là hai biến cố xung khắc.

Ví dụ 3. Một hộp đựng 4 viên bi xanh,3 viên bi đỏ và 2 viên bi vàng.Chọn ngẫu nhiên 2 viên bi. Tính xác suất để chọn được hai viên bi cùng màu.

Hướng dẫn:

Có tất cả: 4 + 3 + 2 = 9 viên bi

Biến cố xung khắc là gì? Bài tập biến cố xung khắc cực hay, chi tiết - Toán lớp 11