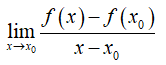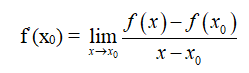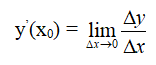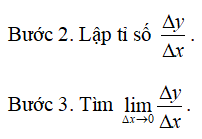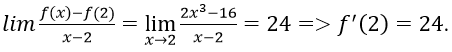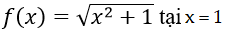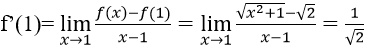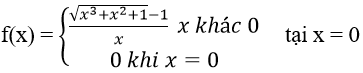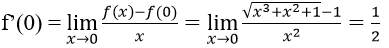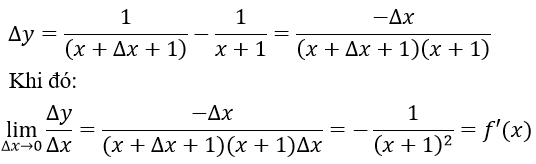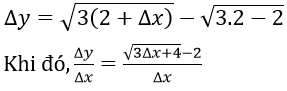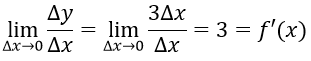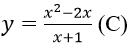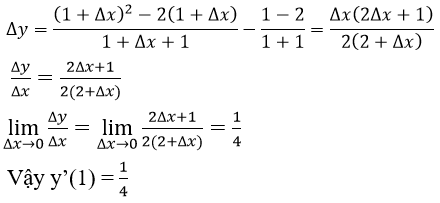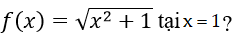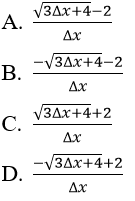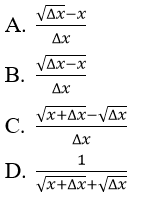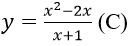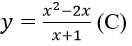Phương pháp tính đạo hàm bằng định nghĩa hay, chi tiết

A. Phương pháp giải & Ví dụ

1. Định nghĩa đạo hàm tại một điểm

    Cho hàm số y = f(x) xác định trên khoảng (a; b) và x₀ ∈ (a; b). Nếu tồn tại giới hạn (hữu hạn)

thì giới hạn đó được gọi là đạo hàm của hàm số y = f(x) tại x₀ và kí hiệu là f’(x₀) (hoặc y’(x₀)), tức là

Chú ý:

    Đại lượng Δx = x – x₀ gọi là số gia của đối số x tại x₀.

    Đại lượng Δy = f(x) – f(x₀) = f(x₀ + Δx) – f(x₀) được gọi là số gia tương ứng của hàm số. Như vậy

2. Cách tính đạo hàm bằng định nghĩa

    Bước 1. Giả sử Δx là số gia của đối số x tại x₀, tính Δy = f(x₀ + Δx) – f(x₀).

Chú ý: Trong định nghĩa trên đây, thay x_o bởi x ta sẽ có định nghĩa và quy tắc tính đạo hàm của hàm số y = f(x) tại điểm x ∈ (a, b)

Ví dụ minh họa

Bài 1: Tính đạo hàm của các hàm số sau tại các điểm đã cho: f(x)= 2x³ + 1 tại x = 2

Hướng dẫn:

Ta có

Bài 2: Tính đạo hàm của các hàm số sau tại các điểm đã cho:

Hướng dẫn:

Ta có

Bài 3: Tính đạo hàm của hàm số:

Hướng dẫn:

Ta có f(0) = 0, do đó:

Bài 4: Tính đạo hàm của hàm số 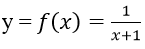 bằng định nghĩa

Hướng dẫn:

Tập xác định của hàm số đã cho là D = R\{-1}

Ta có

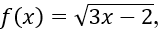
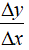
Bài 5: Cho hàm số  có Δx là số gia của đối số tại x = 2. Khi đó  bằng bao nhiêu?

Hướng dẫn:

Tập xác định của hàm số đã cho là D = [2/3; +∞)

Với Δx là số gia của đối số tại x = 2 sao cho 2 + Δx ∈ D, thì

Bài 6: Cho hàm số f(x) = 3x + 5.Tính đạo hàm của hàm số đã cho bằng định nghĩa.

Hướng dẫn:

Tập xác định của hàm số đã cho là D = R

Ta có Δy = 3(x+Δx) + 5 - 3x - 5 = 3Δx

Khi đó:

Bài 7: Cho hàm số 

Đạo hàm của hàm số đã cho tại x = 1?

Hướng dẫn:

với Δx là số gia của đối số tại x = 1, ta có

B. Bài tập vận dụng

Bài 1: Đạo hàm của các hàm số sau tại các điểm đã cho:

A. 1/2            B. -1/√2            C. 0             D. 3

Bài 2: Hàm số 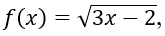 có Δx là số gia của đối số tại x = 2. Khi đó Δy/Δx bằng?

Bài 3: Số gia của hàm số f(x) = 2x² - 1 tại x₀ = 1 ứng với số gia Δx = 0,1 bằng:

A. 1

B. 1,42

C. 2,02

D. 0,42

Bài 4: Cho hàm số y = √x, Δx là số gia của đối số tại x. Khi đó Δy/Δx bằng:

Bài 5: Cho hàm số 

Đạo hàm của hàm số đã cho tại x = 1?

A. 1            B. 0            C. 1/4            D. -1/4

Bài 6: Đạo hàm của các hàm số sau tại các điểm đã cho: f(x) = 2x³ + 1 tại x = 2?

A. 10

B. 24

C. 22

D. 42

Bài 7: Cho hàm số f(x) = x² + 2x, có Δx là số gia của đối số tại x = 1, Δy là số gia tương ứng của hàm số. Khi đó Δy bằng:

A. (Δx)² + 2Δx

B. (Δx)² + 4Δx

C. (Δx)² + 2Δx - 3

D. 3

Bài 8: Cho hàm số 

Đạo hàm của hàm số đã cho tại x = 1 là:

A. 1/4            B. -1/2            C. 0            D. 1/2

Bài 9: Cho hàm số f(x) = |x + 1|. Khẳng định nào sau đây là sai?

A. f(x) liên tục tại x = -1

B. f(x) có đạo hàm tại x = -1

C. f(-1) = 0

D. f(x) đạt giá trị nhỏ nhất tại x = -1

Bài 10: Đạo hàm của các hàm số sau tại các điểm đã cho: f(x) = x² + 1 tại x = 1?

A. 1/2            B. 1            C. 0            D. 2