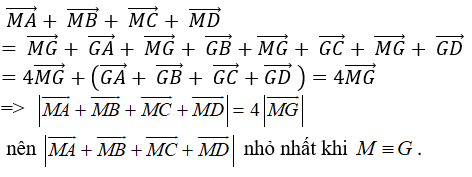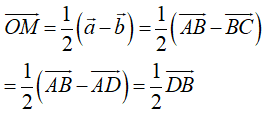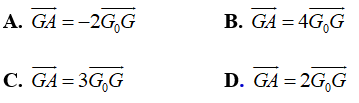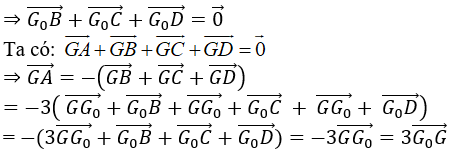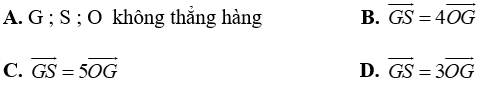Cách tìm tập hợp điểm thỏa mãn đẳng thức vectơ cực hay

A. Phương pháp giải

+ Tập hợp các điểm M sao cho MA = k - không đổi là hình cầu tâm A bán kính R = k.

+ Tập hơp các điểm M sao cho MA→ + MB→ = 0→ là trung điểm của đoạn thẳng AB.

+ Nếu MA→ = k.BC→ trong đó A ; B ; C là các điểm đã biết thì điểm M cần tìm nằm trên đường thẳng qua A song song (hoặc trùng BC) và MA = |k|.BC

B. Ví dụ minh họa

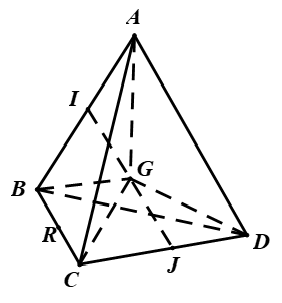
Ví dụ 1: Cho tứ diện ABCD . Gọi I; J lần lượt là trung điểm của AB và CD, G là trung điểm của IJ. Xác định vị trí của M để |MA→ + MB→ + MC→ + MD→| nhỏ nhất

A. Trung điểm AB

B. Trùng với G

C. Trung điểm AC

D. Trung điểm CD

Hướng dẫn giải

Ta có:

Ví dụ 2: Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD. Điểm M xác định bởi đẳng thức vectơ AM→ = AB→ + AC→ + AD→. Mệnh đề nào sau đây đúng?

A. M trùng G

B. M thuộc tia AG và AM = 3AG

C. G là trung điểm AM

D. M là trung điểm AG

Hướng dẫn giải

Do G là trọng tâm tam giác BCD nên AB→ + AC→ + AD→ = 3AG→

Kết hợp giả thiết, suy ra AM→ = 3AG→

⇒ M thuộc tia AG và AM = 3AG

Chọn B

Ví dụ 3: Cho tứ diện ABCD. Điểm N xác định bởi AN→ = AB→ + AC→ - AD→. Mệnh đề nào sau đây đúng?

A. N là trung điểm BD.

B. N là đỉnh thứ tư của hình bình hành BCDN.

C. N là đỉnh thứ tư của hình bình hành CDBN.

D. N trùng với A.

Hướng dẫn giải

Theo giả thiết ta có: AN→ = AB→ + AC→ - AD→ ⇔ AN→ - AB→ = AC→ - AD→ ⇔ BN→ = DC→

Đẳng thức chứng tỏ N là đỉnh thứ tư của hình bình hành CDBN

Chọn C.

Ví dụ 4: Cho hình hộp ABCD. A’B’C’D’ có tâm. Đặt AB→ = a→, BC→ = b→. Gọi M là điểm xác định bởi OM→ = (1/2).(a→ - b→). Khẳng định nào sau đây đúng?

A. M là tâm hình bình hành ABB’A’

B. M là tâm hình bình hành BCC’B’

C. M là trung điểm BB’

D. M là trung điểm CC’

Hướng dẫn giải

Chọn C.

Ta phân tích:

→ OM // DB và OM = 1/2 DB

→ M là trung điểm của BB’

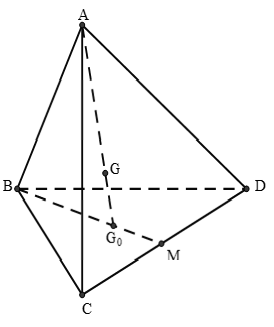
Ví dụ 5: Cho tứ diện ABCD và điểm G thỏa mãn GA→ + GB→ + GC→ + GD→ = 0→. (G là trọng tâm của tứ diện). Gọi G₀ là giao điểm của GA và mp (BCD) . Trong các khẳng định sau, khẳng định nào đúng?

Hướng dẫn giải

Chọn C

Theo đề: G₀ là giao điểm của GA và mp (BCD)

⇒ G₀ là trọng tâm tam giác BCD.

C. Bài tập vận dụng

Câu 1: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi G là điểm thỏa mãn: GS→ + GA→ + GB→ + GC→ + GD→ = 0→. Trong các khẳng định sau, khẳng định nào đúng?

Câu 2: Cho hình hộp ABCD.A’B’C’D’. Điểm M được xác định bởi đẳng thức vectơ MA→ + MB→ + MC→ + MD→ + MA'→ + MB'→ + MC'→ + MD'→ = 0→. Mệnh đề nào sau đây đúng?

A. M là tâm của mặt đáy ABCD

B. M là tâm của mặt đáy A’B’C’D’.

C. M là trung điểm của đoạn thẳng nối hai tâm của hai mặt đáy.

D. Tập hợp điểm M là đoạn thẳng nối hai tâm của hai mặt đáy.

Câu 3: Trong không gian cho tam giác ABC. Tìm M sao cho giá trị của biểu thức P = MA² + MB² + MC² đạt giá trị nhỏ nhất.

A. M là trọng tâm tam giác ABC.

B. M là tâm đường tròn ngoại tiếp tam giác ABC.

C. M là trực tâm tam giác BAC

D. M là tâm đường tròn nội tiếp tam giác ABC.

Câu 4: Cho tứ diện ABCD. Người ta định nghĩa “G là trọng tâm tứ diện ABCD khi GA→ + GB→ + GC→ + GD→ = 0→. Khẳng định nào sau đây sai?

A. G là trung điểm của đoạn IJ (I; J lần lượt là trung điểm AB và CD).

B. G là trung điểm của đoạn thẳng nối trung điểm của AC và BD.

C. G là trung điểm của đoạn thẳng nối trung điểm của AD và BC.

D. Chưa thể xác định được.

Câu 5: Cho hình hộp ABCD. A’B’C’D’ có tâm. Đặt AB→ = a→, BC→ = b→. Gọi M là điểm xác định bởi OM→ = (1/2).(a→ - b→). Khẳng định nào sau đây đúng?

A. M là tâm hình bình hành ABB’A’

B. M là tâm hình bình hành BCC’B’

C. M là trung điểm BB’

D. M là trung điểm CC’