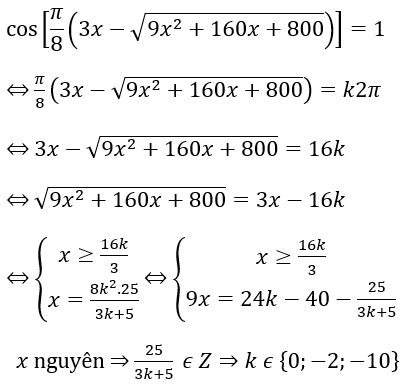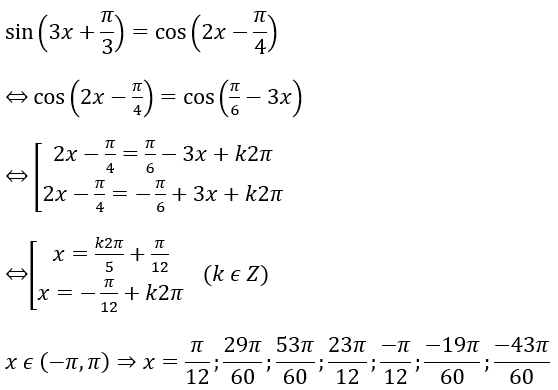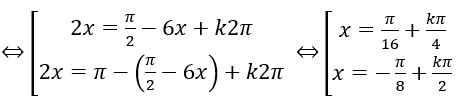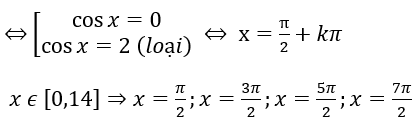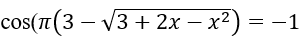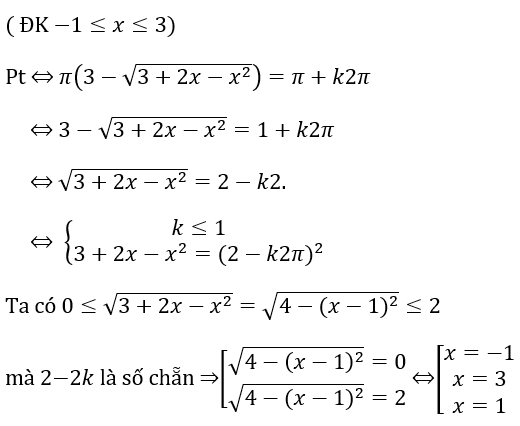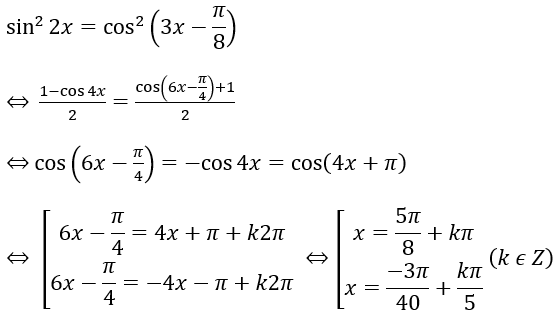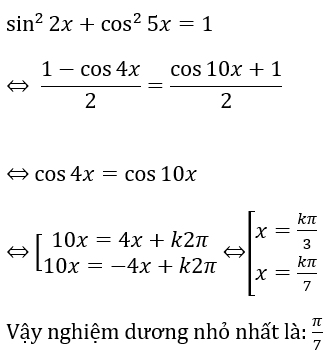Tìm nghiệm của phương trình lượng giác thỏa mãn điều kiện
Với Tìm nghiệm của phương trình lượng giác thỏa mãn điều kiện Toán học lớp 11 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học sinh nắm được Tìm nghiệm của phương trình lượng giác thỏa mãn điều kiện.
Tìm nghiệm của phương trình lượng giác thỏa mãn điều kiện
A. Ví dụ
Bài 1: Tìm nghiệm nguyên của phương trình:
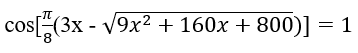
Thử lại ta có các nghiệm nguyên: x=-7 (k=-2); x=-31 (k=10)
Bài 2: Tìm tổng các nghiệm của phương trình sin(3x + π/3) = cos(2x - π/4) trong khoảng (- π , π )
Vậy tổng các nghiệm là: 9π/4

B. Bài tập vận dụng
Bài 1: Tìm nghiệm âm lớn nhất của phương trình: (sinx + cosx)2 = 2cos23x.
Lời giải:
(sinx + cosx )2 = 2 cos23x
⇔ 1 + sin 2x = cos6x+1
⇔ sin2x = cos6x
Vậy nghiệm dương nhỏ nhất là: (-π)/8
Bài 2: Tìm x ∈ [0,14] nghiệm đúng phương trình : cos3x – 4cos2x + 3cosx – 4 = 0.
Lời giải:
cos3x- 4 cos2x + 3 cosx - 4 = 0
⇔ 4 cos3x - 3 cosx- 8 cos2x + 4 + 3 cosx - 4 = 0
Bài 3: Tìm nghiệm nguyên dương của phương trình:
Lời giải:
Bài 4: Tìm tổng các nghiệm của phương trình sin22x = cos2(3x - π/8) trong khoảng (- π , π )
Lời giải:
x ∈ (-π ,π ) ⇒ x = 5π /8; (-7π )/8; (-27π )/40; (-19π )/40; (-11π )/40; (-3π )/40; π /8; 13π /40; 21π /40; 29π /40; 37π /40
Tổng các nghiệm là: 7π/8
Bài 5: Tìm nghiệm dương nhỏ nhất của phương trình: sin22x + cos25x = 1.
Lời giải: