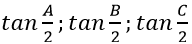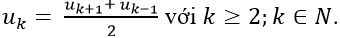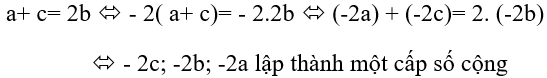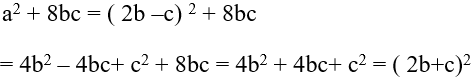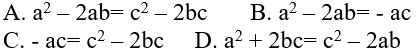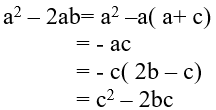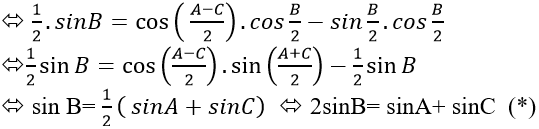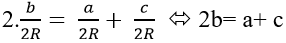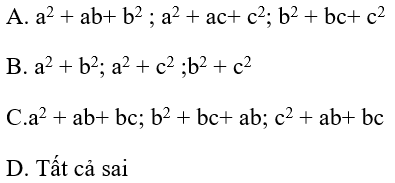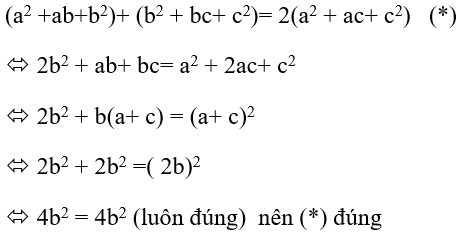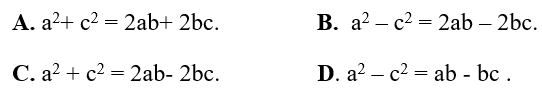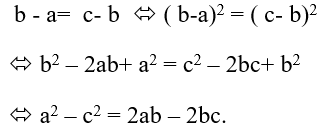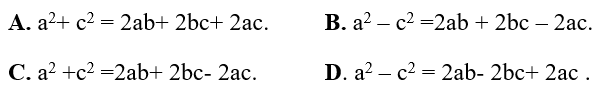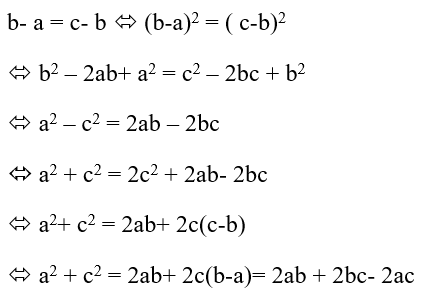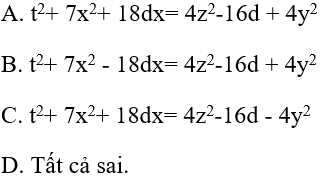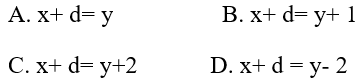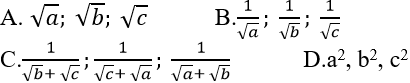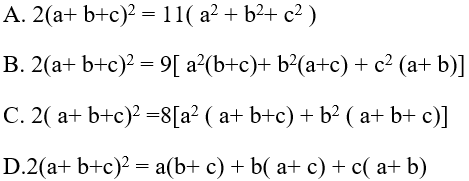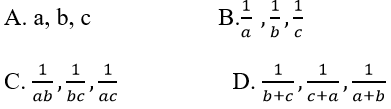Cách chứng minh đẳng thức dựa vào tính chất của cấp số cộng cực hay

A. Phương pháp giải

* Tính chất của cấp số cộng: Cho (u_n) là cấp số cộng thì ta có

* Nếu ba số a; b; c lập thành cấp số cộng thì c − b = b − a.

B. Ví dụ minh họa

Ví dụ 1: Cho 3 số a; b và c theo thứ tự lập thành cấp số cộng, ba số nào dưới đây cũng lập thành một cấp số cộng ?

Hướng dẫn giải:

Ta có a,b,c theo thứ tự lập thành cấp số cộng khi và chỉ khi:

Chọn B

Ví dụ 2: Cho a,b và c là ba số hạng liên tiếp của một cấp số cộng. Tìm đẳng thức đúng?

Hướng dẫn giải:

+ Ta có a,b và c theo thứ tự lập thành cấp số cộng nên : a + c = 2b ⇔ a = 2b – c

+ Khi đó;

Chọn C.

Ví dụ 3: Cho ba số a,b,c là ba số hạng liên tiếp của một cấp số cộng .Đẳng thức nào sau đây sai?

Hướng dẫn giải:

Vì a, b, c là ba số hạng liên tiếp của một cấp số cộng nên: a + c= 2b ⇔ a = 2 b - c

Ta có:

Vậy a² − 2ab = c² − 2bc ; a² − 2ab = −ac và −ac = c² − 2bc

Chọn D.

Ví dụ 4: Cho tam giác ABC có cot 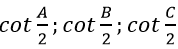 theo thứ tự lập thành cấp số cộng. Tìm hệ thức đúng về mối liên hệ giữa ba cạnh a,b và c?

Hướng dẫn giải:

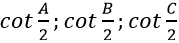
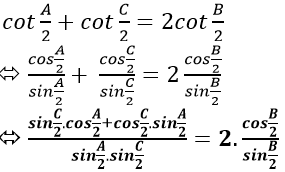
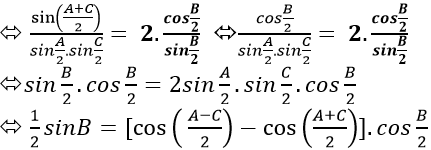
Do  theo thứ tự lập thành cấp số cộng nên:

Áp dụng định lí sin trong tam giác suy ra:

 thay vào (*) ta được:

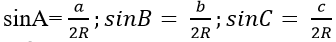
=> Ba cạnh của tam giác ABC tạo thành cấp số cộng.

Chọn D.

Ví dụ 5: Cho ba số a, b và c theo thứ tự lập thành cấp số cộng. Ba số nào sau đây cũng lập thành cấp số cộng.

Hướng dẫn giải:

Ta chứng minh ba số: a² + ab + b²; a² + ac + c² ; b² + bc + c² theo thứ tự lập thành cấp số cộng.

Thật vậy;

=> ba số: a² + ab + b²; a² + ac + c² ; b² + bc + c² theo thứ tự lập thành cấp số cộng.

Chọn A.

Ví dụ 6: Cho a, b, c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?

Hướng dẫn giải:

Ta có a, b, c theo thứ tự lập thành cấp số cộng khi và chỉ khi:

Chọn B

Ví dụ 7: Cho 3 số a; b và c theo thứ tự lập thành cấp số cộng, đẳng thức nào sau đây là đúng?

Hướng dẫn giải:

Ta có 3 số a,b,c theo thứ tự lập thành cấp số cộng khi và chỉ khi:

Chọn C.

C. Bài tập trắc nghiệm

Câu 1: Cho bốn số x, y, z và t theo thứ tự lập thành cấp số cộng. Hỏi đẳng thức nào sau đây là đúng?

Câu 2: Cho ba số x + 1; y + 3 và z - 3 theo thứ tự lập thành cấp số cộng. Tìm mệnh đề đúng?

Câu 3: Cho ba số a, b và c dương theo thứ tự lập thành cấp số cộng. Ba số nào sau đây cũng lập thành cấp số cộng.

Câu 4: Cho a,b và c là 3 số hạng liên tiếp của một cấp số cộng. Hỏi ba số nào sau đây cũng là cấp số cộng.

Câu 5: Cho ba số a,b,c theo thứ tự lập thành cấp số cộng. Đẳng thức nào sau đây đúng?

Câu 6: Cho ba số x- 1; y+ 1 và z theo thứ tự lập thành cấp số cộng. Tìm mệnh đề đúng?

Câu 7: Cho các số a², b² và c² lập thành một cấp số cộng có công sai d khác không. Ba số nào sau đây cũng lập thành cấp số cộng.

Câu 8: Cho tam giác ABC có tan  theo thứ tự đó lập thành cấp số cộng. Hỏi 3 số nào sau đây cũng lập thành cấp số cộng.