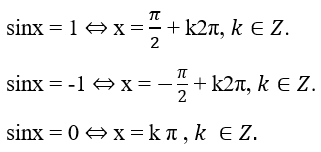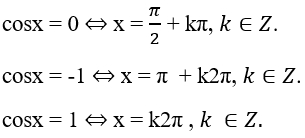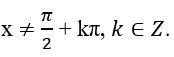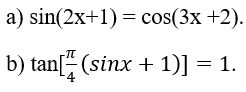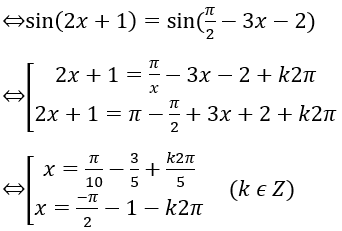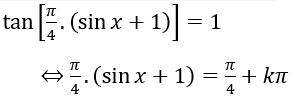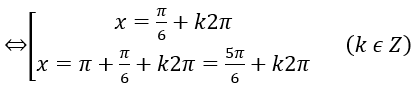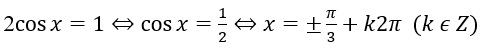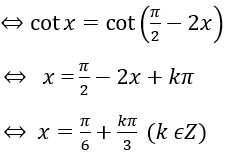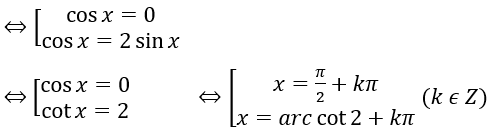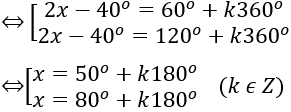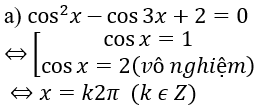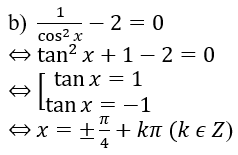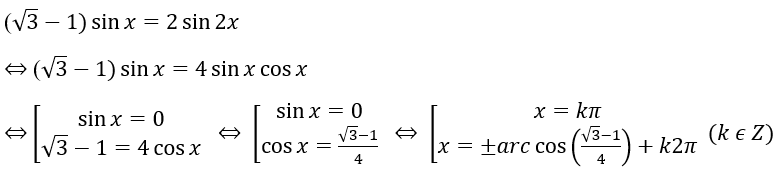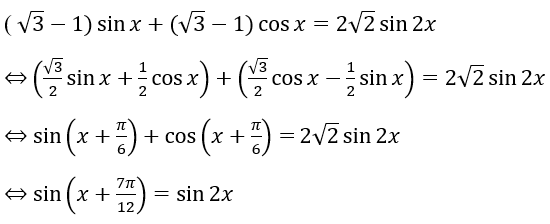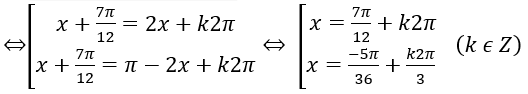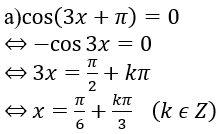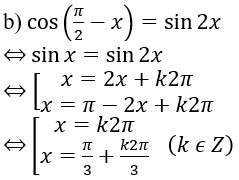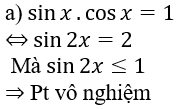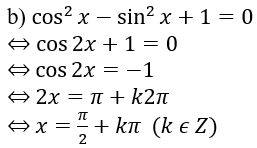Cách giải phương trình lượng giác cơ bản

A. Phương pháp giải & Ví dụ

- Phương trình sinx = a        (1)

    ♦ |a| > 1: phương trình (1) vô nghiệm.

    ♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.

Khi đó phương trình (1) có các nghiệm là

                x = α + k2π, k ∈ Z

                và x = π-α + k2π, k ∈ Z.

Nếu α thỏa mãn điều kiện 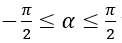 và sinα = a thì ta viết α = arcsin a.

Khi đó các nghiệm của phương trình (1) là

                x = arcsina + k2π, k ∈ Z

                và x = π - arcsina + k2π, k ∈ Z.

Các trường hợp đặc biệt:

- Phương trình cosx = a        (2)

    ♦ |a| > 1: phương trình (2) vô nghiệm.

    ♦ |a| ≤ 1: gọi α là một cung thỏa mãn cosα = a.

Khi đó phương trình (2) có các nghiệm là

                x = α + k2π, k ∈ Z

                và x = -α + k2π, k ∈ Z.

Nếu α thỏa mãn điều kiện 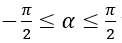 và cosα = a thì ta viết α = arccos a.

Khi đó các nghiệm của phương trình (2) là

                x = arccosa + k2π, k ∈ Z

                và x = -arccosa + k2π, k ∈ Z.

Các trường hợp đặc biệt:

- Phương trình tanx = a        (3)

Điều kiện: 

Nếu α thỏa mãn điều kiện 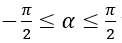 và tanα = a thì ta viết α = arctan a.

Khi đó các nghiệm của phương trình (3) là

                x = arctana + kπ,k ∈ Z

- Phương trình cotx = a        (4)

Điều kiện: x ≠ kπ, k ∈ Z.

Nếu α thỏa mãn điều kiện 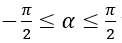 và cotα = a thì ta viết α = arccot a.

Khi đó các nghiệm của phương trình (4) là

                x = arccota + kπ, k ∈ Z

B. Ví dụ minh họa

Bài 1: Giải các phương trình lượng giác sau:

Bài 2: Giải các phương trình lượng giác sau:

a) sinx = sin(π/6)        c) tanx – 1 = 0

b) 2cosx = 1.        d) cotx = tan2x.

Bài 3: Giải các phương trình lượng giác sau:

a) cos² x - sin2x =0.

b) 2sin(2x – 40º) = √3

Đáp án và hướng dẫn giải

Bài 1: Giải các phương trình lượng giác sau:

a) sin⁡(2x+1)=cos⁡(3x+2)

b)

⇔ sin⁡x+1=1+4k

⇔ sin⁡x=4k (k ∈ Z)

Nếu |4k| > 1⇔|k| > 1/4; phương trình vô nghiệm

Nếu |4k| ≤ 1 mà k nguyên ⇒ k = 0 .Khi đó:

        ⇔sin⁡x = 0 ⇔ x = mπ (m ∈ Z)

Bài 2: Giải các phương trình lượng giác sau:

a) sin⁡x = sin⁡π/6

b)

c) tan⁡x=1⇔cos⁡x= π/4+kπ (k ∈ Z)

d) cot⁡x=tan⁡2x

Bài 3: Giải các phương trình lượng giác sau:

a) cos²x-sin²x=0 ⇔cos²x-2 sin⁡x cos⁡x=0

        ⇔ cos⁡x (cos⁡x - 2 sin⁡x )=0

b) 2 sin⁡(2x-40º )=√3

⇔ sin⁡(2x-40º )=√3/2

C. Bài tập vận dụng

Bài 1: Giải các phương trình sau

a) cos² x - 3cosx + 2 = 0

b) 1/(cos² x) - 2 = 0.

Lời giải:

Bài 2: Giải các phương trình sau: (√3-1)sinx = 2sin2x.

Lời giải:

Bài 3: Giải các phương trình sau: (√3-1)sinx + (√3+1)cosx = 2√2 sin2x

Lời giải:

Bài 4: Giải các phương trình sau

a) cos(3x + π) = 0

b) cos (π/2 - x) = sin2x

Lời giải:

Bài 5: Giải các phương trình sau

a) sinx.cosx = 1

b) cos² x - sin² x + 1 = 0

Lời giải: