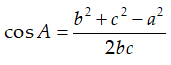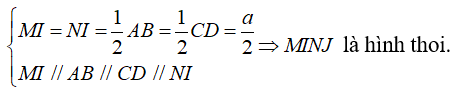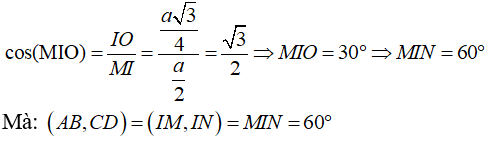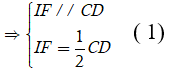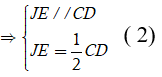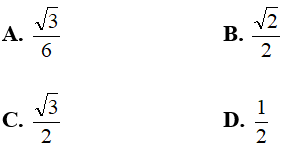Cách xác định góc giữa hai vecto, góc giữa hai đường thẳng cực hay

A. Phương pháp giải

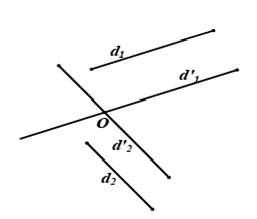
Để tính góc giữa hai đường thẳng d₁; d₂ trong không gian ta có thể thực hiện theo hai cách

Cách 1. Tìm góc giữa hai đường thẳng d₁, d₂ bằng cách chọn một điểm O thích hợp (O thường nằm trên một trong hai đường thẳng).

Từ O dựng các đường thẳng d₁, d₂ lần lượt song song ( có thể tròng nếu O nằm trên một trong hai đường thẳng) với d₁ và d₂. Góc giữa hai đường thẳng d₁, d₂ chính là góc giữa hai đường thẳng d₁, d₂.

Lưu ý 1: Để tính góc này ta thường sử dụng định lí côsin trong tam giác

Cách 2. Tìm hai vec tơ chỉ phương u₁, u₂ của hai đường thẳng d₁, d₂

Khi đó góc giữa hai đường thẳng d₁, d₂ xác định bởi cos(d₁, d₂) = 

Lưu ý 2: Để tính u₁→, u₂→, |u₁→|, |u₂→| ta chọn ba vec tơ a→, b→, c→ không đồng phẳng mà có thể tính được độ dài và góc giữa chúng,sau đó biểu thị các vec tơ u₁→, u₂→ qua các vec tơ a→, b→, c→ rồi thực hiện các tính toán.

B. Ví dụ minh họa

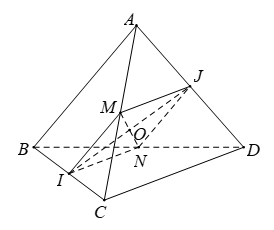
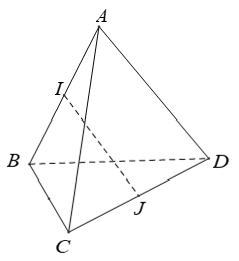
Ví dụ 1: Cho tứ diện ABCD có AB = CD = a, IJ = (a√3)/2 (I; J lần lượt là trung điểm của BC và AD). Số đo góc giữa hai đường thẳng AB và CD là

A. 30°               B. 45°               C. 60°               D. 90°

Hướng dẫn giải

Chọn C

Gọi M; N lần lượt là trung điểm AC; BC.

Ta có:

Gọi O là giao điểm của MN và IJ.

Ta có: ∠MIN = 2∠MIO .

Xét tam giác MIO vuông tại O, ta có:

Ví dụ 2: Cho tứ diện ABCD có AB = AC = AD và

. Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ AB→ và IJ→ ?

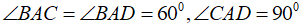
A. 120°               B. 90°               C. 60°               D.45°

Hướng dẫn giải

Chọn B

+ Xét tam giác ABC có AB = AC và ∠BAC = 60° nên tam giác ABC đều

Tương tự tam giác ABD đều.

⇒ BC = BD (= AB)

+ Xét tam giác ACD và tam giác BCD có :

BC = AC.

AD = BD

CD chung

⇒ Δ BCD = Δ ACD( c.c.c) ⇒ BJ = AJ

⇒ Tam giác AJB là tam giác cân tại J. Lại có, JI là đường trung tuyến nên đồng thời là đường cao.

⇒ IJ ⊥ AB.

⇒ góc giữa cặp vectơ AB→ và IJ→ là 90°

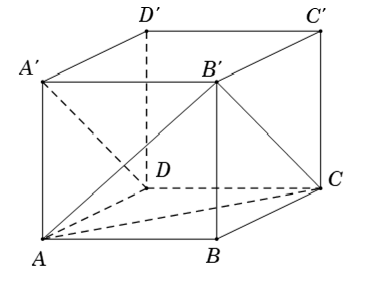
Ví dụ 3: Cho hình lập phương ABCD.A’B’C’D’. Góc giữa AC và DA’ là:

A. 45°               B. 90°               C. 60°               D. 120°

Hướng dẫn giải

Gọi a là độ dài cạnh hình lập phương

Khi đó, tam giác AB’C đều (AB' = B'C = CA = a√2) do đó ∠B'CA= 60° .

Lại có, DA’ song song CB’ nên

(AC, DA') = (AC, CB') = ∠ACB'= 60°.

Chọn C

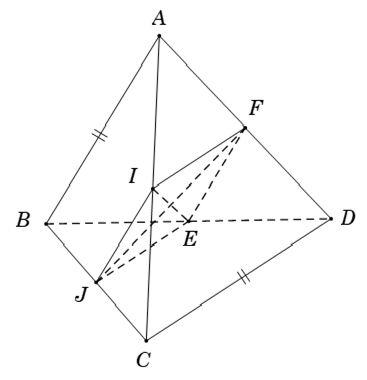
Ví dụ 4: Cho tứ diện ABCD có BA = CD. Gọi I ; J ; E ; F lần lượt là trung điểm của AC ; BC ; BD ; AD. Góc (IE; JF) bằng

A. 30°               B. 45°               C. 60°               D. 90°

Hướng dẫn giải

Ta có IF là đường trung bình của tam giác ACD

Lại có JE là đường trung bình của tam giác BCD

Từ (1) và (2) suy ra:

Do đó IJEF là hình thoi

Suy ra (IE; JF) = 90°.

Chọn D

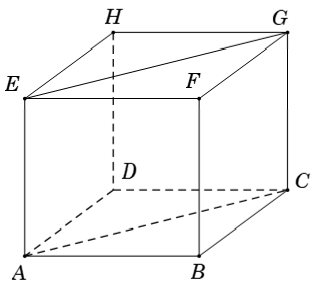
Ví dụ 5: Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ AB→ và DH→

A. 45°                        B. 90°                        C. 120°                        D.60°

Hướng dẫn giải:

Vì DH→ = AE→ ( ADHE là hình vuông) nên (AB→, DH→) = (AB→, AE→) = ∠BAE = 90° (ABFE là hình vuông).

Chọn B

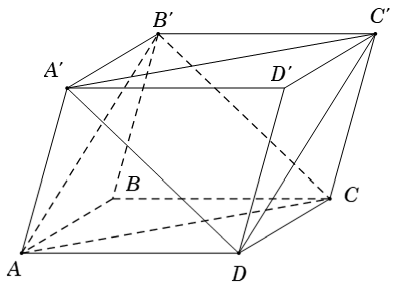
Ví dụ 6: Cho hình hộp ABCD.A’B’C’D’. Giả sử tam giác AB’C và A’DC’ đều có ba góc nhọn. Góc giữa hai đường thẳng AC và A’D là góc nào sau đây?

Hướng dẫn giải

Ta có : AC // A’C’ ( do AA’CC’ là hình bình hành) mà ∠DA'C' nhọn (do tam giác A’DC’ là tam giác nhọn) nên :

(AC, A'D) = (A'C', A'D) = ∠DA'C'

Chọn B

Ví dụ 7: Cho hình lập phương ABCD.A’B’C’D’. Chọn khẳng định sai?

A. Góc giữa AC và B’D’ bằng 90°

B. Góc giữa B’D’ và AA’ bằng 60°

C. Góc giữa AD và B’C bằng 45°

D. Góc giữa BD và A’C’ bằng 90°.

Hướng dẫn giải

Ta có (AA', B'D') = (BB', B'D') = ∠BB'C = 90°.

Khẳng định B sai. Chọn B.

Ví dụ 8: Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ AB→ và EG→?

A. 90°               B. 60°               C. 45°               D. 120°

Hướng dẫn giải

Vì EG→ = AC→ ( tứ giác AEGC là hình chữ nhật) nên:

 (do ABCD là hình vuông)

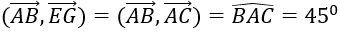
Chọn C.

C. Bài tập vận dụng

Câu 1: Cho hình chóp S.ABC có SA = SB và CA = CB. Tính số đo của góc giữa hai đường thẳng chéo nhau SC và AB

A. 30°                 B. 45°                 C. 60°                 D. 90°

Câu 2: Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Khi đó cos( AB; DM) bằng

Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo của góc (MN; SC) bằng

A. 30°                 B. 45°                 C. 60°                 D.90°

Câu 4: Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng:

A. 60°                 B. 30°                 C. 90°                 D. 45°

Câu 5: Cho tứ diện ABCD đều cạnh bằng a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa AO và CD bằng bao nhiêu?

A. 0°                 B. 30°                 C. 90°                 D. 60°

Câu 6: Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ; CD)bằng:

A . 90°                 B. 45°                 C. 30°                 D. 60°

Câu 7: Cho hình chóp S.ABCD có cạnh SA = x, tất cả các cạnh còn lại đều bằng a. Tính số đo của góc giữa hai đường thẳng SA và SC

A. 30°                 B. 45°                 C. 60°                 D.90°

Câu 8: Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD bằng:

A. 60°                 B. 30°                 C. 90°                 D. 45°

Câu 9: Cho tứ diện ABCD đều cạnh bằng a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa AO và CD bằng bao nhiêu?

A. 0°                 B. 30°                 C. 90°                 D. 60°