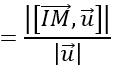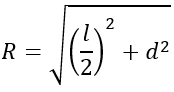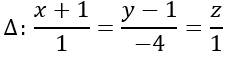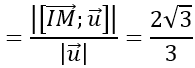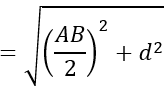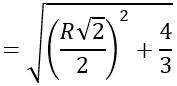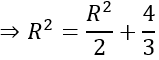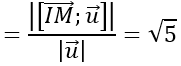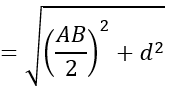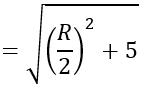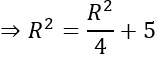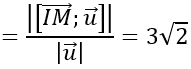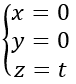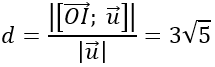Viết phương trình mặt cầu tâm I cắt đường thẳng theo dây cung có độ dài l 

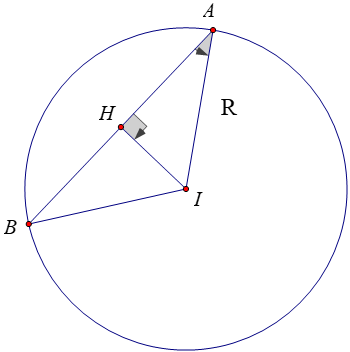
Phương pháp giải

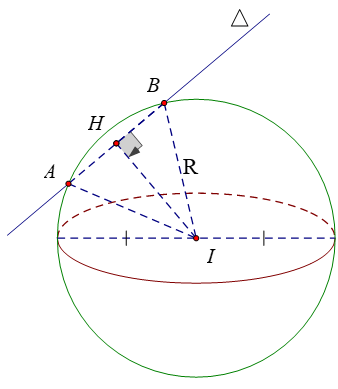
Độ dài dây cung l=AB

+ Khoảng cách từ I đến đường thẳng Δ là:

d=d(I;(Δ))

trong đó M là điểm thuộc Δ, u→ là VTCP của ∆

+ Gọi R là bán kính của mặt cầu

Ví dụ minh họa

Bài 1: Viết phương trình mặt cầu (S) có tâm I (2; 3; -1) và cắt đường thẳng

tại 2 điểm A, B với AB = 16

Hướng dẫn:

Chọn M (-1; 1; 0) ∈ Δ

⇒ IM→=(3;2; 1)

Đường thẳng Δ có một vecto chỉ phương là u→=(1; -4;1)

Ta có: [IM→ ; u→ ]=(2;4;14)

⇒ d(I,Δ)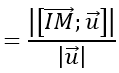= 2√3

Gọi R là bán kính mặt cầu

Ta có:

R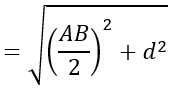= 2√(19)

Vậy phương trình mặt cầu là:

(x-2)²+(y-3)²+(z+1)²=76

Bài 2: Cho điểm I (0; 0; 3) và đường thẳng 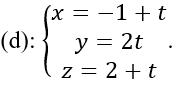Viết phương trình mặt cầu (S) có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB vuông

Hướng dẫn:

Điểm M (-1; 0; 2) ∈d

⇒ IM→=(-1;0; -1)

Đường thẳng Δ có một vecto chỉ phương là u→=(1; 2;1)

Ta có: [IM→ ; u→ ]=(2;0;-2)

⇒ d(I,Δ)

+ Do tam giác IAB cân tại I nên IAB sẽ vuông cân tại I có IA=R

⇒ AB= R√2

Ta có:

R

⇒ R²=8/3

Phương trình mặt cầu cần tìm là:

x² +y²+ (z-3)²=8/3

Bài 3: Cho điểm I (1; 0; 0) và đường thẳng 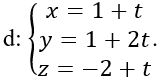Viết phương trình mặt cầu (S) có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB đều:

Hướng dẫn:

Điểm M (1; 1; -2) ∈d

⇒ IM→=(0;1; -2)

Đường thẳng Δ có một vecto chỉ phương là u→=(1; 2;1)

Ta có: [IM→ ; u→ ]=(5;-2;-1)

⇒ d(I,Δ)

+ Tam giác IAB đều cạnh R

⇒ AB=R

Ta có:

R

⇒ R² =20/3

Phương trình mặt cầu cần tìm là:

(x-1)² +y² +z²=20/3

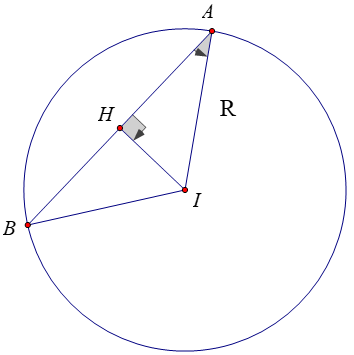
Bài 4: Cho điểm I (1; 1; -2) và đường thẳng 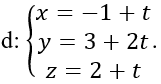Viết phương trình mặt cầu (S) có tâm I và cắt đường thẳng d tại 2 điểm A, B sao cho IABˆ=30⁰

Hướng dẫn:

Gọi H là chân đường vuông góc của I trên AB

Xét tam giác AHI vuông tại H, AI = R có:

IH=AI.sin⁡(IABˆ)=R.sin⁡(30⁰⁾=R/2

Điểm M (-1; 3; 2) ∈d

⇒ IM→=(-2;2; 4)

Đường thẳng Δ có một vecto chỉ phương là u→=(1; 2;1)

Ta có: [IM→ ; u→ ]=(-6;6;-6)

⇒ d(I,Δ)

Ta có: IH = d(I,Δ)

⇒ R/2=3√2 ⇒ R=6√2

Vậy phương trình mặt cầu cần tìm là:

(x-1)² +(y-1)² +(z+2)²=72

Bài 5: Viết phương trình mặt cầu có tâm I (3; 6; -4) và cắt trục Oz tại 2 điểm A, B sao cho diện tích tam giác IAB bằng 6√5

Hướng dẫn:

Phương trình đường thẳng Oz là : 

Điểm O(0; 0; 0) thuộc Oz ⇒ OI→=(3;6; -4)

Một vecto chỉ phương của Oz là u→= (0; 0; 1)

⇒ [OI→ ; u→ ]=(6; -3;0)

Khoảng cách từ I đến trục Oz là:

Ta có: S_IAB=1/2 IH .AB=1/2 .3√5 .AB=6√5 ⇒ AB=4

Gọi R là bán kính mặt cầu

⇒ R²=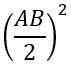+d²=2²+45=49

Vậy phương trình mặt cầu cần tìm là:

(x-3)² +(y-6)² +(z+4)²=49