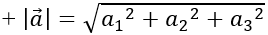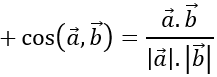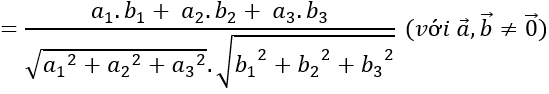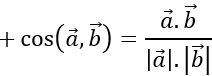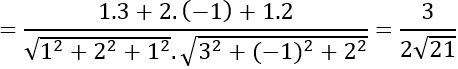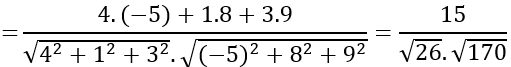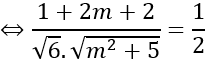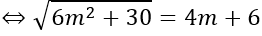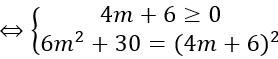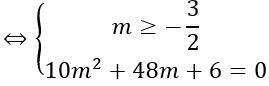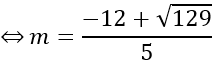Công thức tính Tích vô hướng của hai vecto trong không gian chi tiết
Với Công thức tính Tích vô hướng của hai vecto trong không gian Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Công thức tính Tích vô hướng của hai vecto trong không gian.
Công thức tính Tích vô hướng của hai vecto trong không gian
Phương pháp giải & Ví dụ
+ Tích vô hướng của hai vecto:
a→.b→=a1.b1+ a2.b2+ a3.b3
+ a→⊥b→⇔a1.b1+ a2.b2+ a3.b3=0
+ a→2=a12+a22+a32

Ví dụ minh họa
Bài 1: Trong không gian với hệ trục tọa độ Oxyz, cho các vecto a→=(1;2;1),
b→=(3;-1;2), c→=(4; -1; -3),d→=(3; -3; -5),u→=(1;m;2),m∈R.
a) Tính a→.b→; b→(a→-2c→)
b) So sánh a→.(b→.c→) và (a→.b→ ) c→
c) Tính các góc (a→,b→ ), ( a→+b→,3a→- 2c→ )
d) Tìm m để u→⊥(b→+d→)
e) Tìm m để (u→,a→ )=600
Hướng dẫn:
a) a→ =(1;2;1),b→ =(3;-1;2)
⇒a→ .b→ =1.3+2.(-1)+1.2=3.
c→ =(4; -1; -3)⇒2c→ =(8; -2; -6)⇒ a→ -2c→ =(-7;4;7)
⇒b→ (a→ -2c→ )=3.(-7)-1.4+2.7=-11
b) b→ .c→ =3.4+(-1).(-1)+2.(-3)=7⇒a→ .(b→ .c→ )=(7;14;7)
a→ .b→ =3⇒(a→ .b→ ) c→ =(12; -3; -9)
Vậy a→ .(b→ .c→ )≠(a→ .b→ ) c→
c) Ta có:
⇒(a→.b→ )≈710
+ a→+ b→=(4;1;3),3a→- 2c→=(-5;8;9)
⇒cos( a→+b→,3a→- 2c→ )
⇒( a→ +b→ ,3a→ - 2c→ )≈770
d) b→ +d→ =(6; -4; -3); u→ =(1;m;2)
u ⃗⊥(b→ +d ⃗ )⇔u→ .(b→ +d→ )=0⇔6-4m-6=0⇔m=0
e)
(u→ ,a→ )=600⇔cos(u→ ,a→ )=1/2
Bài 2: Trong không gian hệ tọa độ Oxyz, cho hai vecto a→,b→ sao cho (a→,b→ )=1200,
|a→ |=2; |b→ |=3. Tính |a→+ b→ | và |a→-2b→ |
Hướng dẫn:
Áp dụng công thức: a→ .b→ =|a→ |.|b→ |.cos(a→ ,b→ )
Ta có: |a→ + b→ |2=(a→ + b→ )2=a→ 2+2a→ .b→ +b→ 2
=|a→ |2+|b→ |2+2|a→ |.|b→ |.cos(a→ ,b→ )=4+9+2.2.3.((-1)/2)=7
⇒|a→ + b→ |=√7
Tương tự:
|a→ -2b→ |2 =|a→ |2+4|b→ |2-4|a→ |.|b→ |.cos(a→ ,b→ )=4+36-4.2.3.((-1)/2)=52
⇒|a→ -2b→ |=2√(13)