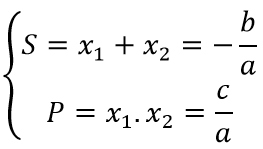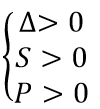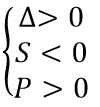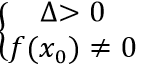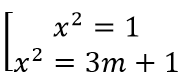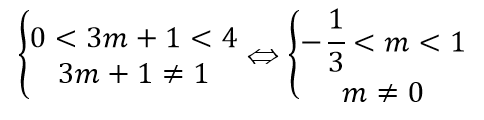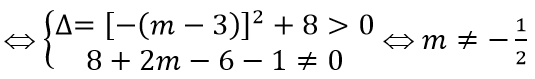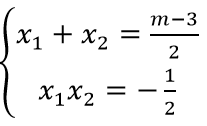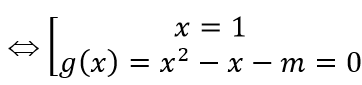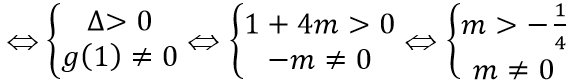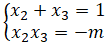Tìm m để giao điểm của hai đồ thị thoả mãn điều kiện

A. Phương pháp giải & Ví dụ

- Về phương trình

Phương trình bậc hai y = ax² + bx + c(a ≠ 0)

- Định lí Viette: Nếu phương trình có hai nghiệm x₁ , x₂ thì ta có:

   - Phương trình có hai nghiệm trái dấu khi và chỉ khi P < 0

   - Phương trình có hai nghiệm dương phân biệt khi và chỉ khi 

   - Phương trình có hai nghiệm âm phân biệt khi và chỉ khi 

   - Phương trình có hai nghiệm phân biệt khác x_o khi và chỉ khi 

   - Các công thức cần nhớ

Độ dài đoạn thẳng nối hai điểm: Với 2 điểm A(x₁ , y₁) và B(x₂ , y₂) tùy ý ta có:

AB=√((x₂ -x₁ )² +(y₂ - y₁)² )

Khoảng cách từ một điểm đến một đường thẳng cho trước: Khoảng cách từ điểm M(x_o , y_o) đến đường thẳng Δ: Ax + By + C = 0 được tính theo công thức

d(M,Δ)= |Ax_o + By_o + C|/√(A² + B² )

Diện tích tam giác: Trong một tam giác bất kỳ, ta có:

S = (1/2)ah_a = (1/2)bh_b = (1/2)ch_c = abc/4R = pr

Trong đó:

    a,b,c là độ dài ba cạnh của tam giác và p = (a + b + c)/2 là nửa chu vi.

    h_a, h_b, h_c là độ dài của đường cao tương ứng với các cạnh a,b,c.

    R,r lần lượt là bán kính của các đường tròn ngoại và nội tiếp tam giác.

    Phương trình đường thẳng Δ đi qua A(a; b) và có hệ số góc k cho trước có dạng y = k(x - a) + b

Ví dụ minh họa

Ví dụ 1: Cho hàm số y = x⁴ - (3m + 2)x² + 3m (m là tham số) có đồ thị (C_m). Tìm m để đường thẳng d:y=-1 cắt đồ thị hàm số tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2.

Hướng dẫn:

Phương trình hoành độ giao điểm của (C_m) và đường thẳng d

x⁴ - (3m + 2)x² + 3m = -1 ⇔ x⁴ - (3m + 2)x² + 3m + 1 = 0 ⇔ 

Để d cắt (C_m) tại bốn điểm phân biệt có hoành độ nhỏ hơn 2 khi và chỉ khi

Vậy tập hợp các giá trị của tham số m cần tìm là m = (-1/3; 1)\\{0}

Ví dụ 2: Cho đồ thị (C):y = (mx - 1)/(x + 2) và đường thẳng d: y = 2x - 1. Xác định giá trị của tham số m để (C) cắt d tại hai điểm phân biệt A, B sao cho AB=√10

Hướng dẫn:

Phương trình hoành độ giao điểm (mx - 1)/(x + 2) = 2x - 1 (1)

Điều kiện x ≠ -2

Khi đó (1) ⇔ mx - 1 = (2x - 1)(x + 2)

⇔ 2x² - (m - 3)x - 1 = 0 (2)

(d) cắt (C_m) tại hai điểm phân biệt A, B ⇔ (1) có hai nghiệm phân biệt

⇔ (2) có hai nghiệm phân biệt khác -2

Đặt A(x₁ ; 2x₁ - 1); B(x₂ ; 2x₂ - 1) với x₁ ,x₂ là hai nghiệm của phương trình (2)

Theo định lí Vi ét ta có 

Khi đó AB = √((x₁ - x₂)² + 4(x₁ - x₂)² ) = √10 ⇔ 5[(x₁ + x₂ )² - 4x₁ x₂ ] = 10

⇔ ((m - 3)/2)² + 2 = 2

⇔ m = 3 (thỏa mãn)

Vậy giá trị cần tìm là m = 3

Ví dụ 3: Cho hàm số y = x³ - 2x² + (1 - m)x + m có đồ thị (C_m). Xác định tất cả các giá trị của tham số m để (C_m) cắt trục Ox tại ba điểm phân biệt có hoành độ x₁ ,x₂ ,x³ thỏa mãn x₁² +x₂² +x³² =4.

Hướng dẫn:

Phương trình hoành độ giao điểm của (C) và đường thẳng d:

x³ - 2x² +(1 - m)x + m = 0 ⇔ (x - 1)(x² - x - m) = 0

(C_m) cắt Ox tại ba điểm phân biệt ⇔ phương trình g(x) = 0 có hai nghiệm phân biệt khác 1

Gọi x₁ = 1 còn x₂ ,x³ là nghiệm phương trình g(x) = 0 nên theo Viet ta có 

Vậy x₁² + x₂² + x³² = 4 ⇔ 1+(x₂ +x³)² -2x₂ x³=4

⇔ 1 + 1² + 2m = 4 ⇔ 2m - 2 = 0 ⇔ m = 1