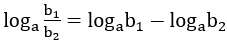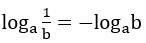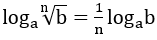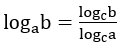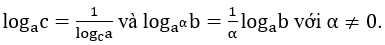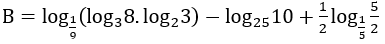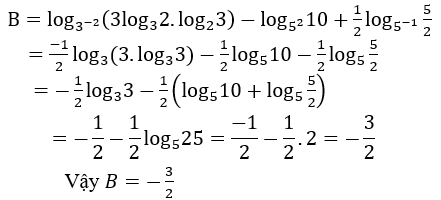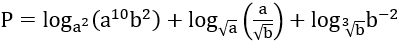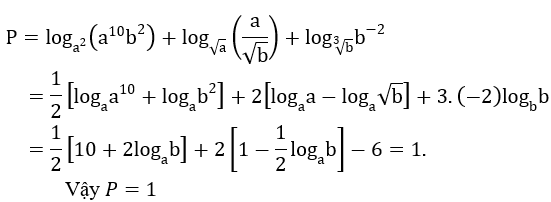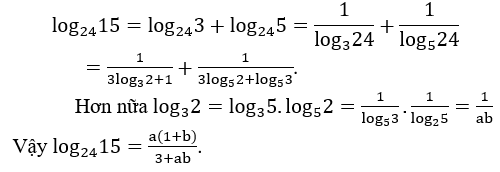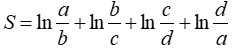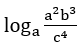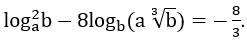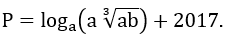Cách giải bài tập về Lôgarit cực hay

A. Phương pháp giải & Ví dụ

1. Định nghĩa:

Cho hai số dương a,b với a ≠ 1. Số α thỏa mãn đẳng thức a^α = b được gọi là lôgarit cơ số a của b và kí hiệu là log_ab . Ta viết: α = log_ab ⇔ a^α = b.

2. Các tính chất: Cho a, b > 0, a ≠ 1, ta có:

    • log_aa = 1, log_a1 = 0

    • a^log_ab = b, log_a(a^α) = α

3. Lôgarit của một tích: Cho 3 số dương a, b₁, b₂ với a ≠ 1, ta có

    • log_a(b₁.b₂) = log_ab₁ + log_ab₂

4. Lôgarit của một thương: Cho 3 số dương a,b₁, b₂ với a ≠ 1, ta có

    • 

    • Đặc biệt : với a, b > 0, a ≠ 1 ⇒ 

5. Lôgarit của lũy thừa: Cho a,b > 0, a ≠ 1, với mọi α, ta có

    • log_ab^α = αlog_ab

    • Đặc biệt: 

6. Công thức đổi cơ số: Cho 3 số dương a, b, c với a ≠ 1, c ≠ 1, ta có

    • 

    • Đặc biệt : 

    Lôgarit thập phân và Lôgarit tự nhiên

        ♦ Lôgarit thập phân là lôgarit cơ số 10. Viết : log₁₀b = logb = lgb

        ♦ Lôgarit tự nhiên là lôgarit cơ số e. Viết : log_eb = lnb

Ví dụ minh họa

Bài 1: Rút gọn biểu thức B

Hướng dẫn:

Bài 2: Tính giá trị của biểu thức P (với 0 < a ≠ 1; 0 < b ≠ 1).

Hướng dẫn:

Bài 3: Tính log₂₄15 theo a, b , biết log₂5 = a, log₅3 = b.

Hướng dẫn:

B. Bài tập vận dụng

Bài 1: Cho các số dương a, b, c, d. Tính giá trị của biểu thức

Bài 2: Cho a,b > 0 và a, b ≠ 1, biểu thức 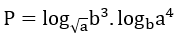 có giá trị bằng bao nhiêu?

Bài 3: Cho số thực x thỏa mãn: 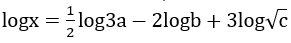 (a, b, c là các số thực dương). Hãy biểu diễn x theo a, b, c.

Bài 4: Biết log_ab=2, log_ac = -3. Tính giá trị của biểu thức 

Bài 5: Cho a, b là hai số thực dương khác 1 và thỏa mãn 

Tính giá trị biểu thức 

Bài 6: Tính log₃₆24, biết log₁₂27 = a

Bài 7: Tính log₂₅24 theo a, b, biết log₆15 = a, log₁₂18 = b

Bài 8: Tính log₁₂₆150 theo a, b, c, biết log₂3 = a, log₃5 = b, log₅7 = c.