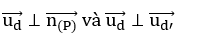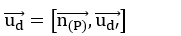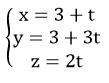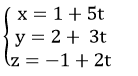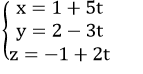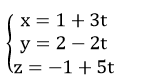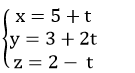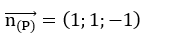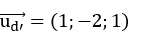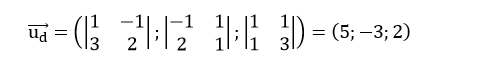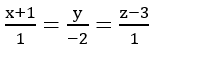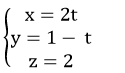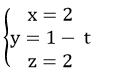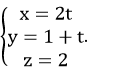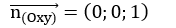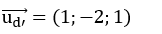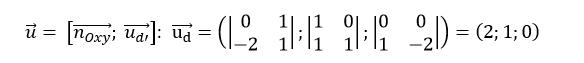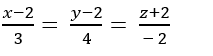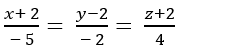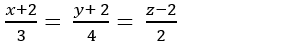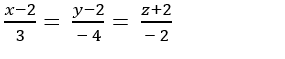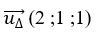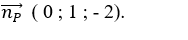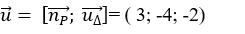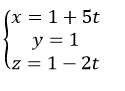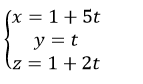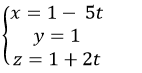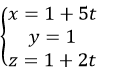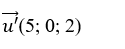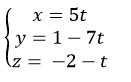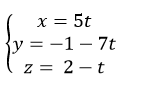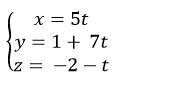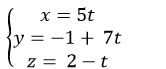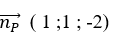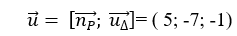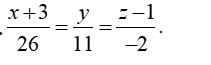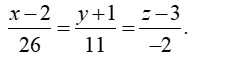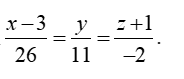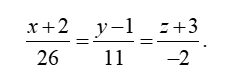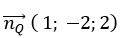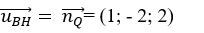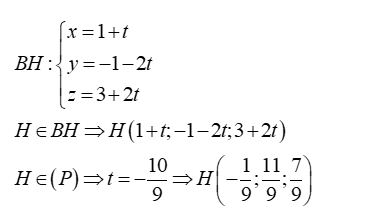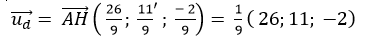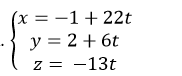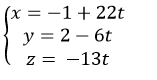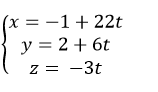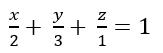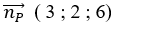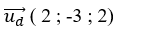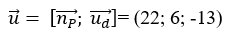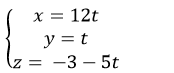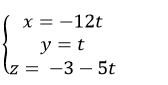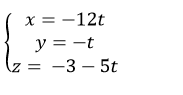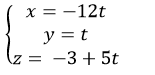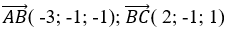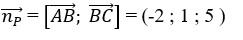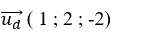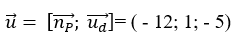Viết phương trình đường thẳng đi qua 1 điểm, song song với mặt phẳng và vuông góc với đường thẳng

A. Phương pháp giải

Do đường thẳng song song với mặt phẳng ( P) và vuông góc với đường thẳng d’ nên

Suy ra 

Mà d’ không vuông góc với (P)

=>Véc tơ chỉ phương của d là 

+ Đường thẳng d đi qua điểm M( đã biết) và nhận vecto u_d→ làm vecto chỉ phương

=> phương trình tham số và phương trình chính tắc của đường thẳng d.

B. Ví dụ minh họa

Ví dụ 1. Viết phương trình đường thẳng d đi qua điểm M (1; 2; -1), song song với mặt phẳng (P): x + y – z = 3 và vuông góc với đường thẳng d’:

A.

B.

C.

D.

Hướng dẫn giải

Vecto pháp tuyến của mặt phẳng (P) là: 

Vecto chỉ phương của đường thẳng d’ là: 

Do đường thẳng d song song với mặt phẳng (P) và vuông góc với đường thẳng d’ nên một vecto chỉ phương của đường thẳng d là: 

d đi qua điểm M (1; 2; -1)

Vậy phương trình đường thẳng d là 

Chọn B.

Ví dụ 2: Viết phương trình đường thẳng d đi qua điểm M (0; 1; 2), song song với mặt phẳng (Oxy) và vuông góc với đường thẳng d':

A .

B.

C.

D. Đáp án khác

Hướng dẫn giải

Phương trình mặt phẳng ( Oxy) là: z= 0; vecto pháp tuyến của mặt phẳng này là: 

Vecto chỉ phương của đường thẳng d’ là: 

Do đường thẳng d song song với mặt phẳng (Oxy) và vuông góc với đường thẳng d’ nên một vecto chỉ phương của đường thẳng d là:

d đi qua điểm M (0; 1; 2)

Vậy phương trình đường thẳng d là 

Chọn C.

Ví dụ 3 : Trong không gian với hệ tọa độ Oxyz ; cho mặt phẳng (P) : y- 2z- 1= 0 và đường thẳng Δ : 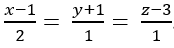 . Phương trình chính tắc đường thẳng d đi qua điểm B( 2 ; 2 ; - 2) song song với (P) và vuông góc với Δ là

A.

B.

C.

D.

Hướng dẫn giải

Đường thẳng Δ có vectơ chỉ phương 

Mặt phẳng (P) có vectơ pháp tuyến 

Gọi u_d→ là vectơ chỉ phương của d.

Do đường thẳng d song song với mặt phẳng (P) và vuông góc với đường thẳng Δ nên một vecto chỉ phương của đường thẳng d là: 

Vậy phương trình chính tắc của d là: 

Chọn D.

Ví dụ 4: Trong không gian với hệ tọa độ Oxyz; cho mặt phẳng (P): 2x+ y- 5z+ 1= 0. Phương trình đường thẳng d đi qua điểm A (1;1;1) song song với ( P) và vuông góc với trục tung là

A.

B.

C.

D.

Hướng dẫn giải

Trục tung Oy có vectơ chỉ phương  .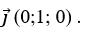

Mặt phẳng (P) có vectơ pháp tuyến  .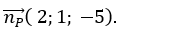

Do đường thẳng d song song với mặt phẳng (P) và vuông góc với trục tung nên một vecto chỉ phương của đường thẳng d là:  .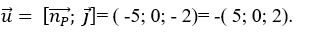

Đường thẳng d đi qua điểm A( 1; 1; 1) và có vectơ chỉ phương là 

Vậy phương trình của d là: 

Chọn D.

Ví dụ 5: Trong không gian với hệ tọa độ Oxyz; cho mặt cầu (S): x² +(y-1)² +(z+ 2)² = 4. Phương trình đường thẳng d đi qua tâm của mặt cầu (S), song song với mặt phẳng (P): x+ y- 2z= 0 và vuông góc với đường thẳng Δ: 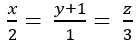 là.

A.

B.

C.

D.

Hướng dẫn giải

+ Tâm của mặt cầu ( S) là I( 0 ;1 ; -2) .

+ Đường thẳng Δ có vectơ chỉ phương  .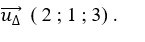

+ Mặt phẳng ( P) có vectơ pháp tuyến 

+ Đường thẳng d đi qua điểm I( 0 ; 1 ; -2) và có vectơ chỉ phương là :

Vậy phương trình của d là 

Chọn A.

Ví dụ 6: Trong không gian với hệ tọa độ Oxyz; cho mặt phẳng (P): x- 2y+ 2z- 5= 0 và hai điểm A(-3; 0; 1); B( 1; -1; 3). Trong các đường thẳng đi qua A và song song với (P), đường thẳng mà khoảng cách từ B đến đường thẳng đó là nhỏ nhất có phương trình là.

A.

B.

C.

D.

Hướng dẫn giải

Gọi d là đường thẳng cần tìm

+ Gọi mặt phẳng (Q) qua A( -3; 0;1) và song song với (P).

Khi đó: (Q) có dạng: x- 2y+ 2z + D= 0

Thay tọa độ điểm A vào phương trình ( Q) ta được : -3- 2.0+ 2.1+ D= 0 ⇔ D = 1

Vậy phương trình ( Q): x- 2y + 2z +1= 0

+ Gọi K; H lần lượt là hình chiếu của B lên d; (Q).

Ta có: d( B; d) = BK ≥BH

Do đó AH là đường thẳng cần tìm.

+ Mặt phẳng ( Q) có vectơ pháp tuyến 

BH qua B và có vectơ chỉ phương 

=> Phương trình đường thẳng BH là:

+ Đường thẳng d đi qua điểm A( -3; 0; 1) và có vectơ chỉ phương 

Vậy phương trình của d là

Chọn A.

Ví dụ 7: Trong không gian với hệ trục tọa độ Oxyz; cho mặt phẳng (P) đi qua ba điểm A( 2; 0; 0); B( 0; 3; 0) và C( 0; 0; 1); đường thẳng d: . Viết phương trình đường thẳng Δ đi qua M (-1; 2; 0)song song với mặt phẳng (P) và vuông góc với đường thẳng d.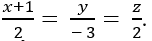

A.

B.

C.

D. Đáp án khác

Hướng dẫn giải

+ Phương trình đoạn chắn mặt phẳng ( P):

Mặt phẳng (P) có vectơ pháp tuyến 

+ Đường thẳng d có vecto chỉ phương 

+ Đường thẳng Δ đi qua điểm M(-1 ; 2 ; 0) và có vectơ chỉ phương là :

Vậy phương trình của Δ là 

Chọn A.

Ví dụ 8: Trong không gian với hệ trục tọa độ Oxyz; cho mặt phẳng (P) đi qua ba điểm A( 1; 2; 1); B( -2; 1; 0) và C( 0; 0; 1) . Đường thẳng d có phương trình : 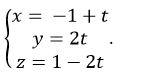 . Viết phương trình đường thẳng Δ đi qua M( 0; 0; -3) và song song với (P); vuông góc với đường thẳng d.

A.

B.

C.

D.

Hướng dẫn giải

+ Ta tìm vecto pháp tuyến của mặt phẳng ( P)

Ta có: 

Mặt phẳng (P) có vectơ pháp tuyến 

+ Đường thẳng d có vecto chỉ phương 

+ Đường thẳng Δ đi qua điểm M( 0; 0; - 3) và có vectơ chỉ phương là :

Vậy phương trình của Δ là 

Chọn B.