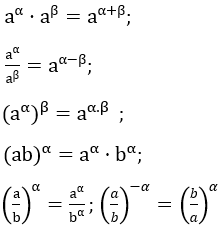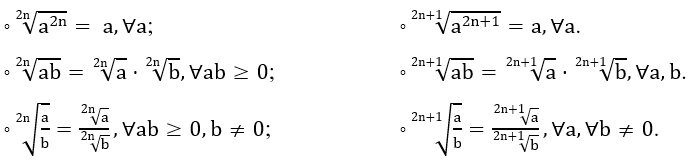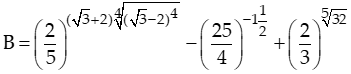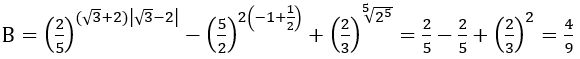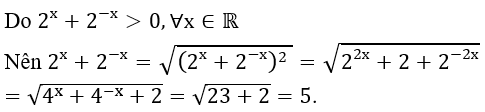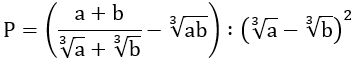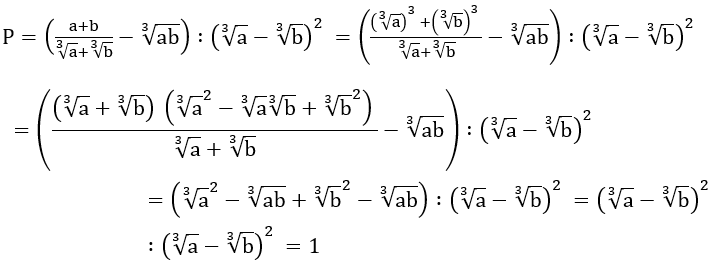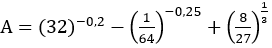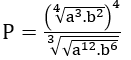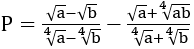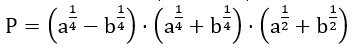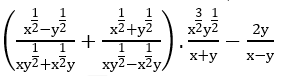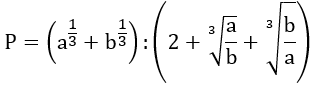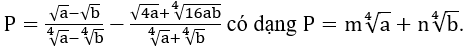Cách giải bài tập về Lũy thừa chi tiết
Với Cách giải bài tập về Lũy thừa Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Cách giải bài tập về Lũy thừa .
Cách giải bài tập về Lũy thừa cực hay
A. Phương pháp giải & Ví dụ
• Cho số thực b và số nguyên dương n (n ≥ 2). Số a được gọi là căn bậc n của số b nếu an = b.
• Chú ý:
| Số mũ α | Cơ số a | Lũy thừa aα |
| α = n ∈ N* | a ∈ R | aα = an = a⋅a⋯a (n thừa số a) |
| α = 0 | a ≠ 0 | aα = a0 = 1 |
| α = -n, (n ∈ N*) | a ≠ 0 |  |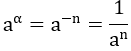
| α = m/n,(m ∈ Z, n ∈ N*) | a > 0 |  |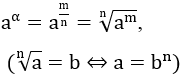
| α = limrn, (rn ∈ Q,n ∈ N*) | a > 0 | aα = limarn |
2. Một số tính chất của lũy thừa
• Giả thuyết rằng mỗi biểu thức được xét đều có nghĩa:
• Nếu a > 1 thì aα > aβ ⇔ α > β; Nếu 0 < a < 1 thì aα > aβ ⇔ α < β.
• Với mọi 0 > a < b, ta có: am < bm ⇔ m > 0; am > bm ⇔ m < 0
• Chú ý:
◦ Các tính chất trên đúng trong trường hợp số mũ nguyên hoặc không nguyên.
◦ Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số a phải khác 0.
◦ Khi xét lũy thừa với số mũ không nguyên thì cơ số a phải dương.
3. Một số tính chất của căn bậc n
• Với a,b ∈ R;n ∈ N*, ta có:
• Với a,b ∈ R, ta có:
Ví dụ minh họa
Bài 1: Tính giá trị của biểu thức
Hướng dẫn:
Bài 2: Biết 4x + 4-x = 23 tính giá trị của biểu thức P = 2x + 2-x :
Hướng dẫn:
Bài 3: Cho các số thực dương a và b. Thu gọn biểu thức
Hướng dẫn:
B. Bài tập vận dụng
Bài 1: Cho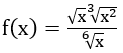 
khi đó giá trị của biểu thức f(1,3) bằng bao nhiêu?
Bài 2: Tính giá trị của biểu thức sau:
Bài 3: Cho a,b là các số dương. Rút gọn biểu thức
Bài 4: Cho các số thực dương a và b. Rút gọn biểu thức
Bài 5: Cho a > 0 , b > 0. Thu gọn biểu thức
Bài 6: Rút gọn biểu thức
Bài 7: Cho các số thực dương a và b. Biểu thức thu gọn của biểu thức
Bài 8: Cho các số thực dương phân biệt a và b. Biểu thức thu gọn của biểu thức. Tìm m và n
