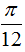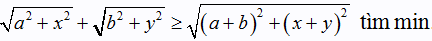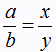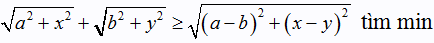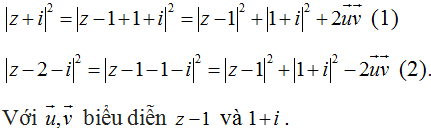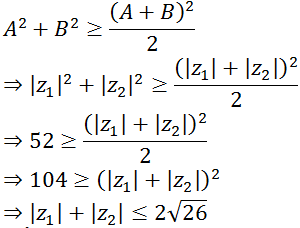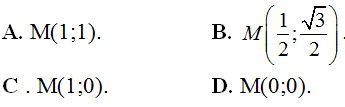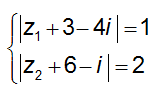Tìm giá trị nhỏ nhất, lớn nhất của số phức (Dạng 1)

Cho số phức z thỏa mãn |z - (a + bi)| = c, (c > 0), tìm giá trị nhỏ nhất, giá trị lớn nhất của P với P = |z + z₃| + |z + z₄| hoặc P chứa z², z³ (sử dụng các hằng đẳng thức đáng nhớ)

1. Phương pháp

Cách 1: PP lượng giác hóa

Vì tọa độ điểm biểu diễn là đường tròn nên đưa về dạng X² + Y² = 1

(Có thể sử dụng trong trường hợp tọa độ điểm biểu diễn là elip)

Đặt X = cosa; Y = sina

Khi đó P biểu diễn theo cosa và sina

Sử dụng MODE 7 khảo sát với START = 0; END = 2; STEP = 

(Chú ý dùng lệnh Shift Mode  5 - 1)

Cách 2: Sử dụng pp BĐT

BĐT Bunhia Copski: (Ax + By)² ≤ (A² + B²)(x² + y²) tìm max

BĐT Mincopxki:

Dấu = xảy ra khi 

BĐT vecto:

Dấu = xảy ra khi 

2. Ví dụ minh họa

Ví dụ 1: Cho số phức z thỏa mãn |z - 1| = √2. Tìm GTLN của T = |z + i| + |z - 2 - i|

Hướng dẫn:

Ta có:

Cộng (1) với (2) ta được:

|z + i|² + |z - 2 - i|² = 2|z - 1|² + 4 = 8 (không đổi)

Áp dụng đẳng thức bunhia xcopki:

T² = (|z + i| + |z - 2 - i|)² ≤ 2(|z + i|² + |z - 2 - i|²) = 16 => T ≤ 4

Ví dụ 2: Với 2 số phức z₁, z₂ thỏa mãn z₁ + z₂ = 8 + 6i và |z₁ - z₂| = 2. Tính GTLN của P = |z₁| + |z₂|

A. 5 + 3√5    B. 2√26    C. 4√6    D. 34 + 3√2

Hướng dẫn:

CÁCH 1: Ta có:

|z₁ + z₂|² + |z₁ - z₂|² = 2(|z₁|² + |z₂|²) ⇔ 100 + 4 = 2(|z₁|² + |z₂|²) ⇔ 52 = (|z₁|² + |z₂|²)

Lại có: Áp dụng BĐT Cauchy:

CÁCH 2:

Ta có:

ÁP dụng BĐT Bunhia Copski:

(Ax + By)² ≤ (A² + B²)(x² + y²)

=> (|z₁| + |z₂|)² ≤ 2(|z₁|² + |z₂|²) = |z₁| + |z₂|² + |z₁| - |z₂|² = 104

=> |z₁| + |z₂| ≤ 2√26

Ví dụ 3: Gọi (C) là tập hợp các điểm trên mặt phẳng biểu diễn số phức z = x - 1 + yi, thỏa mãn |z| = 1 và N là điểm biểu diễn số phức z₀ = 1 - i. Tìm điểm M thuộc (C) sao cho MN có độ dài lớn nhất.

Hướng dẫn:

Ta có M(x; y) nằm trên đường tròn (C): (x - 1)² + y² = 1 tâm I(1;0)

Do N(1; -1) nằm trên đường tròn nên MN có độ dài lớn nhất khi MN là đường kính, hay I(1;0) là trung điểm của MN.

Vậy M(1; 1)

Chọn A.

Ví dụ 4: Cho hai số phức z₁, z₂ thỏa mãn :

Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức |z₁ - z₂| .

A. 18     B. 6√2     C. 6     D. 3√2

Hướng dẫn:

Ta có:

|z₁ - z₂| = |(z₁ + 3 - 4i) - (z₂ + 6 - i) + (3 + 3i) ≤ |z₁ + 2 - 4i| + |z₂ + 6 - i| + |3 + 3i| = 3 + 3√2| = max

và |z₁ - z₂| = |(z₁ + 3 - 4i) - (z₂ + 6 - i) + (3 + 3i) ≥ |3 + 3i| - |z₁ + 2 - 4i| - |z₂ + 6 - i| = 3√2 - 3 = min

Do đó tổng Giá trị lớn nhất và Giá trị nhỏ nhất là 6√2

Chọn đáp án là B.

Ví dụ 5: Gọi (C) là tập hợp các điểm trên mặt phẳng biểu diễn số phức z = x - 1 + yi thỏa mãn |z| = 1 và N là điểm biểu diễn số phức z₀ = 5 + 3i. M là một điểm thuộc (C) sao cho MN có độ dài bé nhất. Khi đó độ dài MN bé nhất bằng

A. 6     B. √34     C. 3√5    D. 4

Hướng dẫn:

Ta có: M(x; y) nằm trên đường tròn (C): (x - 1)² + y² = 1 có tâm I(1; 0) và bán kính R = 4

Do N(5, 3) nằm ngoài (C) nên MN có độ dài bé nhất khi và chỉ khi:

MN = NI - R = 5 - 1 = 4.