Viết phương trình mặt cầu có tâm I và bán kính R chi tiết
Với Viết phương trình mặt cầu có tâm I và bán kính R Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Viết phương trình mặt cầu có tâm I và bán kính R.
Viết phương trình mặt cầu có tâm I và bán kính R
Phương pháp giải
Phương trình chính tắc của mặt cầu có tâm I (a; b; c) và bán kính R là:
(S): (x-a)2+(y-b)2+(z-c)2=R2
Ví dụ minh họa
Bài 1: Viết phương trình mặt cầu có tâm I (2; 3; -1) và có bán kính R = 5.
Hướng dẫn:
Phương trình chính tắc của mặt cầu có tâm I (a; b; c) và bán kính R là:
(S): (x-a)2+(y-b)2+(z-c)2=R2
Khi đó, phương trình mặt cầu có tâm I (2; 3; -1) và có bán kính R = 5 là:
(S): (x-2)2+(y-3)2+(z+1)2=25.
Bài 2: Viết phương trình mặt cầu có đường kính AB với A (4; -3; 7), B(2; 1; 3)
Hướng dẫn:
Gọi I là trung điểm của AB
Do AB là đường kính của mặt cầu I là tâm mặt của mặt cầu.
⇒ I(3; -1;5)
Bán kính mặt cầu là:
R=IA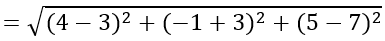
= 3
Vậy phương trình mặt cầu có đường kính AB là:
(x-3)2+(y+1)2+(z-5)2=9
Chú ý: Để lập phương trình mặt cầu nhận AB là đường kính thì ta tìm tâm I là trung điểm của AB và bán kính R=AB/2
Bài 3: Viết phương trình mặt cầu có tâm I (3; -2; 2) và đi qua A(-2; 0; -1)
Hướng dẫn:
Vì mặt cầu (S) đi qua A nên (S) có bán kính
R=IA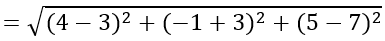=√38
Vậy phương trình mặt cầu có tâm I (3; -2; 2) và bàn kính R=√38 là:
(x-3)2+(y+2)2+(z-2)2=38
Chú ý: Để lập phương trình mặt cầu khi biết tâm I (a; b; c) và đi qua một điểm A cho trước thì ta tìm bán kính R = IA. Khi đó, phương trình mặt cầu (S) có dạng:
(S): (x-a)2+(y-b)2+(z-c)2=R2
Bài viết liên quan
- Chứng minh hai vecto cùng phương, không cùng phương chi tiết
- Cách tìm tâm và bán kính mặt cầu chi tiết
- Viết phương trình mặt cầu có tâm tiếp xúc mặt phẳng chi tiết
- Viết phương trình mặt phẳng đi qua 1 điểm và có vecto pháp tuyến chi tiết
- Viết phương trình mặt phẳng đi qua 1 điểm và song song với mặt phẳng chi tiết
