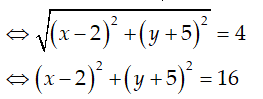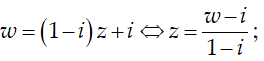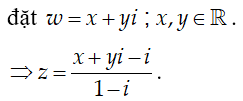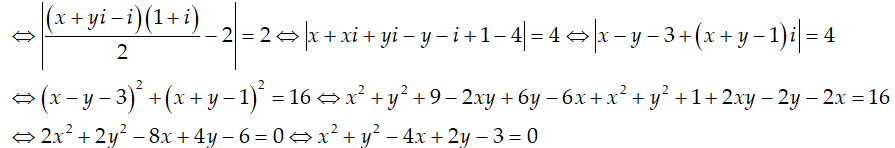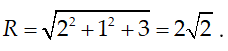Tập hợp điểm biểu diễn số phức là đường tròn chi tiết
Với Tập hợp điểm biểu diễn số phức là đường tròn Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Tập hợp điểm biểu diễn số phức là đường tròn.
Tập hợp điểm biểu diễn số phức là đường tròn
Ví dụ 1: Tập hợp các điểm M biểu diễn số phức |z -2 + 5i| = 4 thoả mãn là:
A. Đường tròn tâm I(2 ; -5) và bán kính bằng 2.
B. Đường tròn tâm I(-2 ; 5) và bán kính bằng 4.
C. Đường tròn tâm I(2 ; -5) và bán kính bằng 4.
D. Đường tròn tâm O và bán kính bằng 2.
Hướng dẫn:
.Gọi số phức z = x + yi
|z -2 + 5i| = 4 <=> |x - 2 + (y + 5)i| = 4
Vậy tập hợp điểm biểu diễn số phức là đường tròn tâm I(2; -5) bán kính R = 4.
Chọn C.

Ví dụ 2: Cho số phức z thỏa mãn |z - 2| = 2 . Biết rằng tập hợp các điểm biểu diễn các số phức w = (1-i)z + i là một đường tròn. Tính bán kính r của đường tròn đó
A.2√2 B.r = 4 C.r = √2 D.r = 2
Hướng dẫn:
Ta có:
Ta có:
Đường tròn có bán kính là
Chọn A.
Ví dụ 3:Cho số phức z thỏa mãn |z -1| = 2 ; w = (1 + √3i)z + 2 .Tập hợp điểm biểu diễn của số phức w là đường tròn, tính bán kính đường tròn đó
A. R = 3 B. R = 2 C. R = 4 D. R = 5 .
Hướng dẫn:
w = (1 + √3i)z + 2 <=> w = (1 + √3i)(z -1) + 1 + √3i + 2
<=> w - (3 + √3i) = (1 + √3i)(z-1)
=> |w - (3 + √3i) | = | (1 + √3i)(z-1)| = |(1 + √3i)| |(z-1)| = 4
Chọn C.