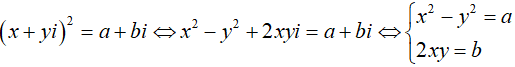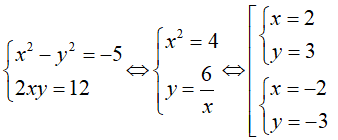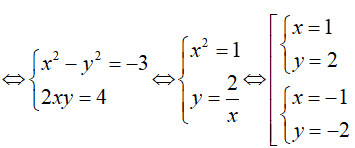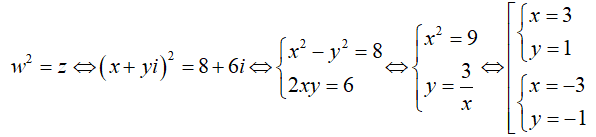Cách tìm căn bậc hai của số phức chi tiết
Với Cách tìm căn bậc hai của số phức Toán lớp 12 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải chi tiết giúp học sinh biết Cách tìm căn bậc hai của số phức .
Cách tìm căn bậc hai của số phức
Phương pháp giải
Trường hợp w là số thực: Nếu a là một số thực
+a < 0 ; a có các căn bậc hai là 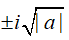
+ a = 0, a có đúng một căn bậc hai là 0.
+a > 0, acó hai căn bậc hai là 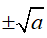
Trường hợp w = a + bi;a, b ∈ R; b ≠ 0
Gọi z = x + yi là một căn bậc hai của w khi và chỉ khi z2 = w, tức là
Mỗi cặp số thực (x; y) nghiệm đúng hệ phương trình trên cho ta một căn bậc hai x + y.i của số phức w = a + bi.

Ví dụ minh họa
Ví dụ 1:Tìm các căn bậc hai của w = -5 + 12i.
Hướng dẫn:
Gọi z = x + yi là một căn bậc hai của số phức w = -5 + 12i
Ta có z2 = w <=> (x + yi)2 = -5 + 12i
<=>
Vậy số phức w có hai căn bậc hai là 2 + 3i và -2 - 3i.
Ví dụ 2:Khai căn bậc hai số phức z = -3 + 4i có kết quả:
Hướng dẫn:
Giả sử w = x + yi là một căn bậc hai của số phức z = -3 + 4i.
Ta có:
w2 = z <=> (x + yi)2 = -3 + 4i
Do đó z có hai căn bậc hai là:
z1 = 1 + 2i
z2 = -1 - 2i
Ví dụ 3:Tính căn bậc hai của số phức z = 8 + 6i ra kết quả:
Hướng dẫn:
Giả sử w = x + yi là một căn bậc hai của số phức z = 8 + 6i.
Ta có:
Do đó z có hai căn bậc hai là
Chọn đáp án A.