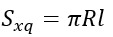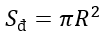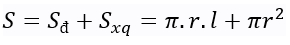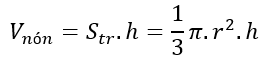Lý thuyết hình nón, khối nón

1) Mặt nón tròn xoay

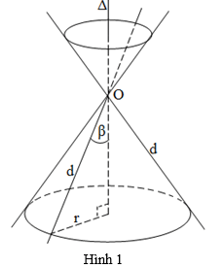
    + Trong mặt phẳng (P), cho 2 đường thẳng d, Δ cắt nhau tại O và chúng tạo thành góc β với 0 < β < 90º. Khi quay mặt phẳng (P) xung quanh trục Δ với góc β không thay đổi được gọi là mặt nón tròn xoay đỉnh O (hình 1).

    + Người ta thường gọi tắt mặt nón tròn xoay là mặt nón.

Đường thẳng Δ gọi là trục, đường thẳng d được gọi là đường sinh và góc 2β gọi là góc ở đỉnh.

2) Hình nón tròn xoay

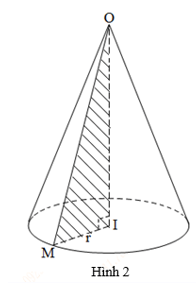
    + Cho ΔOIM vuông tại I quay quanh cạnh góc vuông OI thì đường gấp khúc OIM tạo thành một hình, gọi là hình nón tròn xoay (gọi tắt là hình nón) (hình 2).

    + Đường thẳng OI gọi là trục, O là đỉnh, OI gọi là đường cao và OM gọi là đường sinh của hình nón.

    + Hình tròn tâm I, bán kính r = IM là đáy của hình nón.

3) Công thức diện tích và thể tích của hình nón

Cho hình nón có chiều cao là h, bán kính đáy R và đường sinh là l thì có:

    + Diện tích xung quanh:

    + Diện tích đáy (hình tròn):

    + Diện tích toàn phần hình tròn:

    + Thể tích khối nón:

4) Tính chất:

- Nếu cắt mặt nón tròn xoay bởi mặt phẳng đi qua đỉnh thì có các trường hợp sau xảy ra:

    + Mặt phẳng cắt mặt nón theo 2 đường sinh thì thiết diện là tam giác cân.

    + Mặt phẳng tiếp xúc với mặt nón theo một đường sinh, trong trường hợp này, người ta gọi đó là mặt phẳng tiếp diện của mặt nón.

- Nếu cắt mặt nón tròn xoay bởi mặt phẳng không đi qua đỉnh thì có các trường hợp sau xảy ra:

    + Nếu mặt phẳng cắt vuông góc với trục hình nón thì giao tuyến là một đường tròn.

    + Nếu mặt phẳng cắt song song với 2 đường sinh hình nón thì giao tuyến là 2 nhánh của 1 hypebol.

    + Nếu mặt phẳng cắt song song với 1 đường sinh hình nón thì giao tuyến là 1 đường parabol.