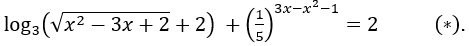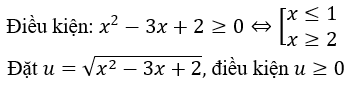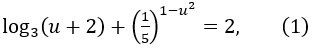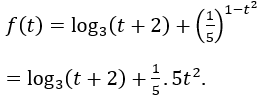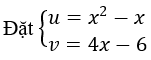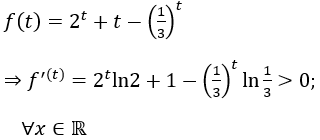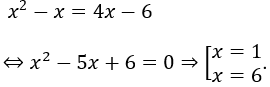Sử dụng tính đơn điệu để giải phương trình mũ

A. Phương pháp giải & Ví dụ

Hướng 1:

    • Bước 1. Chuyển phương trình về dạng f(x)=k.

    • Bước 2. Khảo sát sự biến thiên của hàm số f(x) trên D. Khẳng định hàm số đơn điệu

    • Bước 3. Nhận xét:

        + Với x = x₀ ⇔ f(x) = f(x₀) = k do đó x = x₀ là nghiệm.

        + Với x > x₀ ⇔ f(x) > f(x₀) = k do đó phương trình vô nghiệm.

        + Với x < x₀ ⇔ f(x) < f(x₀) = k do đó phương trình vô nghiệm.

    • Bước 4. Kết luận vậy x = x₀ là nghiệm duy nhất của phương trình.

Hướng 2:

    • Bước 1. Chuyển phương trình về dạng f(x) = g(x).

    • Bước 2. Khảo sát sự biến thiên của hàm số y = f(x) và y = g(x). Khẳng định hàm số y = f(x) là hàm số đồng biến còn y = g(x) là hàm số nghịch biến hoặc là hàm hằng.

    • Bước 3. Xác đinh x₀ sao cho f(x₀) = g(x₀ .

    • Bước 4. Kết luận vậy x = x₀ là nghiệm duy nhất của phương trình.

Hướng 3:

    • Bước 1. Chuyển phương trình về dạng f(u) = f(v).

    • Bước 2. Khảo sát sự biến thiên của hàm số y = f(x). Khẳng định hàm số đơn điệu.

    • Bước 3. Khi đó f(u) = f(v) ⇔ u = v.

Ví dụ minh họa

Bài 1: Giải phương trình x+2.3^log₂ x = 3 (*).

Hướng dẫn:

Ta có: (*) ⇔ 2.3^log₂x = 3-x (1).

Nhận xét:

    + Vế trái của phương trình là hàm số đồng biến.

    + Vế phải của phương trình là hàm số nghịch biến.

Do đó nếu phương trình có nghiệm thì nghiệm đó là nghiệm duy nhất.

Mặt khác: x = 1 là nghiệm của phương trình. Phương trình có nghiệm duy nhất x = 1.

Vậy tập nghiệm của phương trình là: S={1}.

Bài 2: Giải phương trình

Hướng dẫn:

⇒ x² - 3x + 2 = u² ⇒ 3x - x² - 1 = 1 - u².

Khi đó phương trình (*) có dạng

Xét hàm số:

    + Miền xác định: D = [0;+∞).

    + Đạo hàm 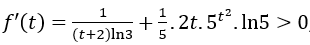 ∀x ∈ D. Suy ra hàm số đồng biến trên D.

Mặt khác f(1) = log₃ (1+2) + (1/5).5 = 2.

Do đó, phương trình (1) được viết dưới dạng

Bài 3: Giải phương trình 2^x2-x + 9^3-2x + x² + 6 = 4^2x-3 + 3^{x - x2} + 5x (*).

Hướng dẫn:

Ta có: (*) ⇔ 2^x2-x + 3^6-4x + x² + 6 = 2^4x-6 + 3^x-x2 + 5x.

        ⇔ 2^x2-x + x² - x - 3^x-x2 = 2^4x-6 + 4x - 6 - 3^6-4x.

ta được 2^u + u - 3^-u = 2^v + v - 3^-v.

Xét hàm số:

⇒ f'(t) là hàm số đồng biến trên R, mà f(u)=f(v) ⇔ u=v.

Ta có phương trình:

Vậy tập nghiệm của phương trình là: S={1;6}.